Як виконати односторонній дисперсійний аналіз у sas

Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

Цей підручник надає покроковий приклад того, як виконати односторонній дисперсійний аналіз у SAS.

Крок 1: Створіть дані

Припустімо, що дослідник набирає 30 студентів для участі в дослідженні. Для підготовки до іспиту студенти випадковим чином розподіляються для використання одного з трьох методів навчання.

Результати іспитів для кожного студента наведено нижче:

Ми можемо використати такий код, щоб створити цей набір даних у SAS:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Крок 2: Виконайте односторонній дисперсійний аналіз

Далі ми використаємо proc ANOVA для виконання одностороннього ANOVA:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
classMethod ;
modelScore = Method;
means Method / tukey cldiff ;
run ;

Примітка . Ми використали функцію середнього значення, щоб визначити, що тест Tukey слід виконувати, якщо загальне значення p від одностороннього ANOVA є статистично значущим.

Крок 3: Інтерпретація результатів

Перша таблиця, яку ми хочемо проаналізувати в результатах, це таблиця ANOVA:

З цієї таблиці ми бачимо:

• Загальне F-значення: 5,26
• Відповідне p-значення: 0,0140

Нагадаємо, що односторонній дисперсійний аналіз використовує такі нульові та альтернативні гіпотези:

• H ₀ : Усі групові середні рівні.
• H _A : Принаймні одна середня група відрізняється   відпочинок.

Оскільки p-значення таблиці ANOVA (0,0140) менше α = 0,05, ми відхиляємо нульову гіпотезу.

Це говорить нам про те, що середня оцінка іспиту не однакова для трьох методів навчання.

Пов’язане: Як інтерпретувати F-значення та P-значення в ANOVA

SAS також надає коробкові графіки для візуалізації розподілу результатів іспитів для кожного з трьох методів навчання:

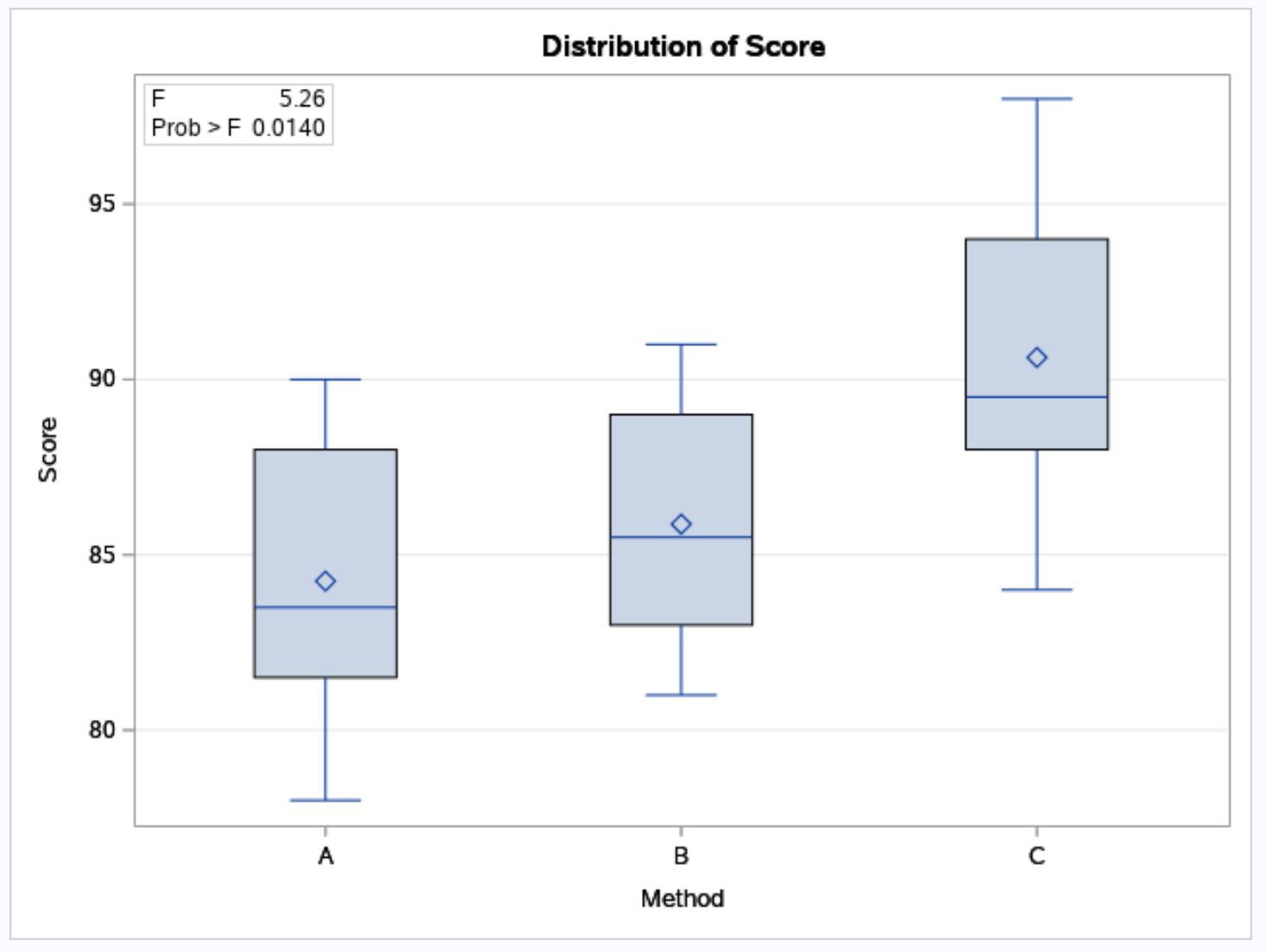
З коробкових графіків ми бачимо, що результати іспитів, як правило, вищі серед студентів, які використовували метод C, порівняно з методами B і C.

Щоб точно визначити, які групові середні відрізняються, нам потрібно звернутися до таблиці остаточних результатів, яка показує результати пост-хок тестів Тьюкі:

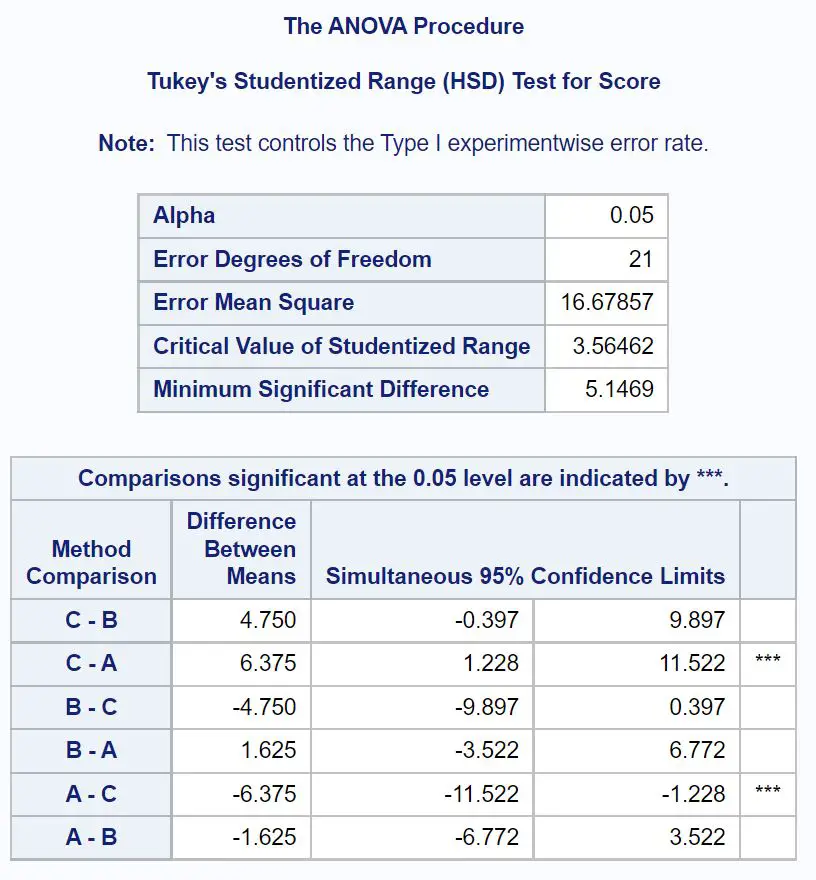
Щоб з’ясувати, які середні групи відрізняються, нам потрібно подивитися, які парні порівняння мають зірочки ( *** ).

З таблиці видно, що середні значення груп А і С статистично достовірно відрізняються.

Ми також можемо побачити 95% довірчий інтервал для різниці в середніх результатах іспиту між групами A та C:

95% довірчий інтервал для середньої різниці: [1,228, 11,522]

Крок 4: звіт про результати

Нарешті, ми можемо повідомити про результати одностороннього дисперсійного аналізу:

Для порівняння впливу трьох різних методів дослідження на результати обстеження було проведено односторонній дисперсійний аналіз.

Односторонній дисперсійний аналіз виявив наявність статистично значущої різниці в середньому іспитовому балі принаймні двох груп (F(2,21) = [5,26], p = 0,014).

Тест HSD Тьюкі для множинних порівнянь показав, що середнє значення іспитового балу суттєво відрізнялося між методами С і методами А (95% ДІ = [1,228, 11,522]).

Не було статистично значущої різниці в середніх іспитових балах між методами A та B або між методами B та C.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про односторонній дисперсійний аналіз:

Вступ до одностороннього дисперсійного аналізу
Односторонній калькулятор ANOVA
Як вручну виконати односторонній дисперсійний аналіз