Як виконати односторонній дисперсійний аналіз у spss

Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

Цей тип тесту називається одностороннім дисперсійним аналізом, оскільки ми аналізуємо вплив змінної- прогнозу на змінну відповіді.

Якби нас замість цього цікавив вплив двох змінних предикторів на змінну відповіді, ми могли б виконати двосторонній дисперсійний аналіз .

У цьому посібнику пояснюється, як виконати односторонній дисперсійний аналіз у SPSS.

Приклад: односторонній дисперсійний аналіз у SPSS

Припустімо, що дослідник набирає 30 студентів для участі в дослідженні. Студенти випадковим чином розподіляються для використання однієї з трьох методів навчання наступного місяця для підготовки до іспиту. Наприкінці місяця всі учні складають один і той же тест.

Результати тестування студентів наведено нижче:

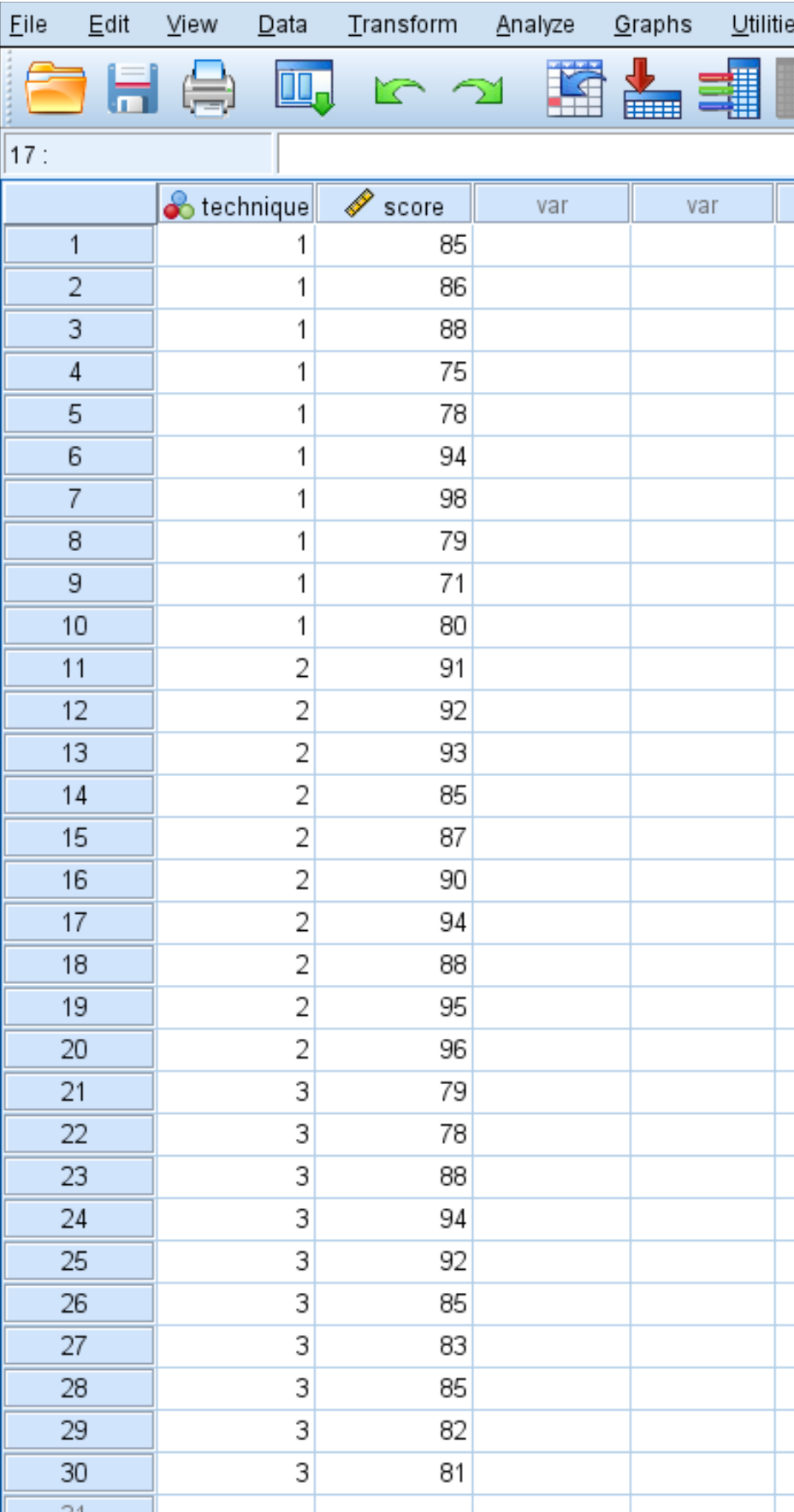
Виконайте наступні дії, щоб виконати односторонній дисперсійний аналіз, щоб визначити, чи однакові середні бали в трьох групах.

Крок 1: Візуалізуйте дані.

По-перше, ми створимо коробкові діаграми для візуалізації розподілу тестових балів для кожного з трьох методів дослідження. Натисніть вкладку «Діаграми» , а потім клацніть «Конструктор діаграм» .

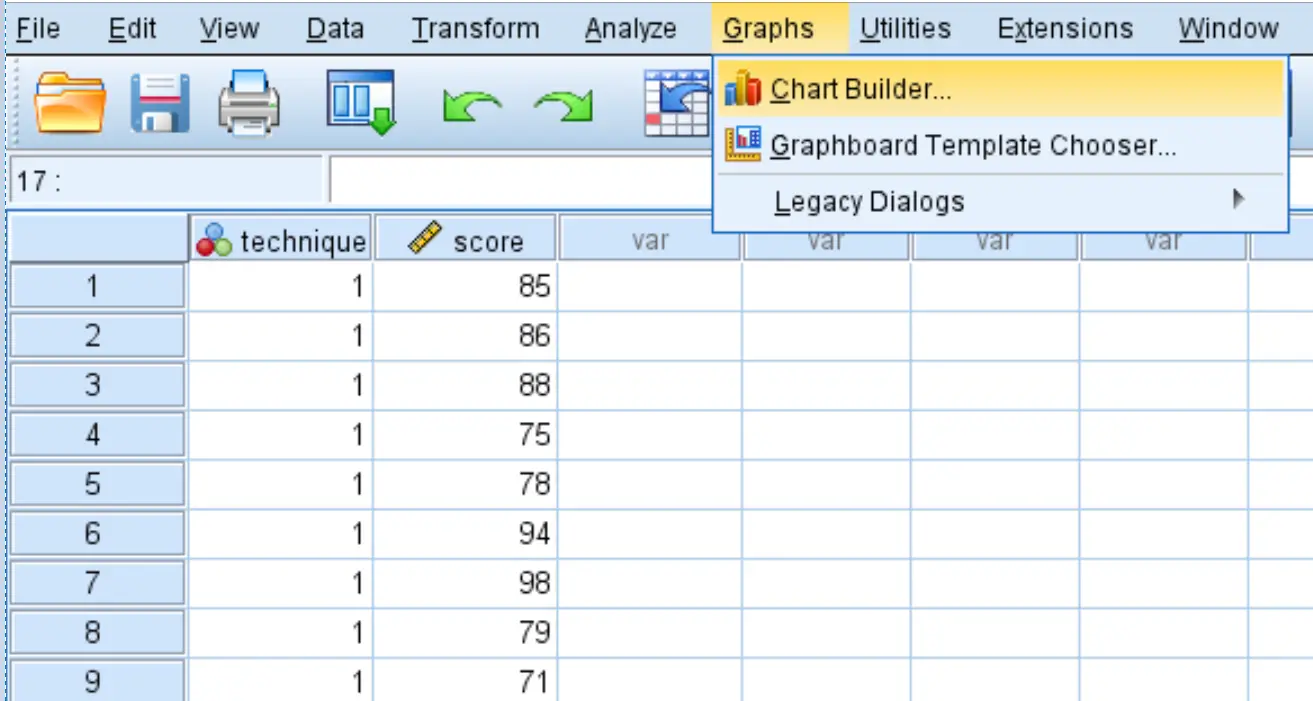
Виберіть Boxplot у вікні Choose from:. Потім перетягніть першу діаграму з позначкою Simple boxplot у головне вікно редагування. Перетягніть технічну змінну на вісь X, а оцінку на вісь Y.

Потім клацніть «Властивості елемента» , потім клацніть «Вісь Y1» . Змініть мінімальне значення на 60. Потім натисніть OK .

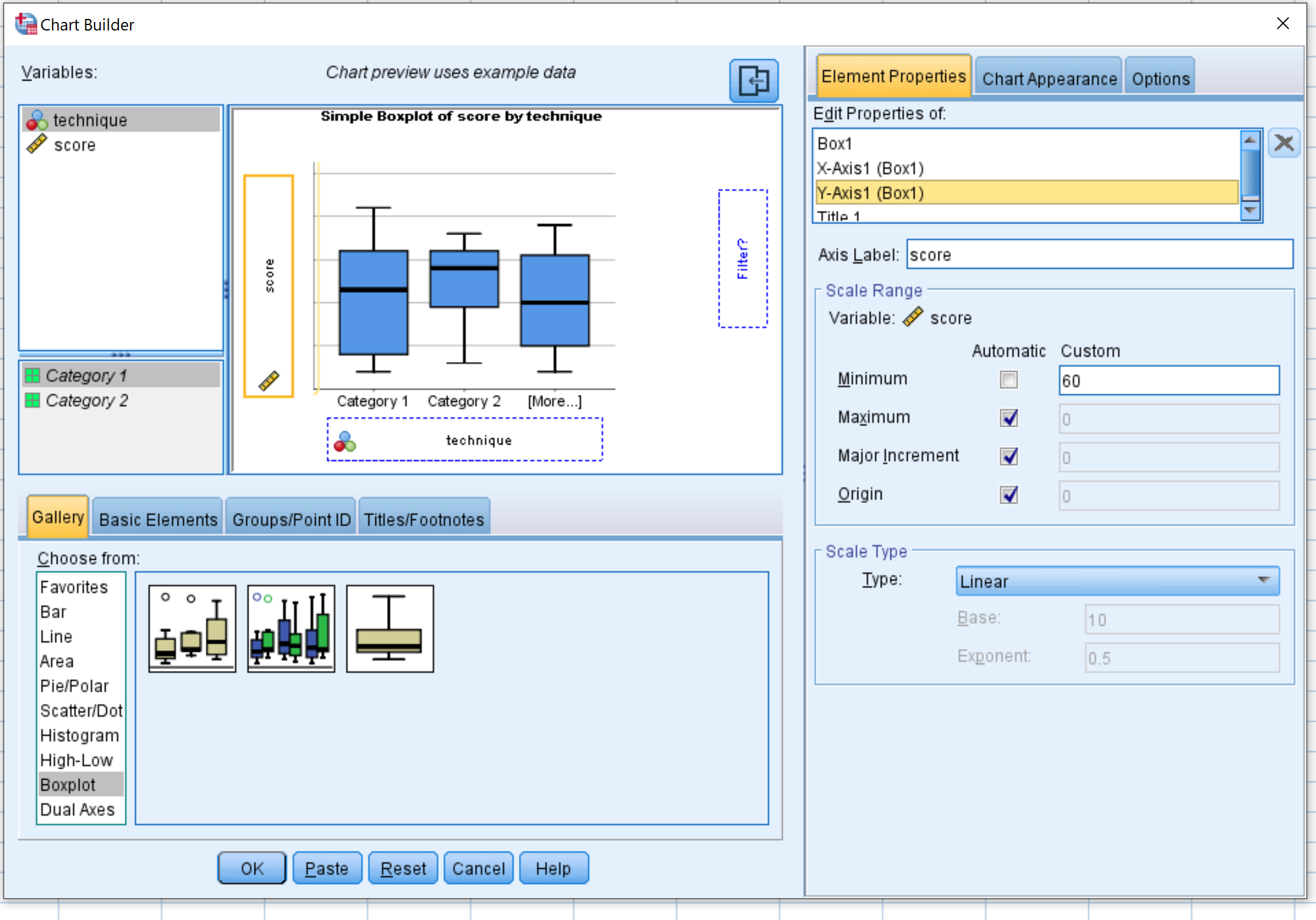
З’являться такі коробкові діаграми:

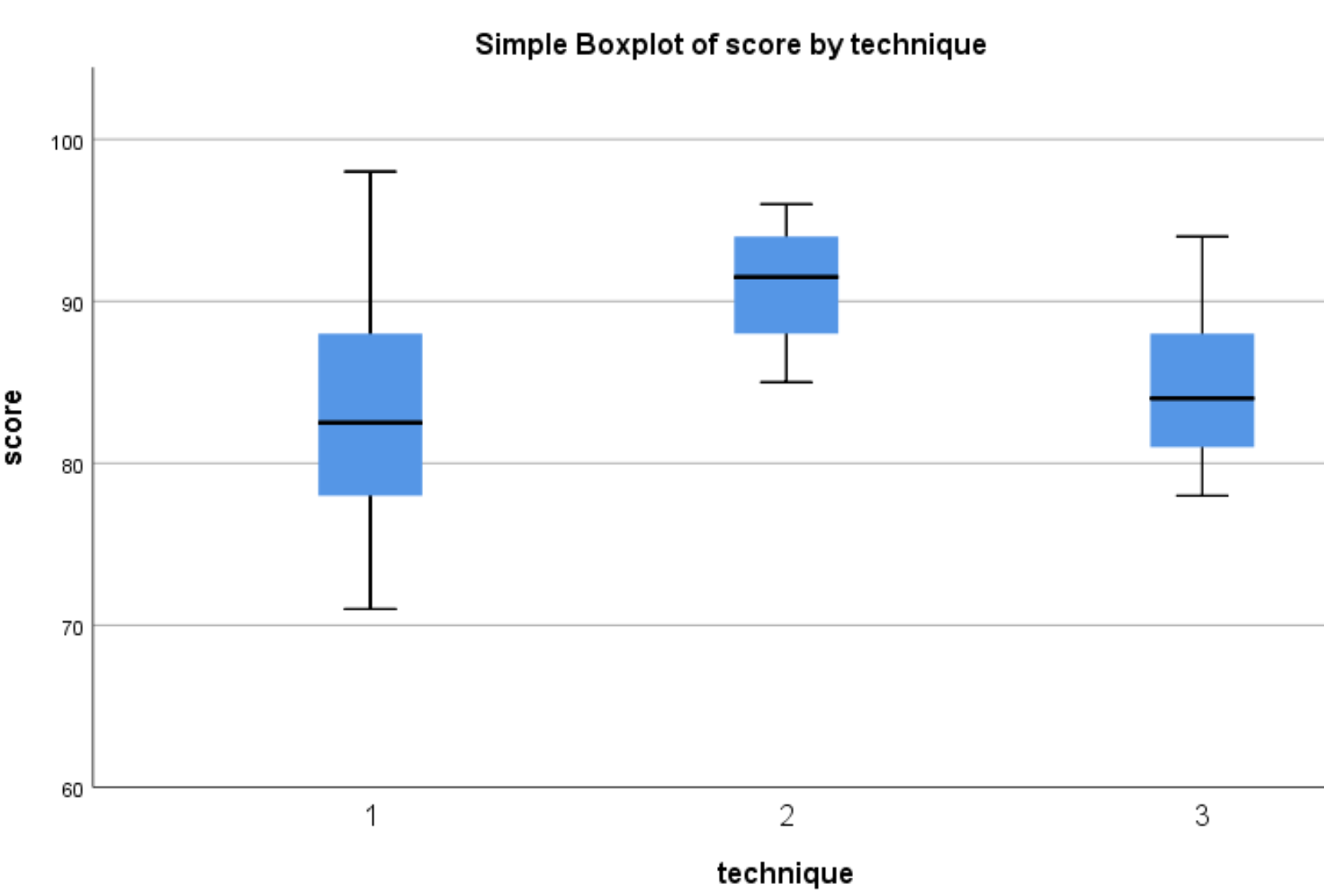
Ми бачимо, що розподіл тестових балів має тенденцію бути вищим для студентів, які використовували Техніку 2, ніж для студентів, які використовували Методи 1 і 3. Щоб визначити, чи є ці відмінності в балах статистично значущими, ми виконаємо односторонній дисперсійний аналіз.

Крок 2: Виконайте односторонній дисперсійний аналіз.

Клацніть вкладку «Аналіз» , потім «Порівняти середні» , потім «Односторонній дисперсійний аналіз» .

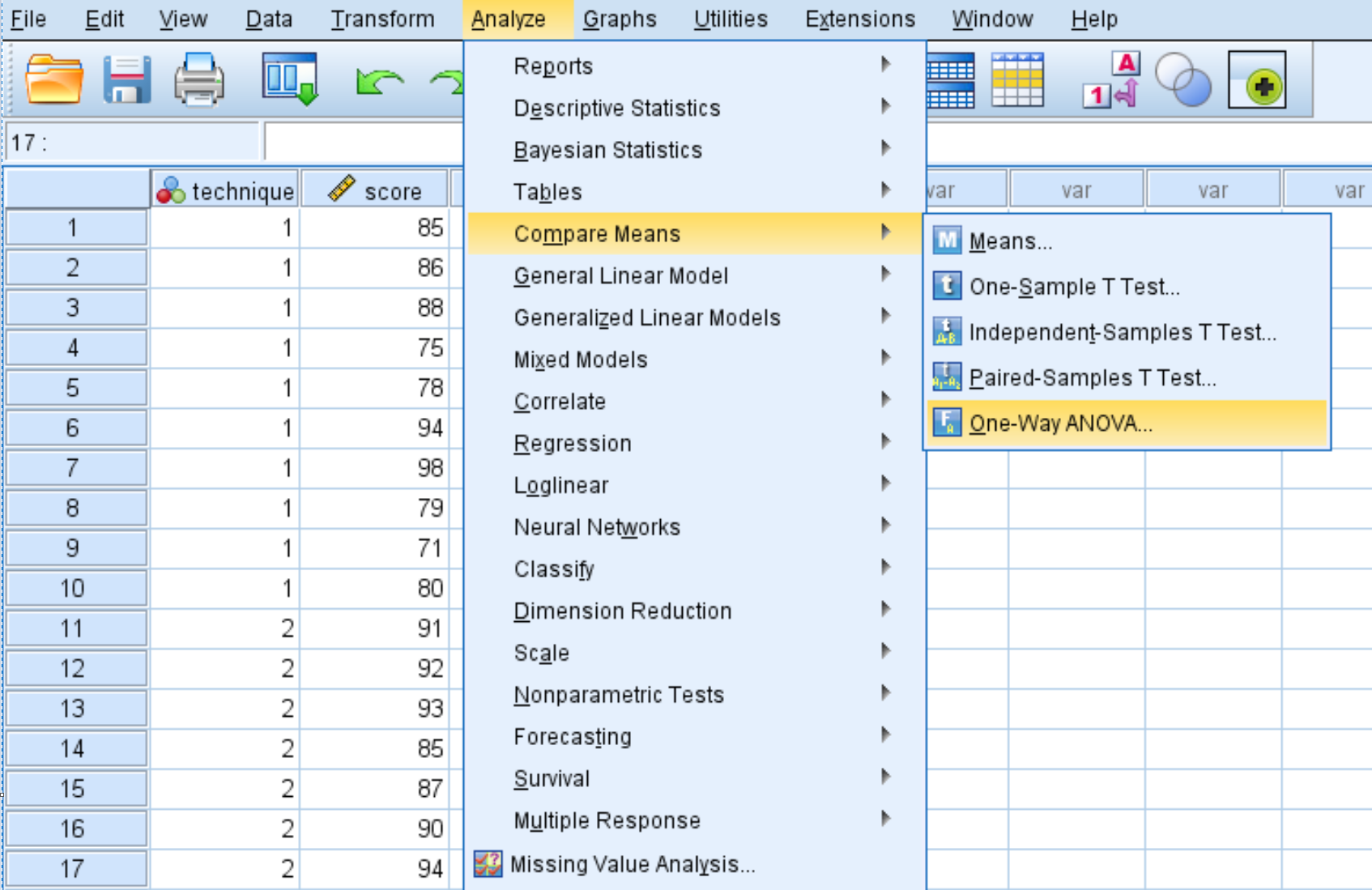
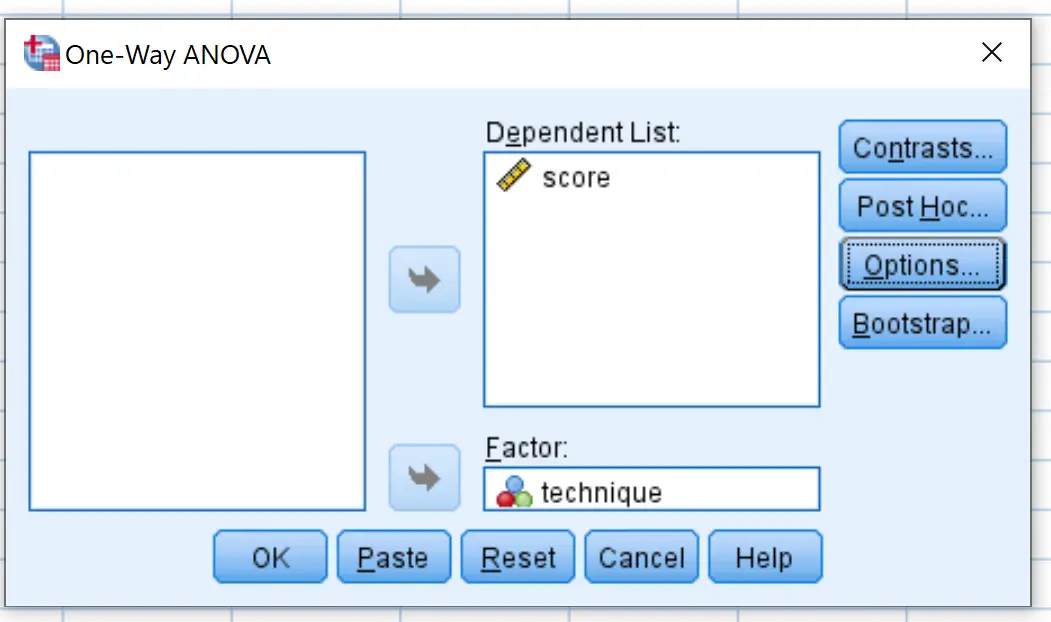
У новому вікні, що з’явиться, помістіть оцінку змінної в поле «Список залежних», а техніку змінної — у поле «Фактор».

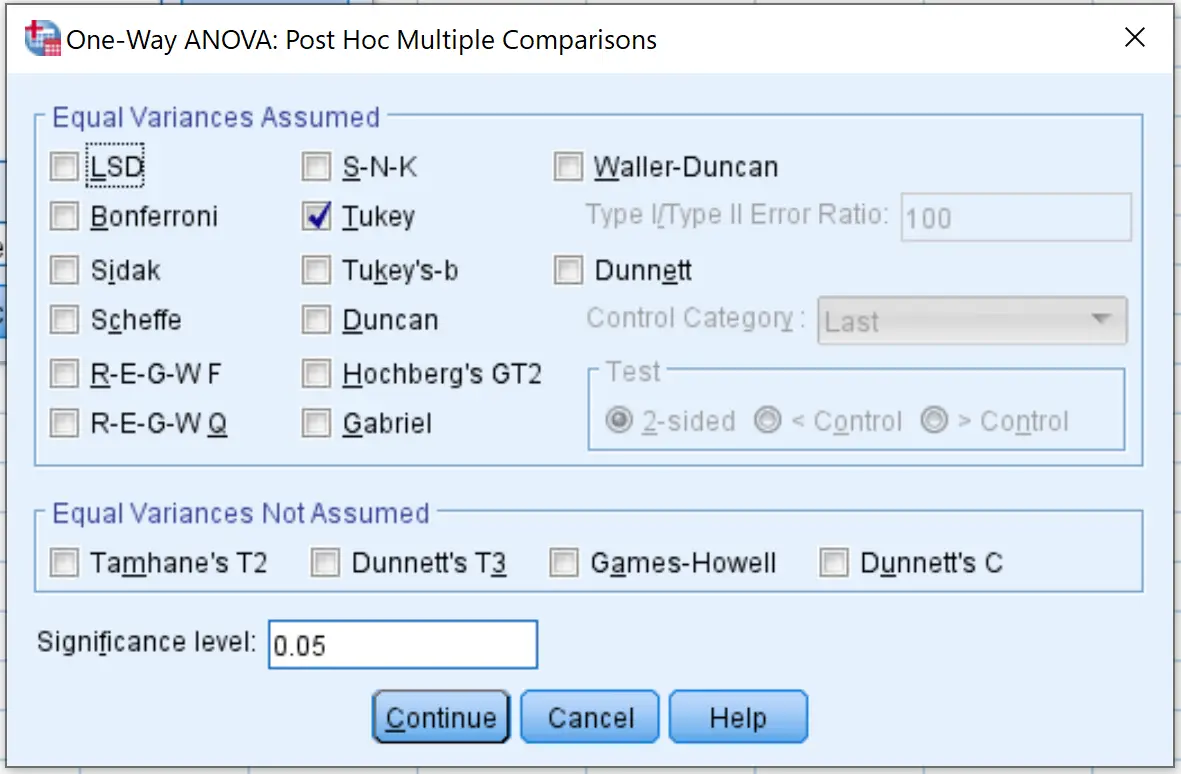
Потім клацніть Post Hoc і поставте прапорець поруч із Tukey . Потім натисніть Продовжити .

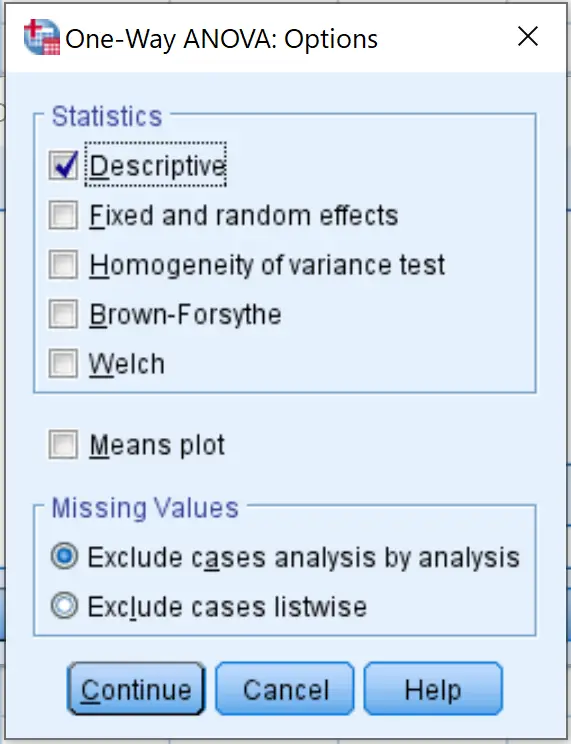
Потім натисніть «Параметри» та встановіть прапорець «Описовий» . Потім натисніть Продовжити .

Нарешті натисніть OK .

Крок 3: Інтерпретація результату.

Після натискання кнопки OK з’являться результати одностороннього дисперсійного аналізу. Ось як інтерпретувати результат:

Опис таблиці

Ця таблиця відображає описову статистику для кожної з трьох груп у нашому наборі даних.

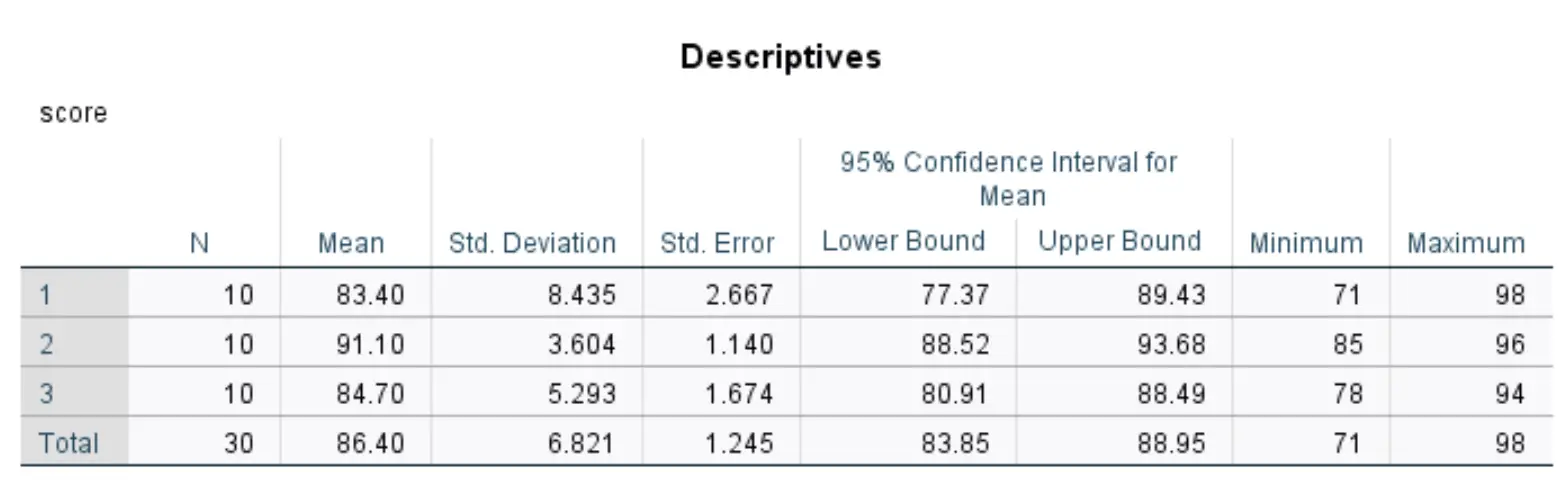
Найбільш актуальні цифри включають:

• N: кількість студентів у кожній групі.
• Середній: середній тестовий бал для кожної групи.
• Стандартний. Відхилення: стандартне відхилення результатів тесту для кожної групи.

Таблиця ANOVA

Ця таблиця відображає результати одностороннього дисперсійного аналізу:

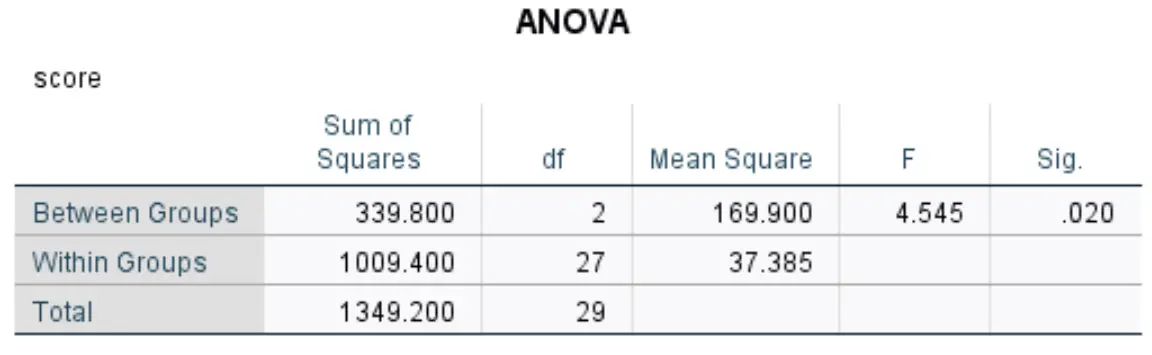
Найбільш актуальні цифри включають:

• F: загальна статистика F.
• Sig: P-значення, яке відповідає статистиці F (4,545) з чисельником df (2) і знаменником df (27). У цьому випадку р-значення виявляється рівним 0,020 .

Нагадаємо, що односторонній дисперсійний аналіз використовує такі нульові та альтернативні гіпотези:

• H ₀ (нульова гіпотеза): μ ₁ = μ ₂ = μ ₃ = … = μ _k (усі середні сукупності рівні)
• H _A (альтернативна гіпотеза): принаймні одне середнє значення сукупності відрізняється   відпочинок

Оскільки p-значення таблиці ANOVA менше 0,05, у нас є достатньо доказів, щоб відхилити нульову гіпотезу та зробити висновок, що принаймні одне з групових середніх відрізняється від інших.

Щоб точно знати, які групові середні відрізняються одне від одного, ми можемо звернутися до останньої таблиці результату ANOVA.

Таблиця множинного порівняння

У цій таблиці показано множинні порівняння Тьюкі між кожною з трьох груп. В основному нас цікавить Sig. стовпець, який відображає р-значення для відмінностей у середніх значеннях між кожною групою:

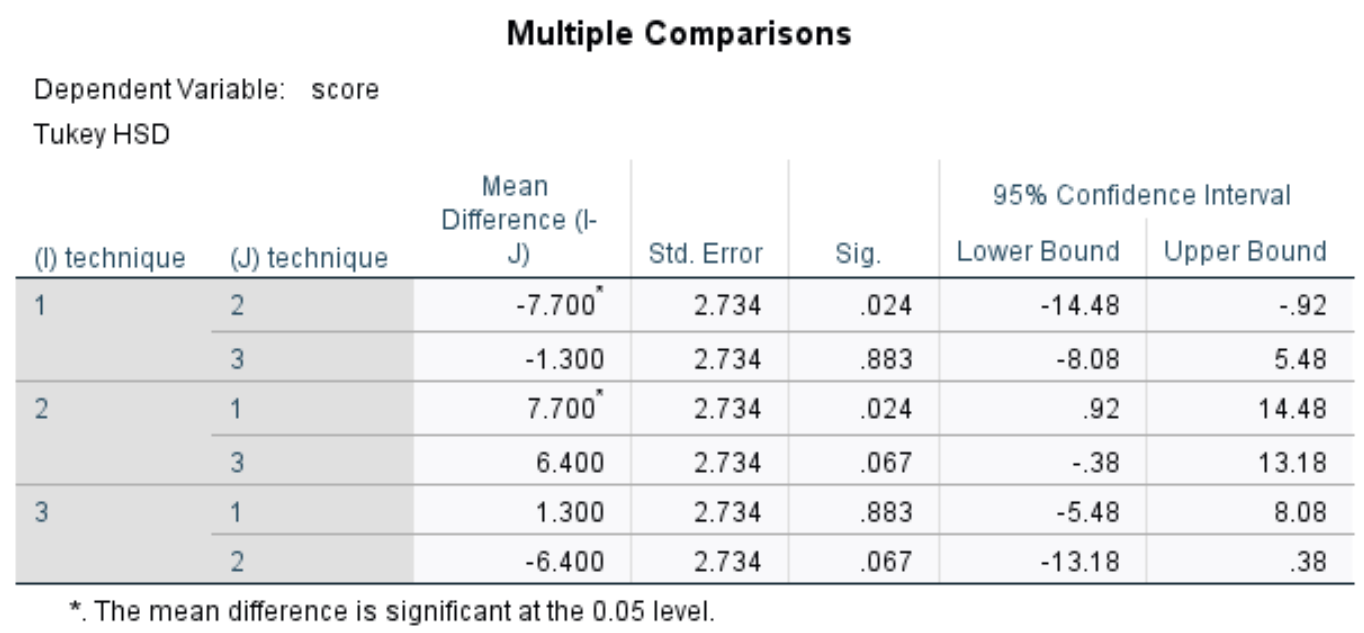
У таблиці ми можемо побачити p-значення для наступних порівнянь:

• Техніка 1 проти 2: | р-значення = 0,024
• Техніка 1 проти 3 | р-значення = 0,883
• Техніка 2 проти 3 | р-значення = 0,067

Єдине групове порівняння з p-значенням менше 0,05 відбувається між Технікою 1 і Технікою 2.

Це говорить нам про те, що існує статистично значуща різниця в середніх результатах тестів між студентами, які використовували Техніку 1, і тими, хто використовував Техніку 2.

Однак немає статистично значущої різниці між методами 1 і 3, а також між методами 2 і 3.

Крок 4: Повідомте про результати.

Нарешті, ми можемо повідомити про результати одностороннього дисперсійного аналізу. Ось приклад того, як це зробити:

Було проведено односторонній дисперсійний аналіз, щоб визначити, чи призвели три різні методи дослідження до різних результатів тесту.

Загалом 10 студентів використовували кожну з трьох методик навчання протягом місяця перед тим, як усі проходили той самий тест.

Односторонній дисперсійний аналіз виявив, що існує статистично значуща різниця в результатах тестів принаймні між двома групами (F(2, 27) = 4,545, p = 0,020).

Тест Тьюкі для множинних порівнянь показав, що середні результати тесту значно відрізнялися між студентами, які використовували Техніку 1 і Техніку 2 (p = 0,024, 95% ДІ = [-14,48, -0,92]).

Не було статистично значущої різниці між оцінками для методик 1 і 3 (p = 0,883) або між оцінками для методик 2 і 3 (p = 0,067).