Що таке однофакторний аналіз? (визначення & #038; приклад)

Термін однофакторний аналіз відноситься до аналізу однієї змінної. Ви можете запам’ятати це, оскільки префікс «uni» означає «один».

Метою однофакторного аналізу є розуміння розподілу значень однієї змінної. Ви можете порівняти цей тип аналізу з наступним:

• Двофакторний аналіз : аналіз двох змінних.
• Багатофакторний аналіз: аналіз двох або більше змінних.

Наприклад, припустимо, що ми маємо такий набір даних:

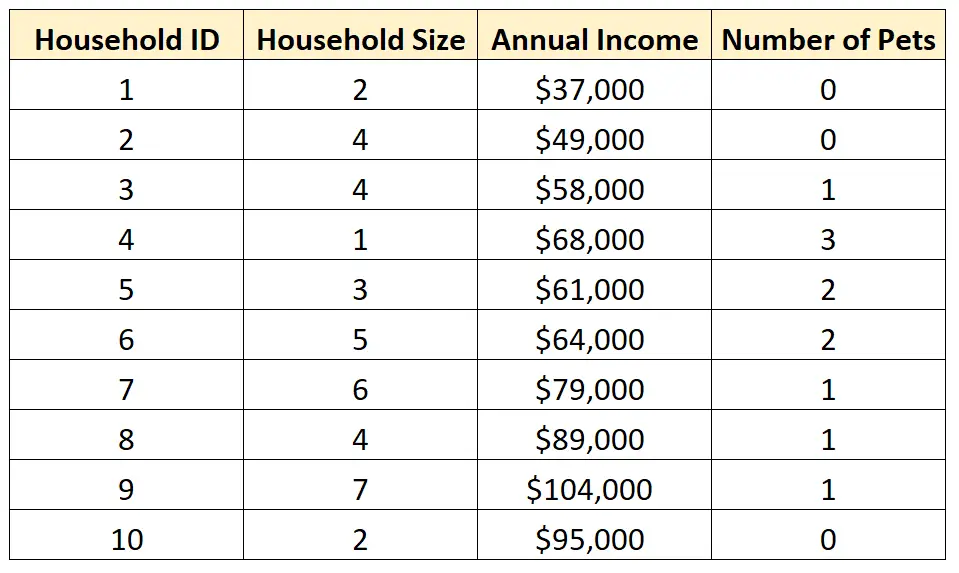
Ми можемо вибрати однофакторний аналіз однієї з окремих змінних у наборі даних, щоб краще зрозуміти розподіл значень.

Наприклад, ми можемо вибрати виконання однофакторного аналізу змінної Розмір домогосподарства :

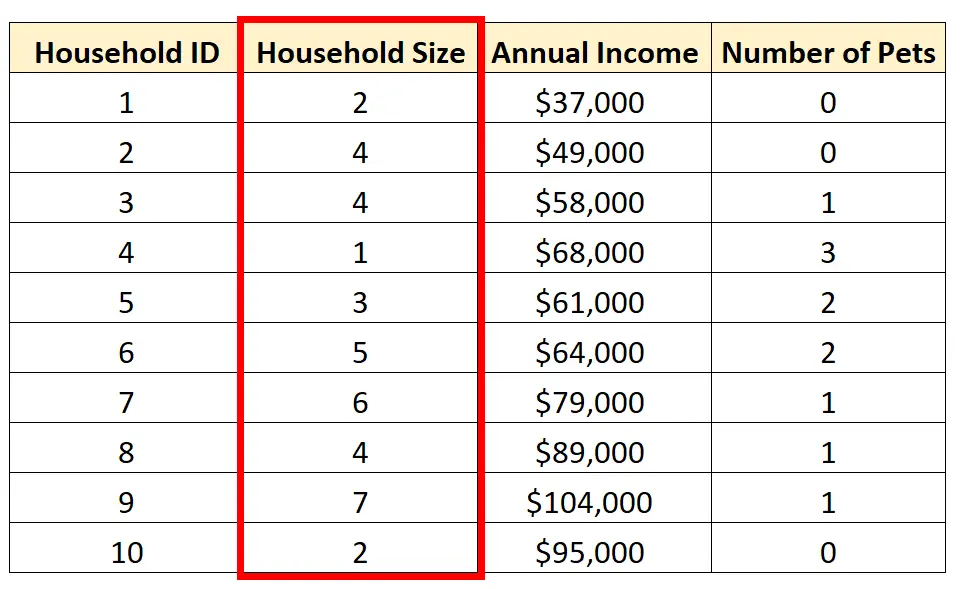
Є три поширені способи виконання однофакторного аналізу:

1. Зведена статистика

Найпоширенішим способом виконання однофакторного аналізу є опис змінної за допомогою підсумкової статистики .

Існує два поширених типи зведеної статистики:

• Показники центральної тенденції : ці числа описують, де знаходиться центр набору даних. Приклади включають середнє значення та медіану .
• Міри дисперсії : ці числа описують розподіл значень у наборі даних. Приклади включають інтервал , інтерквартильний діапазон , стандартне відхилення та дисперсію .

2. Частотні розподіли

Інший спосіб виконання однофакторного аналізу – створити частотний розподіл , який описує, як часто різні значення з’являються в наборі даних.

3. Графіка

Інший спосіб виконання однофакторного аналізу – створення графіків для візуалізації розподілу значень для певної змінної.

Загальні приклади:

• Boxplots
• Гістограми
• Криві густини
• камамбер

У наведених нижче прикладах показано, як виконати кожен тип однофакторного аналізу за допомогою змінної «Розмір домогосподарства » з нашого раніше згаданого набору даних:

Зведена статистика

Ми можемо розрахувати наступні показники центральної тенденції розміру домогосподарства:

• Середнє (середнє значення): 3,8
• Медіана (середнє значення): 4

Ці значення дають нам уявлення про те, де знаходиться «центральна» цінність.

Ми також можемо розрахувати такі міри дисперсії:

• Діапазон (різниця між макс. і мін.): 6
• Інтерквартильна шкала (розподіл середніх 50% значень): 2,5
• Стандартне відхилення (середній показник поширення): 1,87

Ці значення дають нам уявлення про розподіл значень цієї змінної.

Розподіл частоти

Ми також можемо створити наступну таблицю розподілу частот, щоб узагальнити, як часто зустрічаються різні значення:

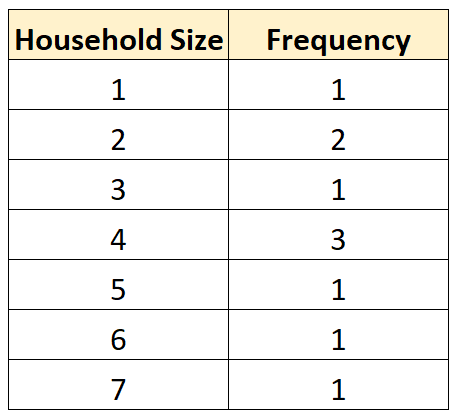
Це дозволяє нам швидко побачити, що найпоширеніший розмір домогосподарства становить 4 особи .

Ресурс: Ви можете використовувати цей калькулятор частоти для автоматичного створення частотного розподілу для будь-якої змінної.

Графіка

Ми можемо створити такі графіки, які допоможуть нам візуалізувати розподіл значень розміру домогосподарства:

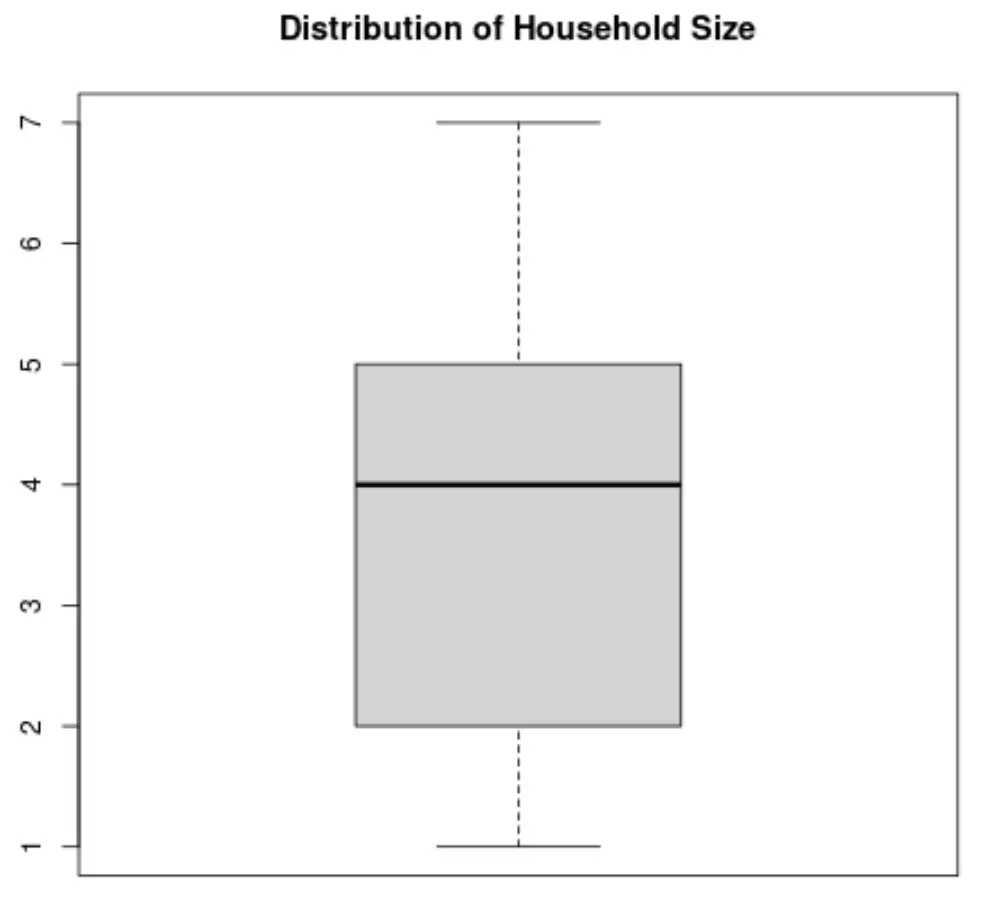
1. Боксплот

Коробковий графік – це графік, який показує п’ятизначний підсумок набору даних.

Зведення з п’яти цифр включає:

• Мінімальне значення
• Перший квартиль
• Середнє значення
• Третій квартиль
• Максимальне значення

Ось як виглядатиме коробкова діаграма для змінної «Розмір домогосподарства»:

Ресурс: Ви можете використовувати цей генератор boxplot для автоматичного створення boxplot для будь-якої змінної.

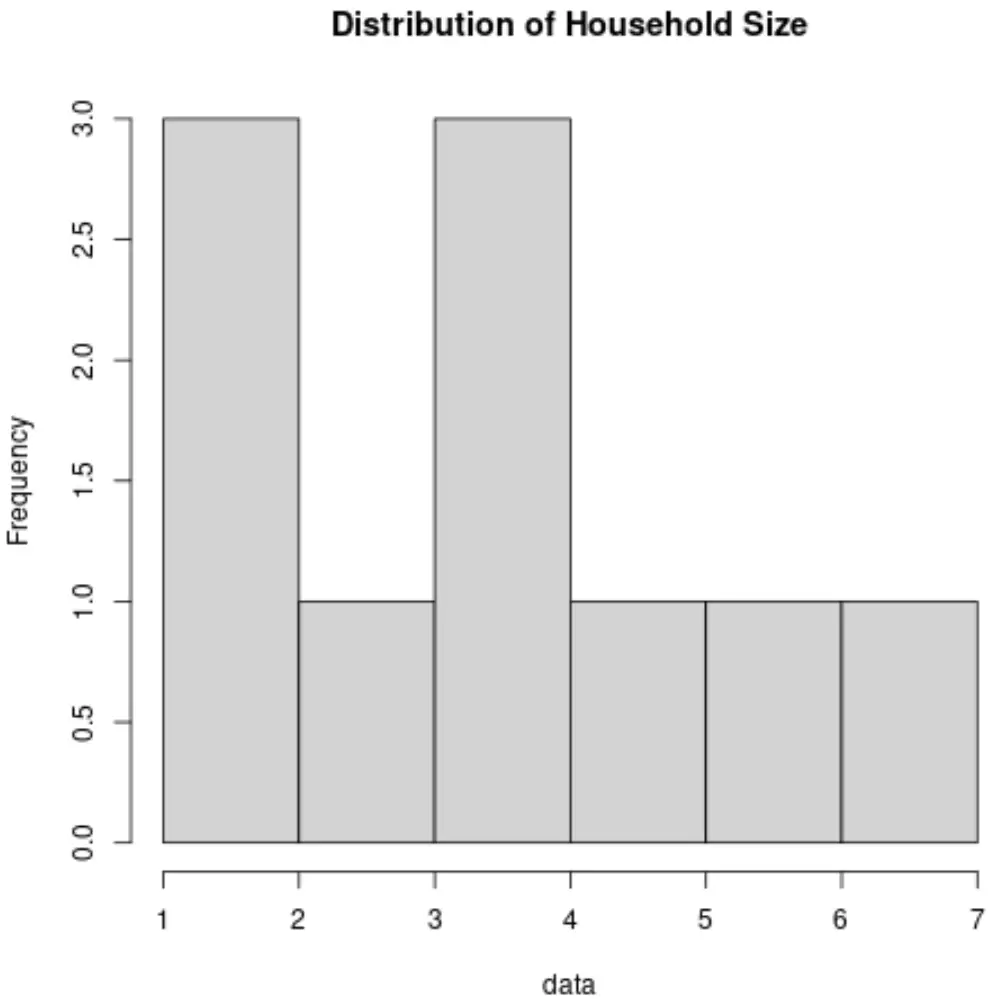
2. Гістограма

Гістограма — це тип діаграми, який використовує вертикальні стовпчики для відображення частот. Цей тип діаграми є корисним способом візуалізації розподілу значень у наборі даних.

Ось як виглядатиме гістограма для змінної «Розмір домогосподарства»:

3. Крива щільності

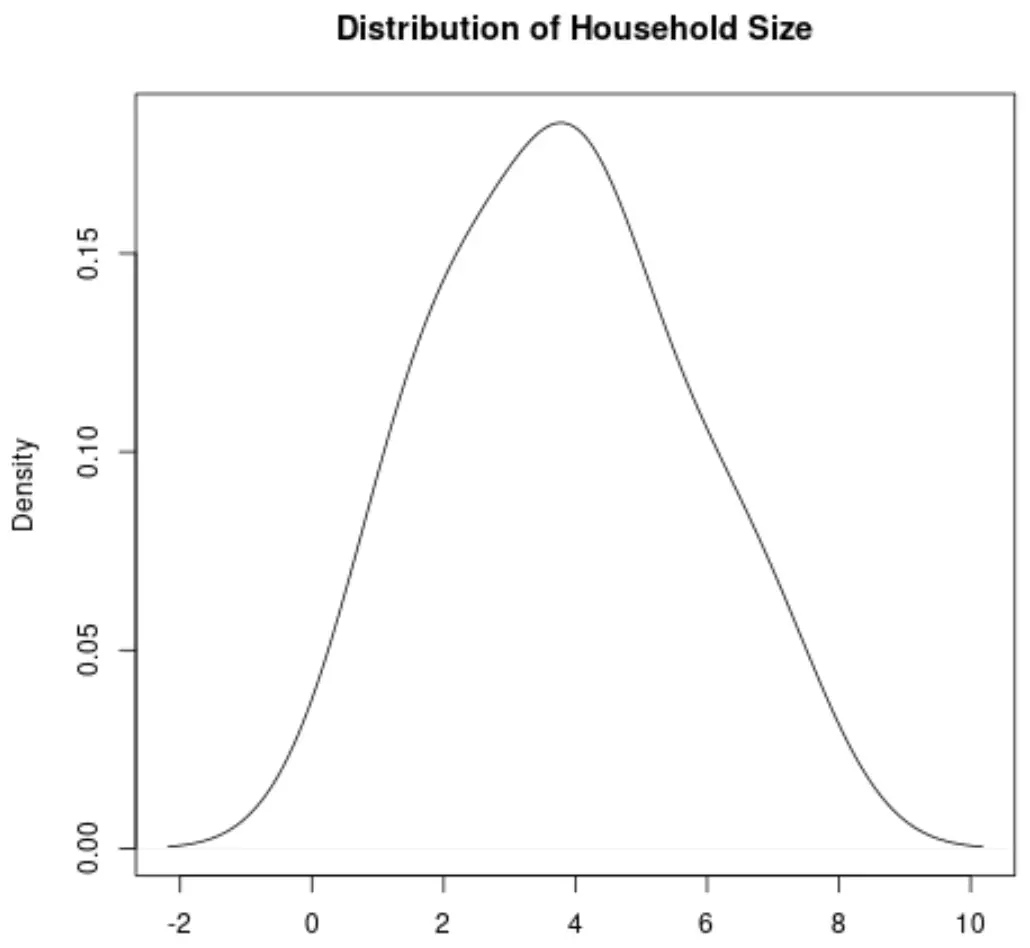
Крива щільності — це крива на графіку, яка представляє розподіл значень у наборі даних.

Це особливо корисно для візуалізації «форми» розподілу, включно з тим, чи має розподіл один або кілька «піків» частих значень і чи є розподіл перекошеним вліво або вправо .

Ось як виглядала б крива щільності для змінної розміру домогосподарства:

4. Кругова діаграма

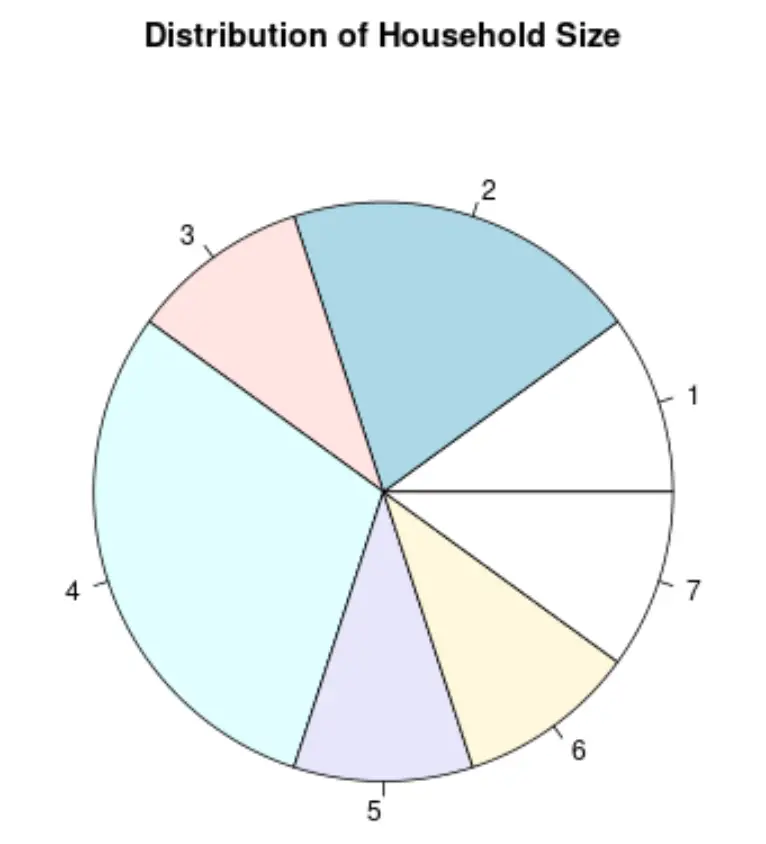
Кругова діаграма — це тип діаграми у формі кола, у якій використовуються зрізи для відображення пропорцій цілого.

Ось як виглядатиме секторна діаграма для змінної «Розмір домогосподарства»:

Залежно від типу даних одна з цих діаграм може бути кориснішою за інші для візуалізації розподілу значень.