Описова чи інференційна статистика: у чому різниця?

Є дві основні галузі в галузі статистики:

• Описова статистика
• Інференційна статистика

Цей посібник пояснює різницю між двома гілками та пояснює, чому кожна з них корисна в певних ситуаціях.

Описова статистика

У двох словах, описова статистика має на меті описати набірнеоброблених даних за допомогою зведеної статистики, графіків і таблиць.

Описова статистика корисна, оскільки вона дозволяє зрозуміти групу даних набагато швидше та легше, ніж просто дивитися на рядки та рядки необроблених значень даних.

Наприклад, скажімо, у нас є набір необроблених даних, що показує результати тестів 1000 учнів певної школи. Нас може зацікавити середній тестовий бал, а також розподіл тестових балів.

Використовуючи описову статистику, ми можемо знайти середній бал і створити графік, який допоможе нам візуалізувати розподіл балів.

Це дозволяє нам набагато легше зрозуміти результати тестів студентів, ніж просто дивитися на необроблені дані.

Загальні форми описової статистики

Існує три поширені форми описової статистики:

1. Зведена статистика. Це статистика, яка підсумовує дані за допомогою одного числа. Існує два поширених типи зведеної статистики:

• Показники центральної тенденції : ці числа описують, де знаходиться центр набору даних. Приклади включають середнє значення   і медіана .
• Міри дисперсії: ці числа описують розподіл значень у наборі даних. Приклади включають інтервал , інтерквартильний діапазон , стандартне відхилення та дисперсію .

2. Графіка . Діаграми допомагають нам візуалізувати дані. Поширені типи діаграм, які використовуються для візуалізації даних, включають коробкові діаграми , гістограми , діаграми стебла та листя та точкові діаграми .

3. Таблиці . Таблиці можуть допомогти нам зрозуміти, як розподіляються дані. Поширеним типом таблиці є частотна таблиця , яка повідомляє нам, скільки значень даних потрапляє в певні діапазони.

Приклад використання описової статистики

Наступний приклад ілюструє, як ми можемо використовувати описову статистику в реальному світі.

Припускається, що 1000 учнів певної школи складають один і той самий тест. Ми хочемо зрозуміти розподіл результатів тестування, тому використовуємо таку описову статистику:

1. Зведена статистика

Середній: 82,13 . Це говорить про те, що середній тестовий бал серед 1000 студентів становить 82,13.

Медіана: 84. Це говорить нам про те, що половина всіх студентів набрала більше 84 балів, а друга половина — нижче 84.

Макс.: 100. Мінім.: 45. Це говорить нам про те, що максимальний бал, отриманий будь-яким учнем, становив 100, а мінімальний — 45. Діапазон — який показує різницю між максимальним і мінімальним — становить 55.

2. Графіка

Щоб візуалізувати розподіл результатів тесту, ми можемо створити гістограму – тип діаграми, яка використовує прямокутні стовпчики для представлення частот.

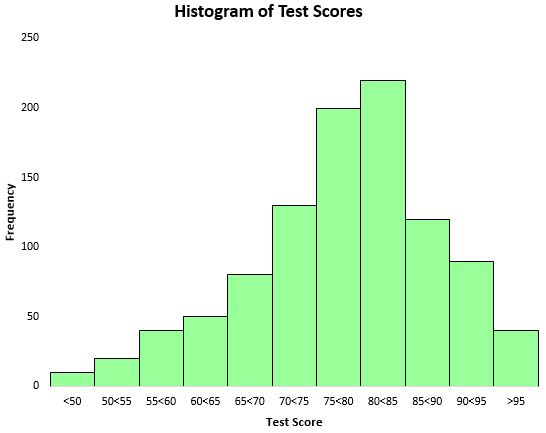
Грунтуючись на цій гістограмі, ми бачимо, що розподіл тестових балів має приблизно дзвоноподібну форму. Більшість студентів набрали від 70 до 90 балів, у той час як дуже небагато отримали бали вище 95 і ще менше балів нижче 50.

3. Таблиці

Ще один простий спосіб зрозуміти розподіл балів — створити частотну таблицю. Наприклад, наведена нижче частотна таблиця показує відсоток студентів, які набрали бали між різними діапазонами:

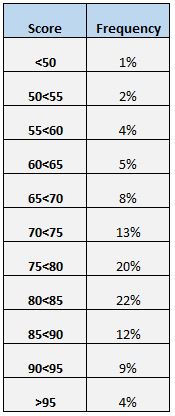
Ми бачимо, що лише 4% від загальної кількості студентів отримали більше 95 балів. Ми також бачимо, що (12% + 9% + 4% = ) 25% усіх студентів отримали 85 або вище.

Таблиця частот особливо корисна, якщо ми хочемо знати, який відсоток значень даних вище або нижче певного значення. Наприклад, припустімо, що школа вважає «прийнятним» результатом тесту будь-який бал вище 75.

Дивлячись на частотну таблицю, ми можемо легко побачити, що (20% + 22% + 12% + 9% + 4% = ) 67% студентів отримали прийнятний бал на тесті.

Інференційна статистика

У двох словах, інференційна статистика використовує невелику вибірку даних, щоб зробити висновки щодо більшої сукупності, з якої зроблено вибірку.

Наприклад, ми можемо захотіти зрозуміти політичні уподобання мільйонів людей у країні.

Однак було б надто довго і дорого обстежити кожну людину в країні. Отже, натомість ми б провели менше опитування, скажімо, 1000 американців, і використали його результати, щоб зробити висновки про населення в цілому.

Це вся передумова інференційної статистики: ми хочемо відповісти на запитання про сукупність, тому ми отримуємо дані для невеликої вибірки цієї сукупності та використовуємо дані вибірки, щоб зробити висновки щодо сукупності.

Важливість репрезентативної вибірки

Для того, щоб бути впевненими в нашій здатності використовувати вибірку, щоб зробити висновки про сукупність, ми повинні переконатися, що у нас є репрезентативна вибірка , тобто вибірка, в якій характеристики індивідуумів у сукупності. Вибірка точно відповідає вибірці характеристики. від загального населення.

В ідеалі ми хочемо, щоб наша вибірка нагадувала «міні-версію» нашої сукупності. Таким чином, якщо ми хочемо зробити висновки щодо сукупності студентів, яка складається з 50% дівчат і 50% хлопчиків, наша вибірка не була б репрезентативною, якби вона включала 90% хлопчиків і лише 10% дівчат.

Якщо наша вибірка не схожа на загальну сукупність, ми не можемо впевнено узагальнити результати вибірки на загальну сукупність.

Як отримати репрезентативну вибірку

Щоб максимізувати шанси отримати репрезентативну вибірку, вам слід зосередитися на двох речах:

1. Переконайтеся, що ви використовуєте метод випадкової вибірки.

Існує кілька методів випадкової вибірки , які, ймовірно, дадуть репрезентативну вибірку, зокрема:

• Проста випадкова вибірка
• Систематична випадкова вибірка
• Кластерна випадкова вибірка
• Стратифікована випадкова вибірка

Методи випадкової вибірки, як правило, створюють репрезентативні вибірки, оскільки кожен член сукупності має рівні шанси потрапити до вибірки.

2. Переконайтеся, що розмір вашої вибірки достатньо великий .

Окрім використання відповідного методу вибірки, важливо переконатися, що вибірка достатньо велика, щоб у вас було достатньо даних для узагальнення на більшу сукупність.

Щоб визначити розмір вибірки, вам потрібно врахувати розмір сукупності, яку ви вивчаєте, рівень достовірності, який ви бажаєте використовувати, і межу похибки, яку ви вважаєте прийнятною.

На щастя, ви можете скористатися онлайн-калькуляторами, щоб ввести ці значення та побачити, яким має бути розмір вашої вибірки.

Поширені форми логічної статистики

Існує три поширені форми інференційної статистики:

1. Перевірка гіпотези.

Ми часто хочемо відповісти на запитання про групу населення, наприклад:

• Чи відсоток людей в Огайо, які підтримують кандидата А, перевищує 50%?
• Чи дорівнює середня висота певної рослини 14 дюймам?
• Чи є різниця між середнім зростом учнів у школах А та Б?

Щоб відповісти на ці запитання, ми можемо виконати перевірку гіпотез , яка дає нам змогу використовувати дані з вибірки, щоб зробити висновки щодо сукупностей.

2. Довірчі інтервали .

Іноді ми хочемо оцінити певне значення для сукупності. Наприклад, нас може зацікавити середня висота певного виду рослин в Австралії.

Замість того, щоб ходити й вимірювати кожну рослину в країні, ми могли б зібрати невелику пробу рослин і виміряти кожну. Тоді ми можемо використовувати середню висоту рослин у вибірці, щоб оцінити середню висоту популяції.

Проте наша вибірка навряд чи дасть ідеальну оцінку населення. На щастя, ми можемо пояснити цю невизначеність, створивши довірчий інтервал , який надає діапазон значень, у межах якого ми впевнені, що знаходиться справжній параметр сукупності.

Наприклад, ми могли б отримати 95% довірчий інтервал [13,2, 14,8], тобто ми на 95% впевнені, що справжня середня висота цього виду рослин становить від 13,2 дюйма до 14,8 дюйма.

3. Регресія .

Іноді ми хочемо зрозуміти зв’язок між двома змінними в популяції.

Наприклад, скажімо, ми хочемо знати, чи години, витрачені на навчання на тиждень, пов’язані з результатами тестів . Щоб відповісти на це запитання, ми могли б виконати техніку, відому як регресійний аналіз .

Отже, ми можемо переглянути кількість вивчених годин, а також результати тестів для 100 студентів і виконати регресійний аналіз, щоб побачити, чи існує значний зв’язок між двома змінними.

Якщо p-значення регресії виявляється значущим , то можна зробити висновок, що існує значний зв’язок між цими двома змінними в загальній популяції студентів.

Різниця між описовою та інференційною статистикою

Підсумовуючи, різницю між описовою та інференціальною статистикою можна описати так:

Описова статистика використовує зведену статистику, графіки та таблиці для опису набору даних.

Це корисно, оскільки допомагає нам швидко та легко зрозуміти набір даних, не переглядаючи всі окремі значення даних.

Інференційна статистика використовує вибірки, щоб зробити висновки про більшу сукупність.

Залежно від питання про генеральну сукупність, на яке ви хочете відповісти, ви можете вирішити використати один або кілька з таких методів: перевірка гіпотез, довірчі інтервали та регресійний аналіз.

Якщо ви вирішите використовувати один із цих методів, майте на увазі, що ваша вибірка має бути репрезентативною для вашої сукупності , інакше висновки, які ви зробите, не будуть надійними.