Перевірка гіпотези для середнього

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке перевірка гіпотез для середнього значення в статистиці. Таким чином, ви знайдете формулу перевірки гіпотези для середнього значення та, крім того, крок за кроком розв’язану вправу.

Що таке перевірка гіпотези для середнього?

Перевірка гіпотези для середнього — це статистичний метод, який використовується для відхилення або відхилення нульової гіпотези середнього значення сукупності.

Якщо говорити точніше, перевірка гіпотези для середнього включає обчислення тестової статистики та порівняння її з критичним значенням, щоб відхилити нульову гіпотезу чи ні.

Слід зазначити, що перевірки гіпотез мають різні назви; у статистиці вони також називаються контрастами гіпотез, перевірками гіпотез або перевірками значущості.

Формула перевірки гіпотези для середнього

Далі ми побачимо, як обчислюється статистика перевірки гіпотези для середнього. Однак формула дещо змінюється залежно від того, відома дисперсія чи ні, тому ми спочатку побачимо, як це робиться, коли дисперсія відома, а потім, коли дисперсія невідома.

З відомим відхиленням

Формула перевірки гіпотези для середнього з відомою дисперсією :

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle \frac{\sigma}{\sqrt{n}}}$

золото:

$Z$

це статистика перевірки гіпотези для середнього.
$\overline{x}$

це зразок засобів.
$\mu$

є запропонованим середнім значенням.
$\sigma$

стандартне відхилення сукупності.
$n$

це розмір вибірки.

Після того, як статистику перевірки гіпотези для середнього розраховано, результат слід інтерпретувати як відхилення або відхилення нульової гіпотези:

Якщо перевірка гіпотези для середнього є двосторонньою, нульова гіпотеза відхиляється, якщо абсолютне значення статистики перевищує критичне значення Z _α/2 .
Якщо перевірка гіпотези для середнього збігається з правим хвостом, нульова гіпотеза відхиляється, якщо статистичне значення перевищує критичне значення Z _α .
Якщо перевірка гіпотези для середнього збігається з лівим хвостом, нульова гіпотеза відхиляється, якщо статистичне значення менше критичного значення -Z _α .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

У цьому випадку критичні значення отримують із стандартизованої таблиці нормального розподілу .

З невідомою дисперсією

Формула перевірки гіпотези для середнього з невідомою дисперсією :

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

золото:

$t$

є статистикою перевірки гіпотези для середнього значення, яке визначається t-розподілом Стьюдента .
$\overline{x}$

це зразок засобів.
$\mu$

є запропонованим середнім значенням.
$s$

є стандартним відхиленням вибірки.
$n$

це розмір вибірки.

Як і раніше, розрахований результат тестової статистики має бути інтерпретований з критичним значенням, щоб відхилити чи ні нульову гіпотезу:

Якщо перевірка гіпотези для середнього є двосторонньою, нульова гіпотеза відхиляється, якщо абсолютне значення статистики перевищує критичне значення t _α/2|n-1 .
Якщо перевірка гіпотези для середнього збігається з правим хвостом, нульова гіпотеза відхиляється, якщо статистичне значення перевищує критичне значення t _α|n-1 .
Якщо перевірка гіпотези для середнього збігається з лівим хвостом, нульова гіпотеза відхиляється, якщо статистика менша за критичне значення -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Коли дисперсія невідома, критичні тестові значення отримують з таблиці розподілу Стьюдента.

Реальний приклад перевірки гіпотези для середнього значення

Щоб повністю зрозуміти концепцію перевірки гіпотези для середньої генеральної сукупності, ви можете побачити реальний приклад такого типу перевірки гіпотези нижче.

Технологічна компанія стверджує, що батарея ноутбука, який вона продає, працює 6 годин. Ми перевіряємо, чи ця гіпотеза хибна, виконуючи перевірку гіпотези з рівнем значущості α = 0,05. Для цього вирішено придбати 20 одиниць і спостерігати за часом автономної роботи кожного комп’ютера (значення виражені в годинах):

5,2 5,9 7,1 4,2 6,5
8,5 4,6 6,8 6,9 5,8
5,1 6,5 7,0 5,3 6,2
5,7 6,6 7,5 5,1 6,1

У цьому випадку нульова та альтернативна гіпотези перевірки гіпотези про середнє значення такі:

$\begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}$

Щоб визначити статистику тесту, нам спочатку потрібно обчислити середнє значення вибірки та стандартне відхилення вибірки:

$\overline{x}=6,13 \qquad s=1,05$

Оскільки ми не знаємо дисперсію сукупності, щоб отримати тестову статистику, нам потрібно застосувати формулу перевірки гіпотези для середнього з невідомою дисперсією:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

$\displaystyle t=\frac{6,13-6}{\displaystyle \frac{1,05}{\sqrt{20}}}$

$\displaystyle t=0,68$

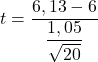
Тепер нам потрібно знайти критичне значення перевірки гіпотези, тому ми шукаємо відповідне значення в таблиці розподілу t Стьюдента . Ступені свободи t Стьюдента на одиницю менші, ніж розмір вибірки (20-1=19), і, з іншого боку, відповідна ймовірність становить половину рівня значущості (0,05/2= 0,025), оскільки це двосторонній перевірка гіпотези.

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}$

На завершення, оскільки це двостороння перевірка гіпотези, а абсолютне значення тестової статистики менше критичного значення, нульова гіпотеза не відхиляється, але альтернативна гіпотеза відхиляється.

$0,68<2,093 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

Перевірка гіпотези на різницю в середніх

Перевірка гіпотези різниці середніх значень використовується для відхилення або прийняття нульової гіпотези про те, що середні значення двох популяцій однакові.

Таким чином, нульова гіпотеза перевірки гіпотези різниці двох середніх завжди така:

$H_0: \mu_1=\mu_2$

Тоді як альтернативною гіпотезою може бути одна з наступних трьох:

$\begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}$

Тоді формула для розрахунку статистики перевірки гіпотези для різниці середніх значень, коли дисперсія відома, виглядає так:

$\displaystyle Z=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

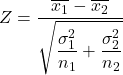
золото:

$Z$

це статистика перевірки гіпотези для різниці двох середніх значень з відомою дисперсією, яка відповідає стандартному нормальному розподілу.
$\overline{x_1}$

є середнім значенням зразка 1.
$\overline{x_2}$

є середнім значенням зразка 2.
$\sigma_1^2$

є дисперсією сукупності 1.
$\sigma_2^2$

це дисперсія сукупності 2.
$n_1$

розмір вибірки 1.
$n_2$

розмір вибірки 2.

З іншого боку, формула для розрахунку статистики перевірки гіпотези для різниці середніх значень, коли дисперсія невідома, виглядає наступним чином:

$\displaystyle t=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

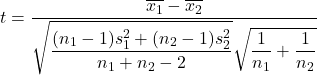
золото:

$t$

це статистика перевірки гіпотези для різниці двох середніх значень із невідомою дисперсією, яка відповідає t-розподілу Стьюдента.
$\overline{x_1}$

є середнім значенням зразка 1.
$\overline{x_2}$

є середнім значенням зразка 2.
$s_1^2$

є дисперсією зразка 1.
$s_2^2$

є дисперсією зразка 2.
$n_1$

розмір вибірки 1.
$n_2$

розмір вибірки 2.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке перевірка гіпотези для середнього?

Формула перевірки гіпотези для середнього

З відомим відхиленням

З невідомою дисперсією

Реальний приклад перевірки гіпотези для середнього значення

Перевірка гіпотези на різницю в середніх

Про автора

Редакція

Додати коментар