Перевірка гіпотези на дисперсію

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке перевірка гіпотез на дисперсію. Отже, ви знайдете формулу для перевірки дисперсійної гіпотези та, крім того, крок за кроком розв’язану вправу.

Що таке перевірка гіпотези на дисперсію?

Перевірка гіпотези на дисперсію – це статистичний метод, який використовується для визначення того, чи варто відхиляти нульову гіпотезу про дисперсію сукупності. Іншими словами, перевірка дисперсійної гіпотези використовується для відхилення або прийняття гіпотези про значення дисперсії сукупності.

Зокрема, залежно від значення статистики перевірки гіпотези для дисперсії та вибраного рівня значущості нульова гіпотеза відхиляється або приймається.

Майте на увазі, що перевірка гіпотез має багато назв, її також можна назвати протиставленням гіпотез, перевіркою гіпотез або перевіркою значущості.

Формула перевірки гіпотези для дисперсії

Статистика перевірки гіпотези для дисперсії дорівнює різниці між розміром вибірки, помноженою на одиницю дисперсії вибірки, і поділеною на запропоноване значення дисперсії сукупності. Статистика перевірки гіпотези для дисперсії має розподіл хі-квадрат .

Таким чином, формула для розрахунку статистики перевірки гіпотези для дисперсії виглядає наступним чином:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

золото:

$\chi^2$

це статистика перевірки гіпотези для дисперсії, яка має розподіл хі-квадрат.
$n$

це розмір вибірки.
$s^2$

дисперсія вибірки.
$\sigma^2$

є запропонованою дисперсією сукупності.

Щоб інтерпретувати результат статистики, отримане значення необхідно порівняти з критичним значенням тесту.

Якщо перевірка гіпотези на дисперсію є двосторонньою, нульова гіпотеза відхиляється, якщо статистичне значення перевищує критичне значення.
$\chi_{1-\alpha/2|n-1}^2$

або якщо критичне значення менше

$\chi_{\alpha/2|n-1}$

.
Якщо перевірка гіпотези на дисперсію збігається з правим хвостом, нульова гіпотеза відхиляється, якщо статистика перевищує критичне значення
$\chi_{1-\alpha|n-1}^2$

.
Якщо перевірка гіпотези на дисперсію збігається з лівим хвостом, нульова гіпотеза відхиляється, якщо статистика менша за критичне значення
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

Критичні значення перевірки гіпотези для дисперсії отримують з таблиці розподілу хі-квадрат. Зверніть увагу, що ступені свободи для розподілу хі-квадрат є розміром вибірки мінус 1.

Реальний приклад перевірки гіпотези на дисперсію

Ознайомившись з визначенням дисперсійної перевірки гіпотези та її формулою, ми побачимо конкретний приклад, щоб завершити засвоєння цієї концепції.

На заводі є машина, яка виготовляє деталі для автомобіля з високою точністю. Однак є підозри, що він відійшов і тепер виробляє деталі із зазором понад 8 мм ² . Щоб спростувати цю гіпотезу, аналізується зразок із 25 штук, дисперсія якого становить 9,1 мм ² . Чи можна відхилити вихідну гіпотезу з рівнем значущості α=0,05?

Нульова гіпотеза та альтернативна гіпотеза для цього тесту гіпотези дисперсії такі:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”> Щоб визначити, чи можна відхилити нульову гіпотезу, ми обчислюємо статистику перевірки гіпотези для дисперсії за допомогою формули, яку ми бачили вище: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

Тепер шукаємо критичне значення, що відповідає правому хвістові для 24 ступенів свободи та рівня значущості α=0,05 у таблиці розподілу Хі-квадрат:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

Таким чином, розрахована статистика є меншою за критичне значення тесту, і тому нульова гіпотеза перевірки гіпотези дисперсії не відхиляється, а скоріше відхиляється альтернативна гіпотеза.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ Див.: Перевірка гіпотези для середнього значення сукупності
➤ Див.: Перевірка гіпотез щодо частки населення

Перевірка гіпотези щодо дисперсії двох сукупностей

Перевірка дисперсійної гіпотези двох популяцій використовується для відхилення або прийняття гіпотези про те, що дисперсії двох різних сукупностей рівні.

Таким чином, нульова гіпотеза перевірки гіпотези щодо дисперсії двох сукупностей завжди така:

$H_0: \sigma^2_1=\sigma^2_2$

А альтернативною гіпотезою може бути один із трьох варіантів:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

У цьому випадку формула для розрахунку статистики перевірки гіпотези для дисперсії двох сукупностей має вигляд:

$F=\cfrac{s_1^2}{s_2^2}$

золото:

$F$

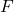
це статистика перевірки гіпотези для дисперсії двох генеральних сукупностей, яка відповідає F-розподілу .
$\sigma_1^2$

є дисперсією сукупності 1.
$\sigma_2^2$

це дисперсія сукупності 2.
$s_1^2$

є дисперсією зразка 1.
$s_2^2$

є дисперсією зразка 2.
$n_1$

розмір вибірки 1.
$n_2$

розмір вибірки 2.

Оскільки F-розподіл Снедекора не є симетричним, нульову гіпотезу відхиляють на основі таких критеріїв:

[latex]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{чорний} \ \text{Якщо }F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше