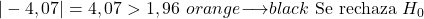Перевірка гіпотези пропорції

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється частка перевірки гіпотез у статистиці. Таким чином, ви знайдете формулу для перевірки гіпотези пропорції та, крім того, покрокову вправу, щоб повністю зрозуміти, як це робиться.

Що таке перевірка гіпотези щодо пропорції?

Перевірка гіпотези пропорції — це статистичний метод, який використовується для визначення того, чи слід відхиляти нульову гіпотезу про частку населення.

Отже, залежно від значення статистики перевірки гіпотези для пропорції та рівня значущості нульова гіпотеза відхиляється або приймається.

Зауважте, що перевірка гіпотез також може називатися протиставленням гіпотез, перевіркою гіпотез або перевіркою значущості.

Формула перевірки гіпотези пропорції

Статистика перевірки гіпотези для частки дорівнює різниці у вибірковій частці мінус запропоноване значення частки, поділене на стандартне відхилення частки.

Таким чином , формула гіпотези перевірки для пропорції :

$\displaystyle Z=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}$

золото:

$Z$

це статистика перевірки гіпотези для частки.
$\widehat{p}$

є пропорцією зразка.
$p$

є значення запропонованої пропорції.
$n$

це розмір вибірки.
$\displaystyle\sqrt{\frac{p(1-p)}{n}}$

є стандартним відхиленням пропорції.

Майте на увазі, що недостатньо обчислити статистику перевірки гіпотези для пропорції, але результат потрібно інтерпретувати:

Якщо перевірка гіпотези пропорції є двосторонньою, нульова гіпотеза відхиляється, якщо абсолютне значення статистики перевищує критичне значення Z _α/2 .
Якщо перевірка гіпотези пропорції збігається з правим хвостом, нульова гіпотеза відхиляється, якщо статистичне значення перевищує критичне значення Z _α .
Якщо перевірка гіпотези для пропорції збігається з лівим хвостом, нульова гіпотеза відхиляється, якщо статистика менша за критичне значення -Z _α .

$\begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

Пам’ятайте, що критичні значення можна легко отримати з таблиці нормального розподілу.

➤ Див.: Таблиця нормального розподілу

Приклад перевірки гіпотези на пропорцію

Коли ми побачимо визначення перевірки гіпотези на пропорції та її формулу, ми розв’яжемо приклад, щоб краще зрозуміти концепцію.

За словами виробника, ефективність препарату проти певного захворювання становить 70%. У лабораторії ми перевіряємо ефективність цього препарату, оскільки дослідники вважають, що пропорція інша. Для цього препарат випробовують на 1000 пацієнтів і 641 людина вилікувалась. Виконайте перевірку гіпотези щодо частки населення з рівнем значущості 5%, щоб відхилити або відхилити гіпотезу дослідників.

У цьому випадку нульова гіпотеза та альтернативна гіпотеза перевірки гіпотези для частки сукупності:

$\begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}$

Частка людей у вибірці, які вилікувалися за допомогою препарату, становить:

$\widehat{p}=\cfrac{641}{1000}=0,641$

Ми обчислюємо статистику перевірки гіпотези для пропорції, застосовуючи наведену вище формулу:

$\begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}$

З іншого боку, оскільки рівень значущості становить 0,05 і це двостороння перевірка гіпотези, критичне значення перевірки становить 1,96.

$Z_{0,025}=1,96$

➤ Див.: Рівень значимості 0,05

Підсумовуючи, абсолютне значення тестової статистики перевищує критичне значення, тому ми відхиляємо нульову гіпотезу та приймаємо альтернативну гіпотезу.

$|-4,07|=4,07>1,96 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”424″ style=”vertical-align: -5px;”></p> </p> <div style=$ ➤ Див.: Перевірка гіпотези для середнього значення

Перевірка гіпотези для двох вибіркових пропорцій

Перевірка гіпотези для пропорцій двох вибірок використовується для відхилення або прийняття нульової гіпотези про те, що пропорції двох різних сукупностей рівні.

Таким чином, нульова гіпотеза перевірки гіпотези для пропорцій двох вибірок завжди:

$H_0: p_1=p_2$

Тоді як альтернативною гіпотезою може бути один із трьох варіантів:

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.

А формула для обчислення статистики перевірки гіпотези для двох вибіркових пропорцій така:

$\displaystyle Z=\frac{\displaystyle \frac{x_1}{n_1}-\frac{x_2}{n_2}}{\displaystyle \sqrt{p(1-p)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$

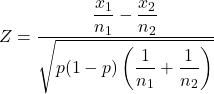
золото:

$Z$

це статистика перевірки гіпотези для пропорцій двох вибірок.
$x_1$

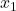
це кількість результатів у зразку 1.
$x_2$

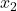
кількість результатів у зразку 2.
$n_1$

розмір вибірки 1.
$n_2$

розмір вибірки 2.
$p$

це сукупна частка двох зразків.

Перевірка гіпотези для k пропорцій вибірки

У перевірці гіпотези щодо пропорцій k вибірок мета полягає в тому, щоб визначити, чи всі пропорції різних популяцій є рівними, або, навпаки, чи існують різні пропорції. Отже, нульова гіпотеза та альтернативна гіпотеза в цьому випадку:

$\begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}$

У цьому випадку сукупна частка всіх зразків розраховується наступним чином:

$p=\cfrac{\displaystyle\sum_{i=1}^k x_i}{\displaystyle\sum_{i=1}^k n_i}=\cfrac{x_1+x_2+\dots+x_k}{n_1+n_2+\dots+n_k}$

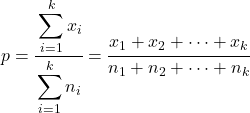
Формула для знаходження статистики перевірки гіпотези для k пропорцій вибірки:

$\displaystyle \chi^2 =\sum_{i=1}^k \frac{(x_i-e_i)^2}{e_i}$

$\displaystyle\chi^2 = \frac{(x_1-e_1)^2}{e_1} +\frac{(x_2-e_2)^2}{e_2} +\dots+\frac{(x_k-e_k)^2}{e_k}$

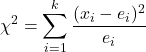
золото:

$\chi^2$

це статистика перевірки гіпотези для k пропорцій вибірки. У цьому випадку статистика відповідає розподілу хі-квадрат.
$x_i$

кількість результатів у вибірці i.
$n_i$

це розмір вибірки i.
$p$

це сукупна частка всіх зразків.
$e_i$

кількість звернень, очікуваних від вибірки i. Розраховується шляхом множення комбінованої пропорції

$p$

за розміром вибірки

$n_i$

.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке перевірка гіпотези щодо пропорції?

Формула перевірки гіпотези пропорції

Приклад перевірки гіпотези на пропорцію

Перевірка гіпотези для двох вибіркових пропорцій

Перевірка гіпотези для k пропорцій вибірки

Про автора

Редакція

Додати коментар