Як перевірити нормальність у r (4 методи)

Багато статистичних тестів припускають , що набори даних розподілені нормально.

Є чотири поширені способи перевірити це припущення в R:

1. (Наочний метод) Створіть гістограму.

• Якщо гістограма приблизно має форму дзвона, то дані вважаються нормально розподіленими.

2. (Візуальний метод) Створіть діаграму QQ.

• Якщо точки на графіку лежать приблизно вздовж прямої діагональної лінії, то дані вважаються нормально розподіленими.

3. (Формальний статистичний тест) Виконайте тест Шапіро-Вілка.

• Якщо p-значення тесту більше α = 0,05, то дані вважаються нормально розподіленими.

4. (Формальний статистичний тест) Виконайте критерій Колмогорова-Смирнова.

• Якщо p-значення тесту більше α = 0,05, то дані вважаються нормально розподіленими.

Наступні приклади показують, як використовувати кожен із цих методів на практиці.

Спосіб 1: Створення гістограми

Наступний код показує, як створити гістограму для нормально розподіленого та ненормально розподіленого набору даних у R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

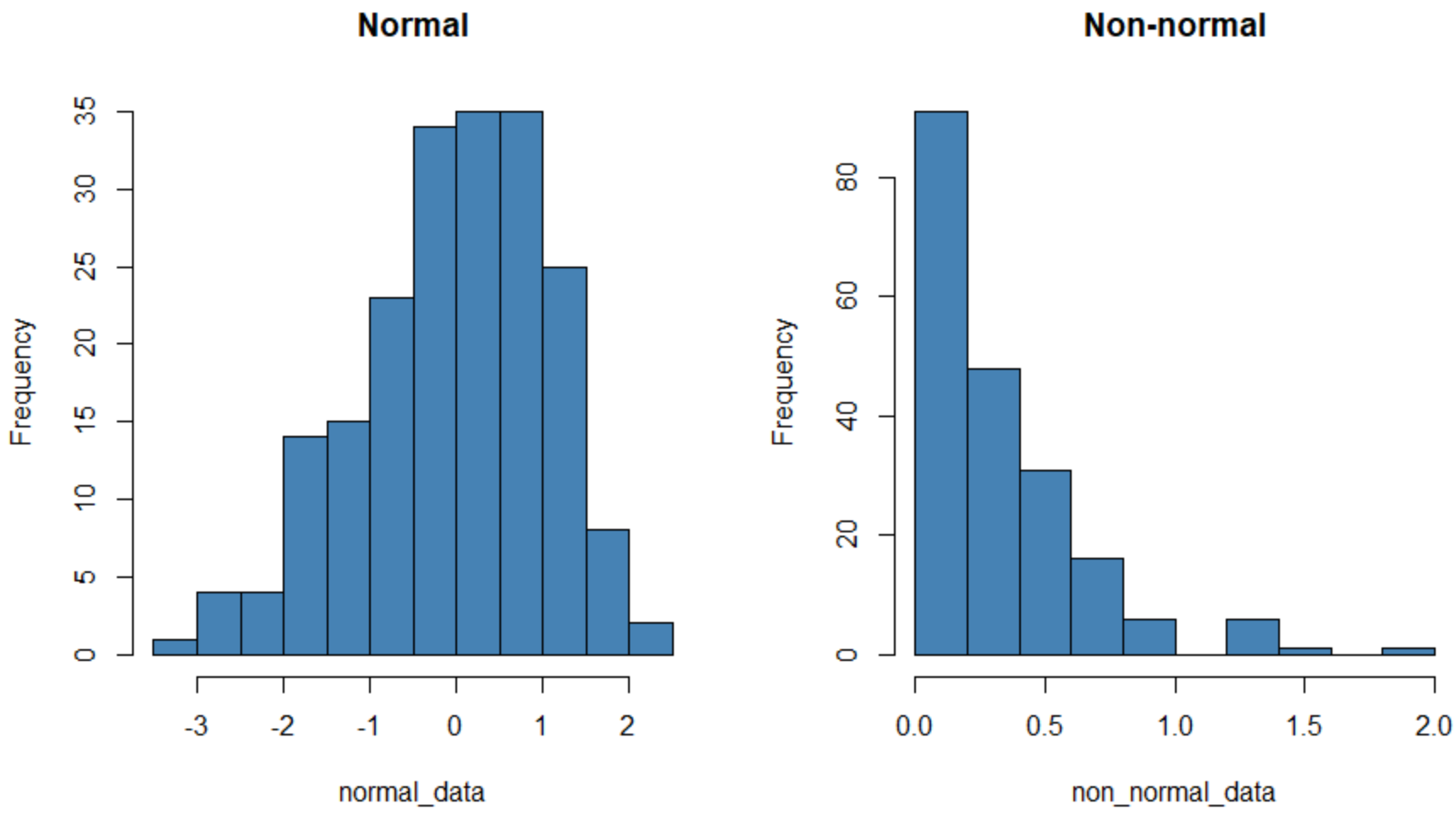
Гістограма ліворуч показує набір даних із нормальним розподілом (приблизно у формі дзвоника), а гістограма праворуч показує набір даних, який розподілено ненормально.

Спосіб 2: Створення графіка QQ

Наступний код показує, як створити діаграму QQ для нормально розподіленого та ненормально розподіленого набору даних у R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

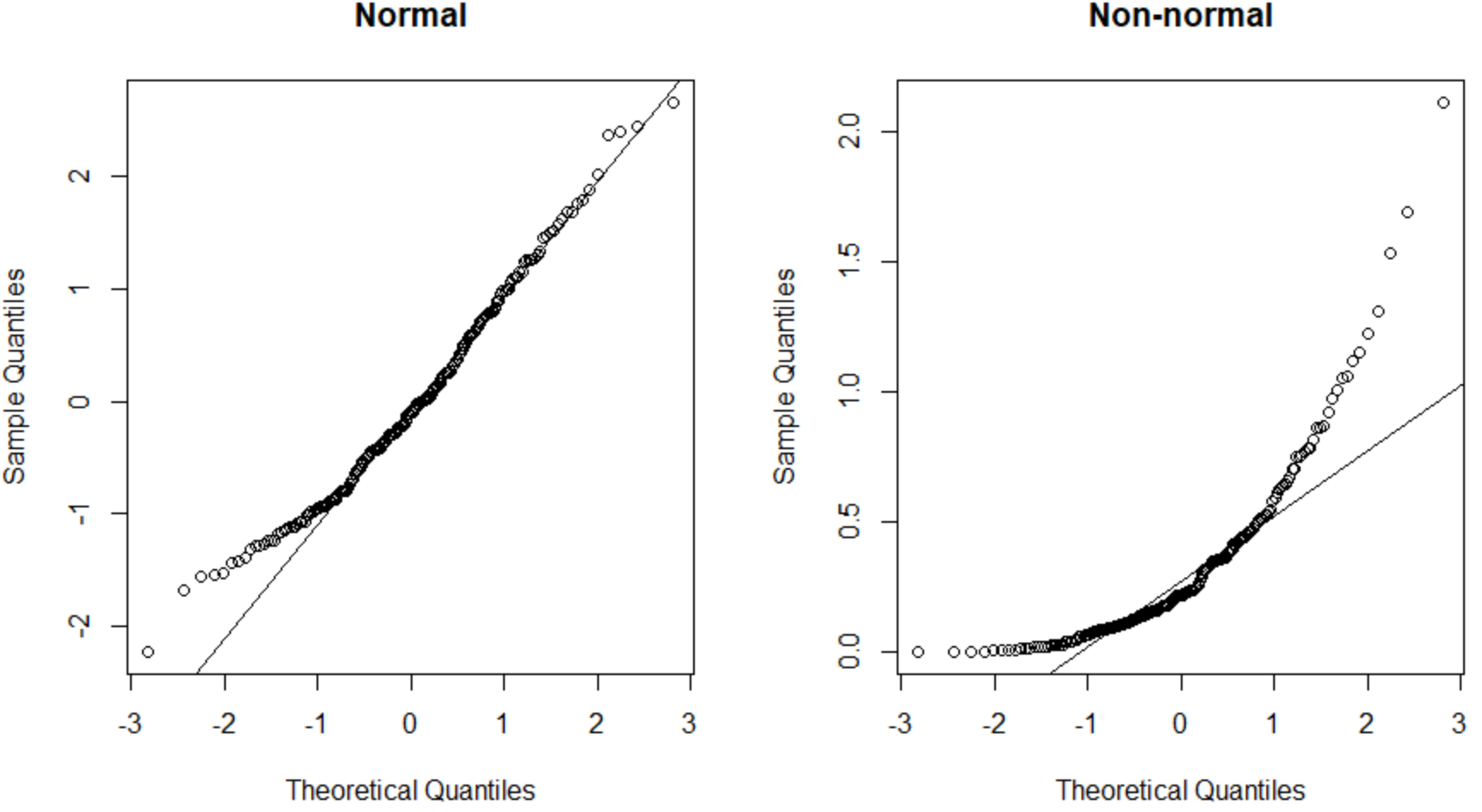
Діаграма QQ ліворуч представляє набір даних із нормальним розподілом (точки розташовані вздовж прямої діагональної лінії), а діаграма QQ праворуч представляє набір даних, який не є нормально розподіленим.

Спосіб 3: Виконайте тест Шапіро-Вілка

Наступний код показує, як виконати тест Шапіро-Вілка на нормально розподіленому та ненормально розподіленому наборі даних у R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

P-значення першого тесту становить не менше 0,05, що вказує на те, що дані розподілені нормально.

Р-значення другого тесту менше 0,05, що вказує на те, що дані не розподілені нормально.

Спосіб 4: Виконайте тест Колмогорова-Смирнова

Наступний код показує, як виконати тест Колмогорова-Смірнова на нормально розподіленому та ненормально розподіленому наборі даних у R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

P-значення першого тесту становить не менше 0,05, що вказує на те, що дані розподілені нормально.

P-значення другого тесту менше 0,05, що вказує на те, що дані не розподілені нормально.

Як обробляти нестандартні дані

Якщо заданий набір даних не розподілений нормально, ми часто можемо виконати одне з наступних перетворень, щоб зробити його більш нормально розподіленим:

1. Перетворення журналу: перетворення значень x в log(x) .

2. Перетворення квадратного кореня: перетворення значень x на √x .

3. Перетворення кубічного кореня: перетворення значень x на x ^1/3 .

Виконуючи ці перетворення, набір даних зазвичай стає більш нормально розподіленим.

Прочитайте цей посібник , щоб дізнатися, як виконати ці перетворення в R.

Додаткові ресурси

Як створити гістограми в R
Як створити та інтерпретувати діаграму QQ у R
Як виконати тест Шапіро-Вілка в R
Як виконати пробу Колмогорова-Смирнова в Р