Що таке переобладнання в машинному навчанні? (пояснення та приклади)

У машинному навчанні ми часто створюємо моделі, щоб ми могли робити точні прогнози щодо певних явищ.

Наприклад, припустімо, що ми хочемо створити регресійну модель , яка використовує прогностичну змінну години, витрачені на навчання , щоб передбачити оцінку ACT змінної відповіді для старшокласників.

Щоб створити цю модель, ми зберемо дані про години, витрачені на навчання, і відповідний бал ACT для сотень учнів у певному шкільному окрузі.

Потім ми використаємо ці дані для навчання моделі, яка може робити прогнози щодо балів, які отримає певний учень, на основі загальної кількості вивчених годин.

Щоб оцінити корисність моделі, ми можемо виміряти, наскільки прогнози моделі відповідають спостережуваним даним. Одним із найбільш часто використовуваних показників для цього є середня квадратична помилка (MSE), яка обчислюється таким чином:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

золото:

• n: загальна кількість спостережень
• y _i : значення відповіді ^i-го спостереження
• f(x _i ): прогнозоване значення відповіді i- ^го спостереження

Чим ближче прогнози моделі до спостережень, тим нижчим буде MSE.

Однак одна з найбільших помилок машинного навчання полягає в оптимізації моделей для зменшення MSE навчання , тобто того, наскільки добре прогнози моделі відповідають даним, які ми використовували для навчання моделі.

Коли модель надто зосереджена на зниженні MSE навчання, вона часто працює надто важко, щоб знайти закономірності в даних навчання, які просто викликані випадковістю. Тоді, коли модель застосовується до невидимих даних, її продуктивність є низькою.

Це явище відоме як переобладнання . Це трапляється, коли ми «підганяємо» модель занадто близько до навчальних даних і, таким чином, створюємо модель, яка не є корисною для прогнозування на нових даних.

Приклад переобладнання

Щоб зрозуміти переобладнання, давайте повернемося до прикладу створення регресійної моделі, яка використовує години, витрачені на навчання , щоб передбачити оцінку ACT .

Припустімо, ми збираємо дані для 100 учнів у певному шкільному окрузі та створюємо швидку діаграму розсіювання, щоб візуалізувати зв’язок між двома змінними:

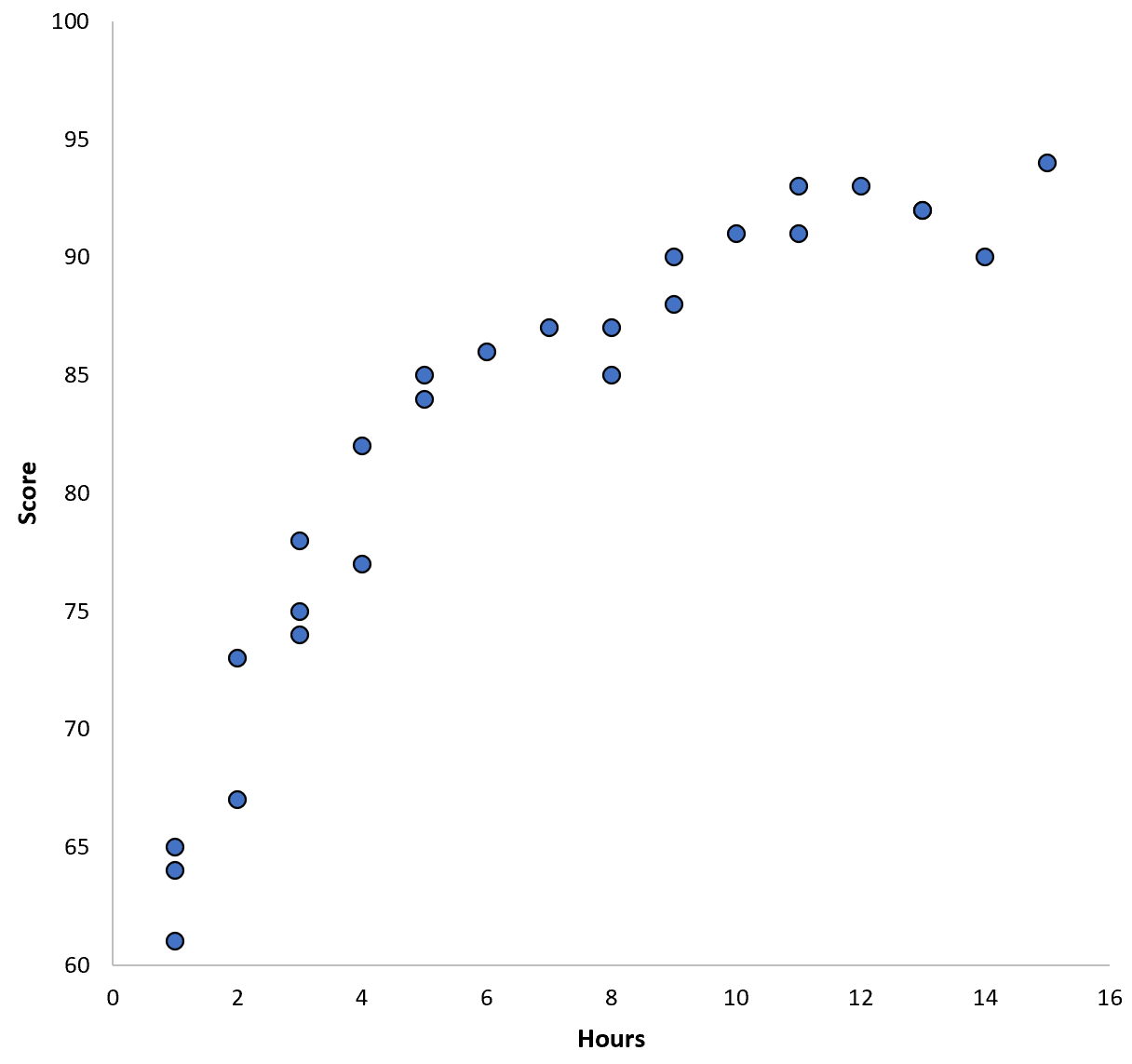
Зв’язок між двома змінними видається квадратичним, тож припустімо, що ми застосуємо наступну модель квадратичної регресії:

Оцінка = 60,1 + 5,4*(годин) – 0,2*(годин) ²

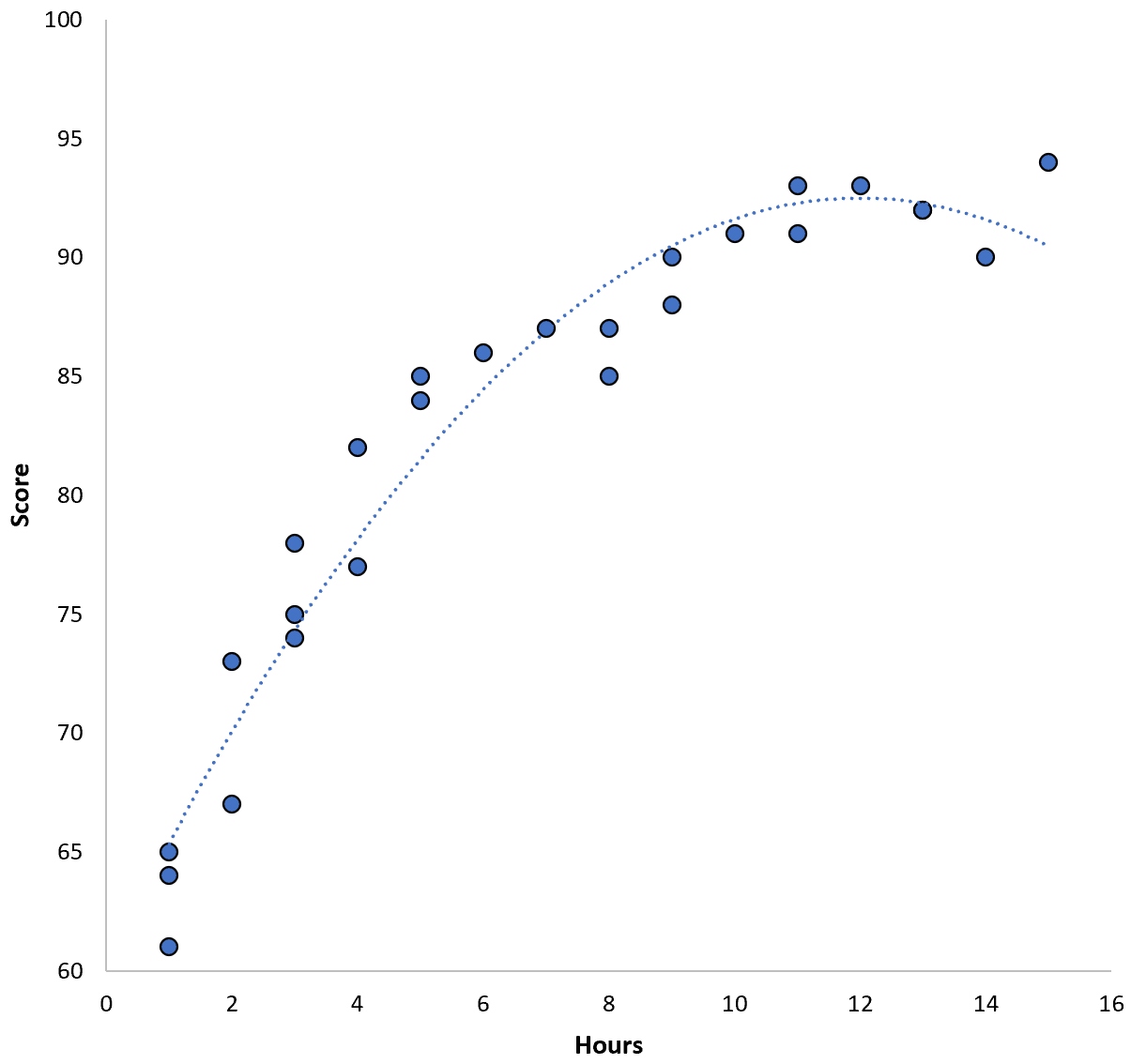
Ця модель має навчальну середньоквадратичну помилку (MSE) 3,45 . Тобто середньоквадратична різниця між прогнозами, зробленими моделлю, і фактичними балами ACT становить 3,45.

Однак ми могли б зменшити цю навчальну MSE, підібравши поліноміальну модель вищого порядку. Наприклад, припустимо, що ми застосовуємо таку модель:

Оцінка = 64,3 – 7,1*(годин) + 8,1*(годин) ² – 2,1*(годин) ³ + 0,2*(годин ^{) 4 – 0,1*(годин) 5 +} 0,2(годин) ⁶

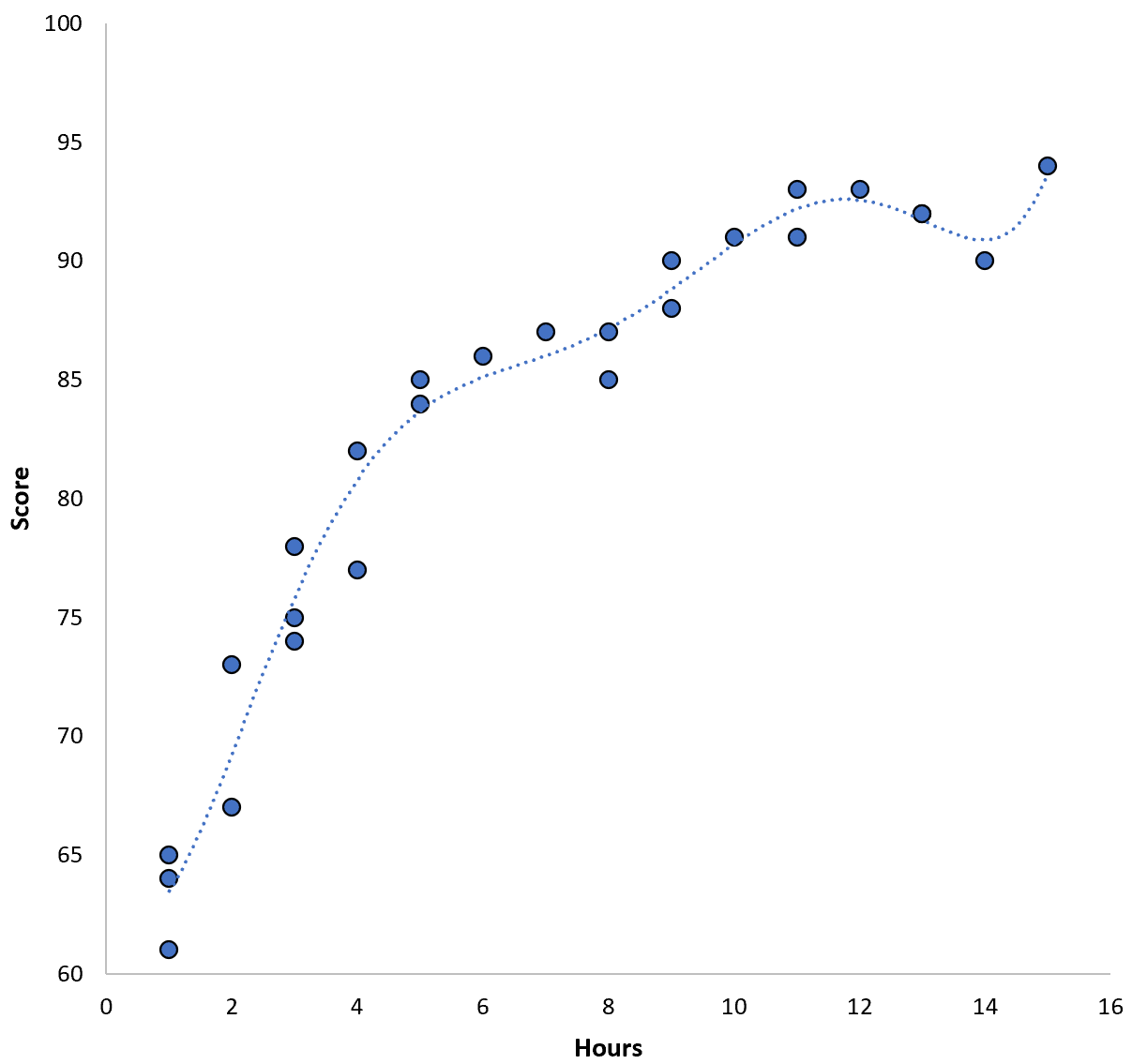
Зверніть увагу, як лінія регресії набагато точніше відповідає фактичним даним, ніж попередня лінія регресії.

Ця модель має тренувальну середньоквадратичну помилку (MSE) лише 0,89 . Тобто середньоквадратична різниця між прогнозами, зробленими моделлю, і фактичними показниками ACT становить 0,89.

Ця підготовка MSE набагато менша, ніж у попередній моделі.

Однак нам не дуже важлива навчальна MSE , тобто те, наскільки добре прогнози моделі відповідають даним, які ми використовували для навчання моделі. Натомість ми в основному дбаємо про тест MSE – MSE, коли наша модель застосовується до невидимих даних.

Якщо ми застосували наведену вище модель поліноміальної регресії вищого порядку до невидимого набору даних, вона, швидше за все, працюватиме гірше, ніж простіша модель квадратичної регресії. Тобто це дасть вищий тест MSE, а це саме те, чого ми не хочемо.

Як виявити та уникнути переобладнання

Найпростіший спосіб виявити переобладнання — виконати перехресну перевірку. Найпоширеніший метод відомий як k-кратна перехресна перевірка , і він працює таким чином:

Крок 1. Випадково розділіть набір даних на k груп або «згорток» приблизно однакового розміру.

Крок 2. Виберіть одну зі складок як комплект для утримання. Відрегулюйте шаблон до решти k-1 складок. Розрахуйте випробування MSE на основі спостережень у шарі, який був натягнутий.

Крок 3. Повторіть цей процес k разів, кожного разу використовуючи інший набір як набір виключень.

Крок 4: Обчисліть загальну MSE тесту як середнє значення k MSE тесту.

Тест MSE = (1/k)*ΣMSE _i

золото:

• k: кількість згинів
• MSE _i : Перевірте MSE на ^i-й ітерації

Цей тест MSE дає нам гарне уявлення про те, як дана модель працюватиме на невідомих даних.

На практиці ми можемо підібрати кілька різних моделей і виконати k-кратну перехресну перевірку кожної моделі, щоб дізнатися її тест MSE. Тоді ми можемо вибрати модель з найнижчим тестом MSE як найкращу модель для використання для прогнозування в майбутньому.

Це гарантує, що ми виберемо модель, яка, ймовірно, найкраще працюватиме з майбутніми даними, на відміну від моделі, яка просто мінімізує навчальний MSE і добре «підходить» до історичних даних.

Додаткові ресурси

Що таке компроміс зміщення та дисперсії в машинному навчанні?
Вступ до K-кратної перехресної перевірки
Регресійні та класифікаційні моделі в машинному навчанні