Як перетворити дані в r (логарифм, квадратний корінь, кубічний корінь)

Багато статистичних тестів припускають, що залишки змінної відповіді розподілені нормально.

Однак залишки часто розподіляються неправильно . Один із способів вирішення цієї проблеми полягає в перетворенні змінної відповіді за допомогою одного з трьох перетворень:

1. Перетворення журналу: перетворення змінної відповіді з y на log(y) .

2. Перетворення квадратного кореня: перетворення змінної відповіді з y на √y .

3. Перетворення кубічного кореня: перетворення змінної відповіді з y на y ^1/3 .

Виконуючи ці перетворення, змінна відповіді загалом наближається до нормального розподілу. Наступні приклади показують, як виконати ці перетворення в R.

Перетворення журналу в R

Наступний код показує, як виконати перетворення журналу змінної відповіді:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

Наступний код показує, як створити гістограми для відображення розподілу y до та після виконання перетворення журналу:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

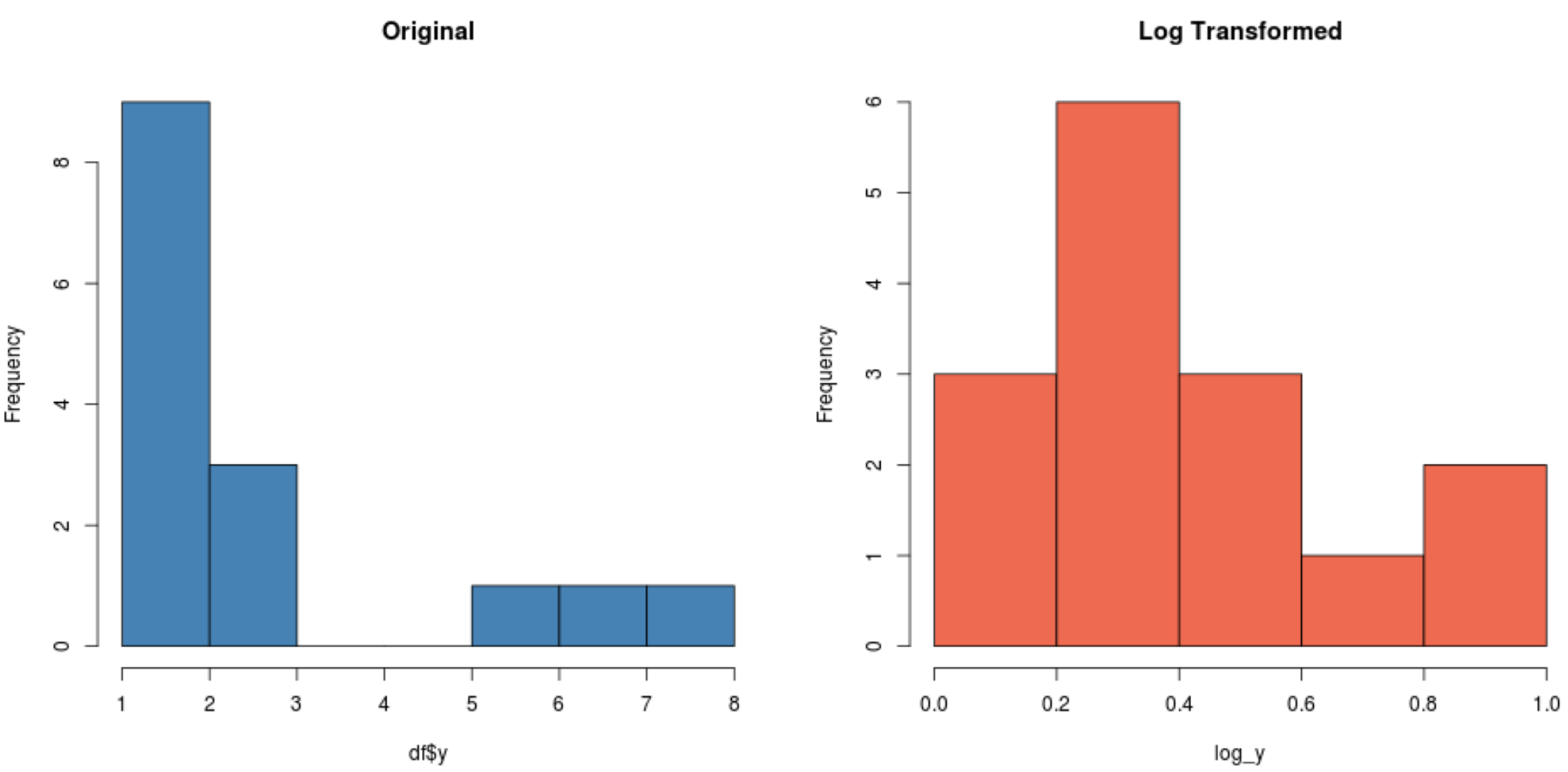
Зверніть увагу, що логарифмічно перетворений розподіл є набагато більш нормальним, ніж вихідний розподіл. Це все ще не ідеальна «форма дзвона», але вона ближча до нормального розподілу, ніж оригінальний розподіл.

Насправді, якщо ми виконаємо тест Шапіро-Вілка для кожного розподілу, ми виявимо, що вихідний розподіл не відповідає припущенню про нормальність, тоді як логарифмічний розподіл – ні (при α = 0,05):

 #perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data: df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:log_y
W = 0.89089, p-value = 0.06917

Перетворення квадратного кореня в R

Наступний код показує, як виконати перетворення квадратного кореня для змінної відповіді:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

Наступний код показує, як створити гістограми для відображення розподілу y до та після виконання перетворення квадратного кореня:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed') 

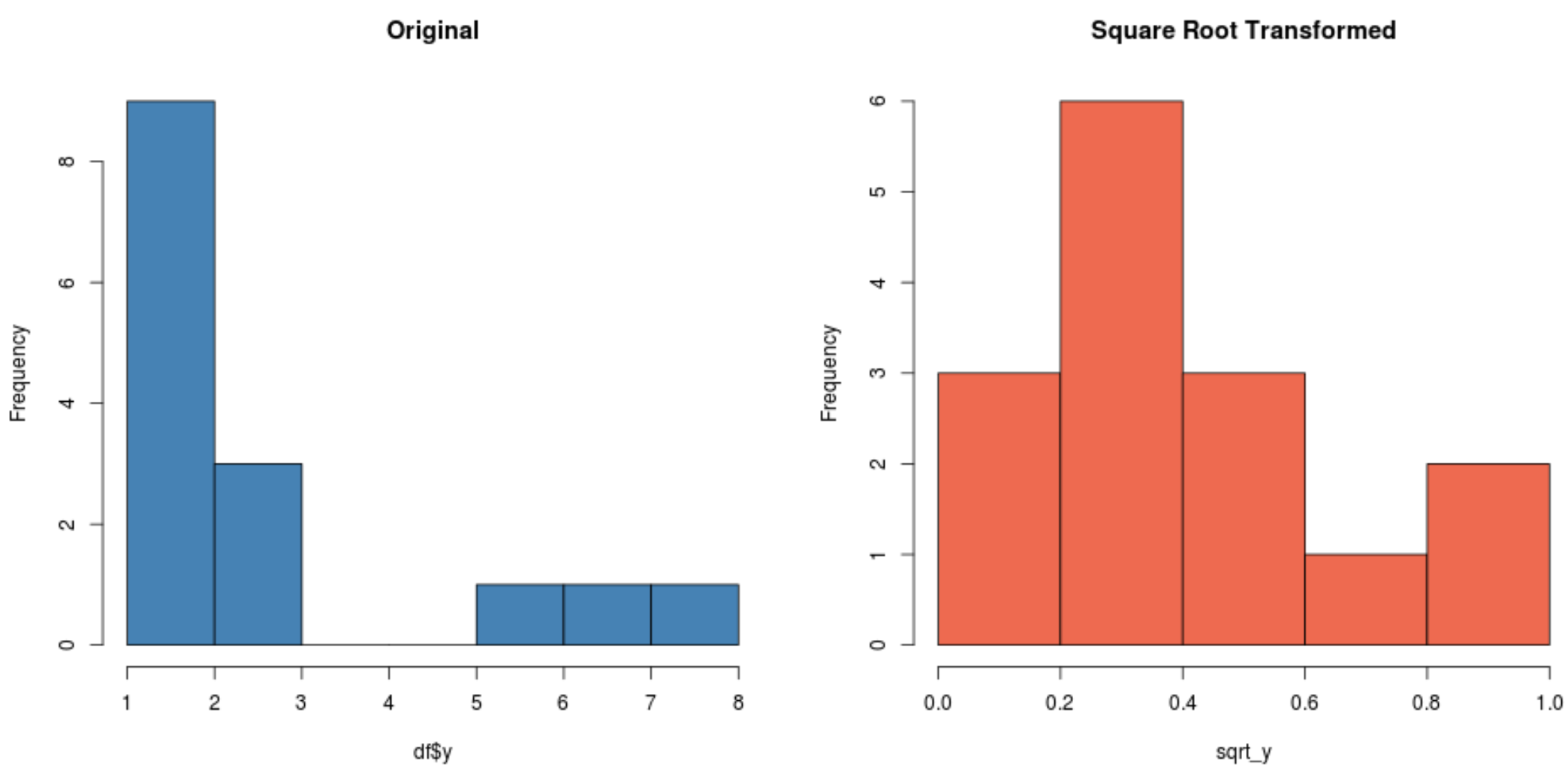
Зверніть увагу на те, що перетворений розподіл квадратного кореня має набагато більш нормальний розподіл, ніж вихідний розподіл.

Перетворення кубічного кореня в R

Наступний код показує, як виконати перетворення кубічного кореня для змінної відповіді:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

Наступний код показує, як створити гістограми для відображення розподілу y до та після виконання перетворення квадратного кореня:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed') 

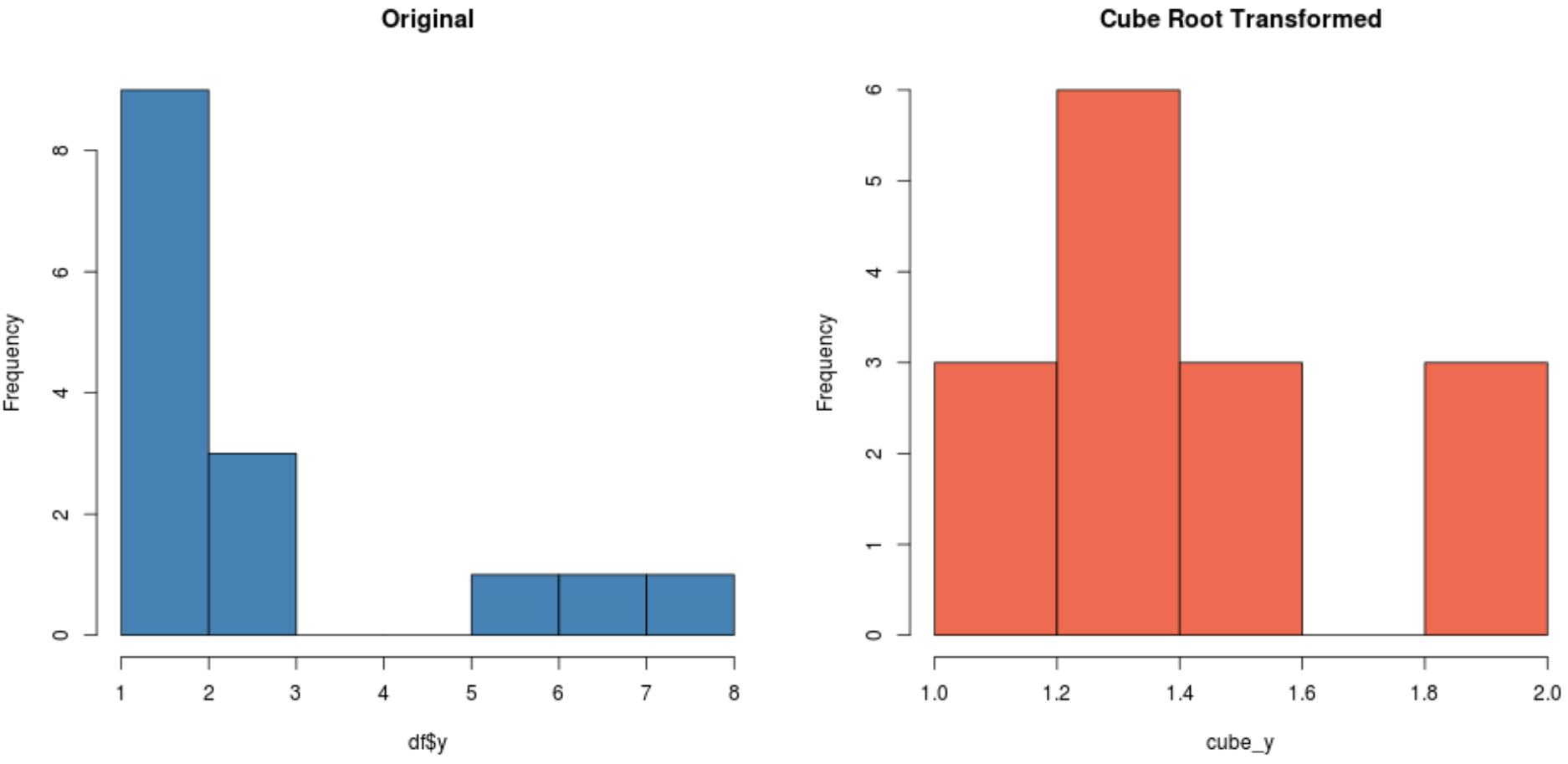
Залежно від вашого набору даних одне з цих перетворень може створити новий набір даних, розподілений більш нормально, ніж інші.