Як виконати дисперсійний аналіз повторних вимірювань у spss

Дисперсійний аналіз із повторними вимірюваннями використовується для визначення того, чи існує статистично значуща різниця між середніми значеннями трьох або більше груп, у кожній з яких є ті самі суб’єкти.

У цьому підручнику пояснюється, як виконати односторонній дисперсійний аналіз повторних вимірювань у SPSS.

Приклад: дисперсійний аналіз повторних вимірювань у SPSS

Дослідники хочуть знати, чи чотири різні препарати викликають різний час реакції. Щоб перевірити це, вони виміряли час реакції п’яти пацієнтів на чотири різні препарати. Оскільки кожен пацієнт вимірюється на кожному з чотирьох препаратів, ми використовуватимемо дисперсійний аналіз повторних вимірювань, щоб визначити, чи відрізняється середній час реакції між препаратами.

Виконайте наступні кроки, щоб виконати повторні вимірювання ANOVA у SPSS.

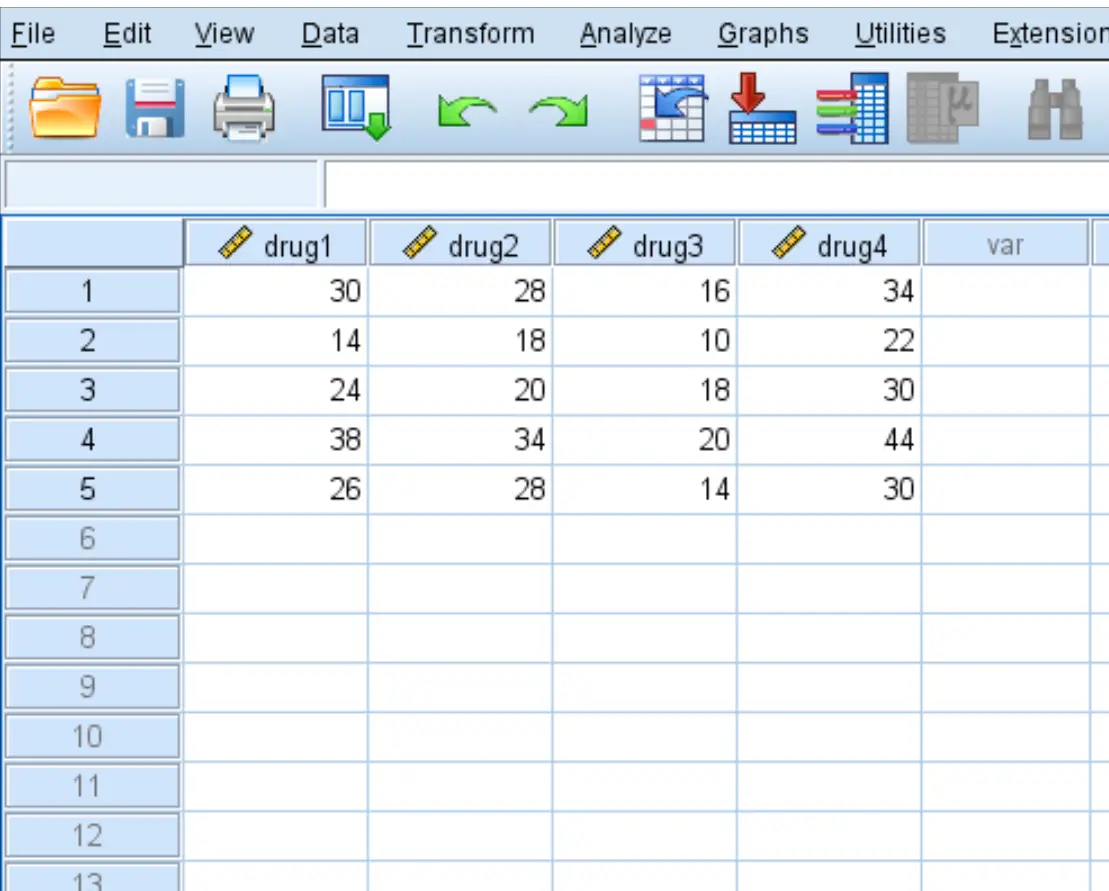
Крок 1: Введіть дані.

Введіть такі дані, які показують час реакції (у секундах) п’яти пацієнтів на чотири ліки:

Крок 2: Виконайте повторний аналіз ANOVA.

Натисніть вкладку «Аналіз» , потім «Загальна лінійна модель» , потім «Повторні вимірювання» :

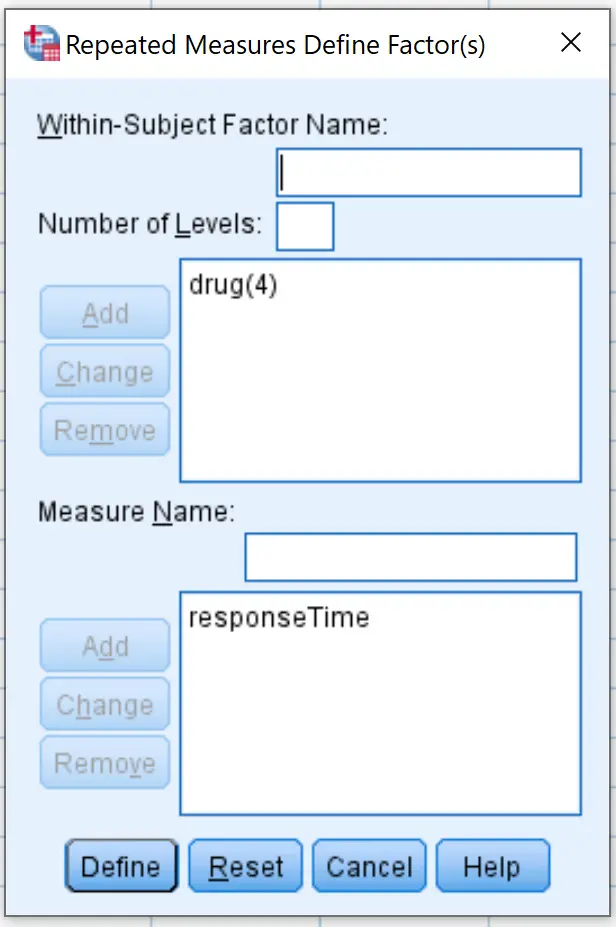
У новому вікні, що з’явиться, введіть назву препарату для внутрішньосуб’єктного фактора. Введіть 4 для кількості рівнів (оскільки кожен досліджуваний тестував 4 різні препарати), а потім натисніть «Додати» . Введіть ResponseTime для Measure Name , а потім натисніть Add . Нарешті натисніть «Установити» .

У новому вікні, що з’явиться, перетягніть кожну з чотирьох змінних препарату в область, позначену як Змінні суб’єкта :

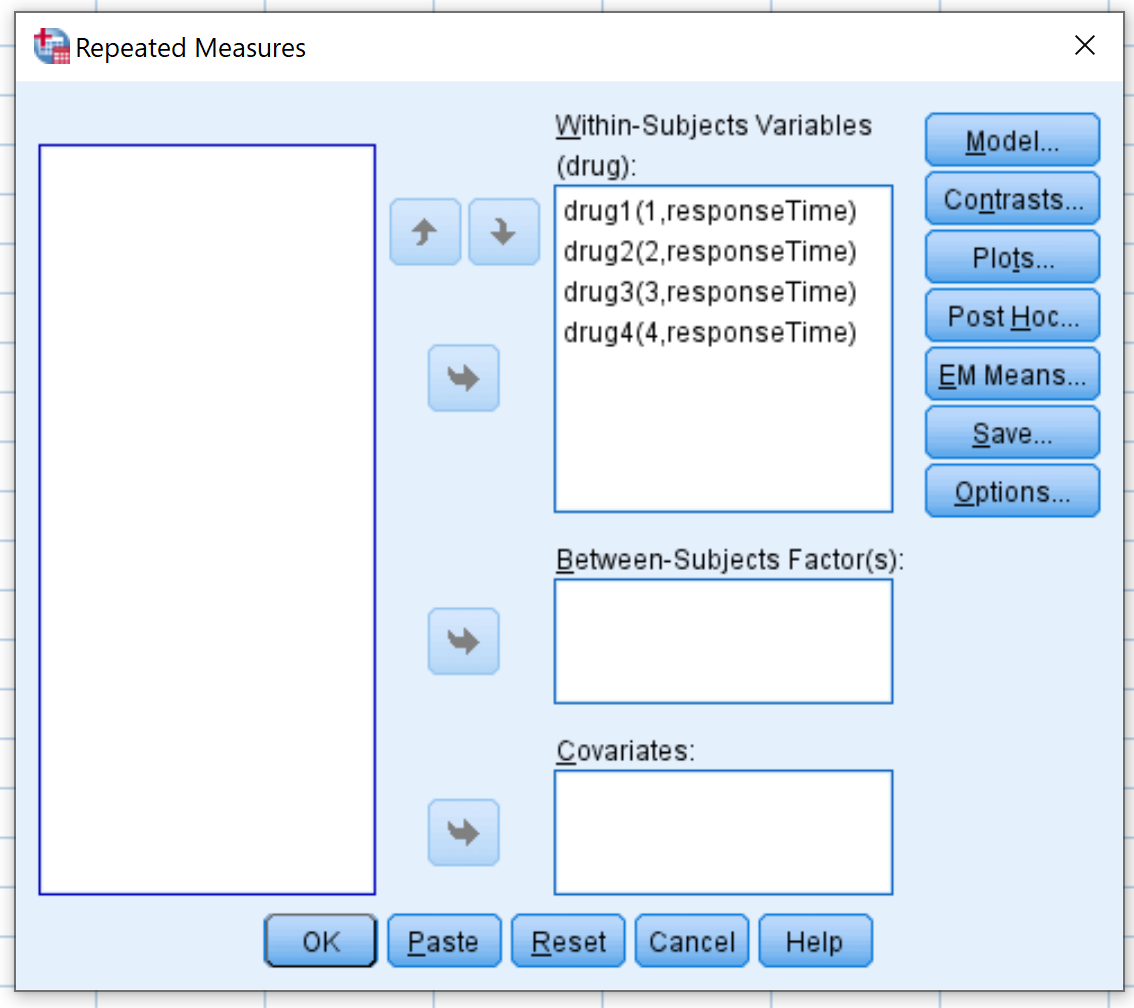
Далі натисніть «Ділянки» . Перетягніть змінний препарат у область, позначену Горизонтальна вісь . Потім натисніть Додати . Потім натисніть Продовжити .

Далі натисніть EM Means . Перетягніть змінну препарату в поле з написом «Показати засоби для» . Потім поставте прапорець біля пункту «Порівняти основні ефекти» та виберіть «Бонферроні» зі спадного меню. Потім натисніть Продовжити .

Нарешті натисніть OK .

Крок 2: Інтерпретація результатів.

Після натискання кнопки OK з’являться результати повторних вимірювань ANOVA. Ось як інтерпретувати результат:

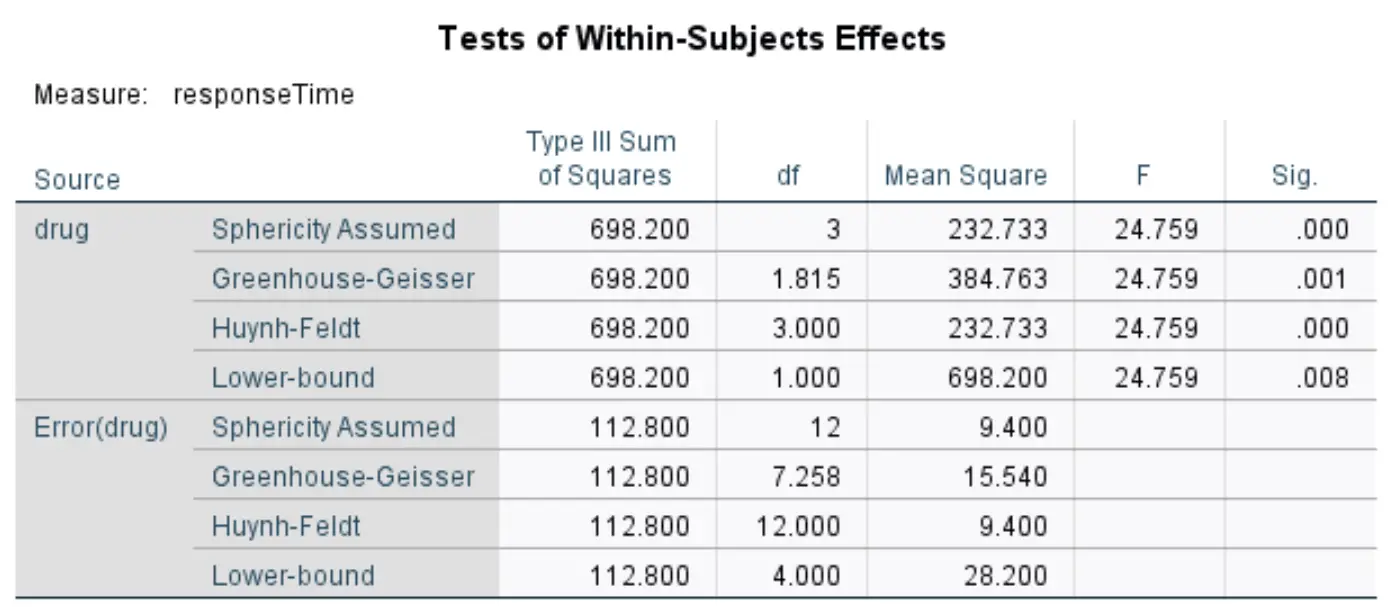
Тести внутрішньосуб’єктних ефектів

У цій таблиці відображається загальна F-статистика та відповідне значення p за результатами повторних вимірювань ANOVA. Зазвичай ми використовуємо значення з рядка з позначкою Greenhouse-Geisser .

Відповідно до цього рядка F-статистика становить 24,759 , а відповідне значення p — 0,001 . Оскільки це p-значення менше 0,05, ми можемо відхилити нульову гіпотезу та зробити висновок, що існує статистично значуща різниця в середньому часі реакції між чотирма препаратами.

Попарні порівняння

Оскільки ми відхилили нульову гіпотезу, це означає, що принаймні два групових середніх різні. Щоб визначити, які групи засобів відрізняються, ми можемо скористатися цією таблицею, яка відображає попарні порівняння між кожним препаратом.

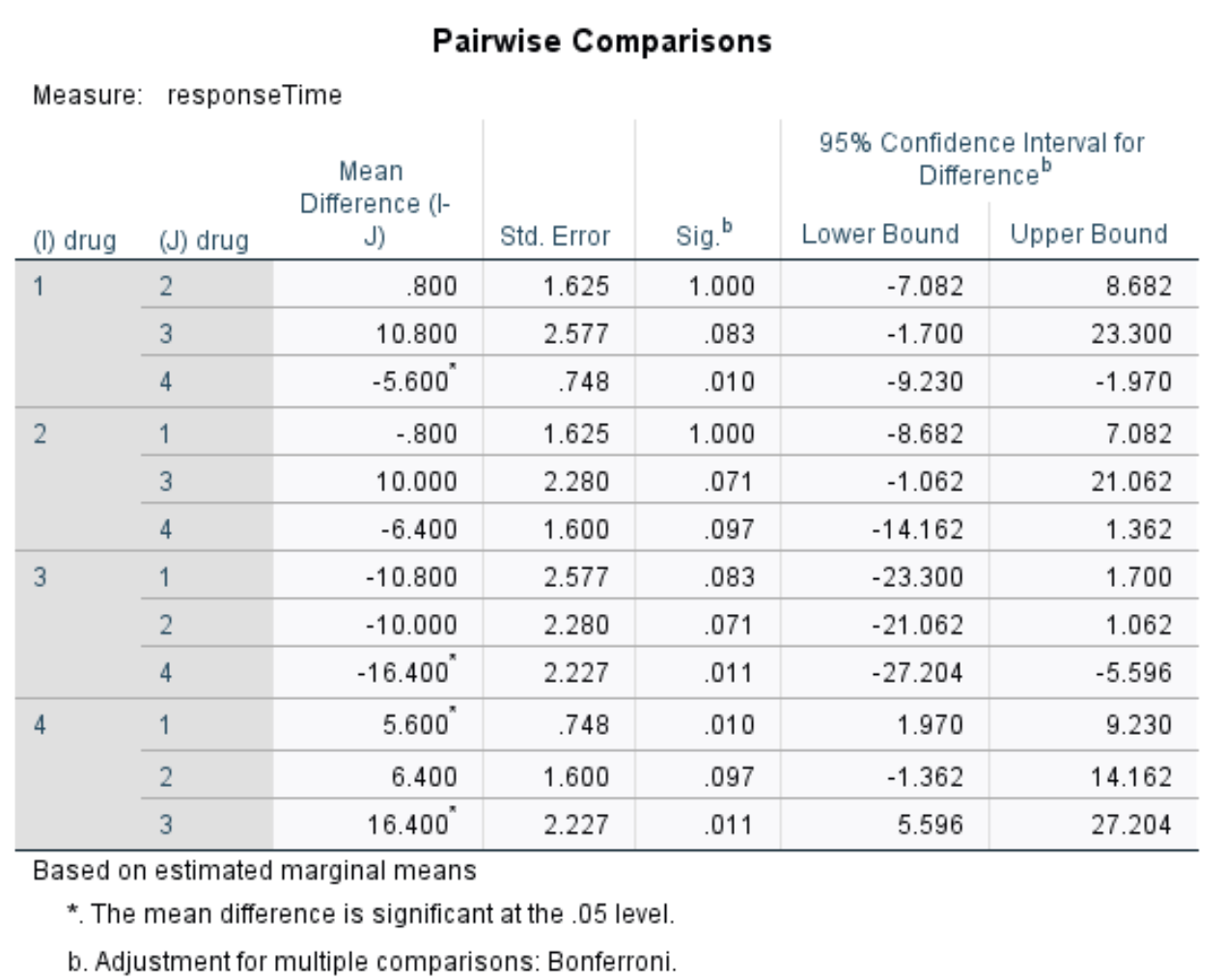
У таблиці ми можемо побачити p-значення для наступних порівнянь:

• препарат 1 проти препарату 2 | р-значення = 1,000
• препарат 1 проти препарату 3 | р-значення = 0,083
• препарат 1 проти препарату 4 | р-значення = 0,010
• препарат 2 проти препарату 3 | р-значення = 0,071
• препарат 2 проти препарату 4 | р-значення = 0,097
• препарат 3 проти препарату 4 | р-значення = 0,011

Єдині значення p менше 0,05 для препарату 1 проти препарату 4 і препарату 3 проти препарату 4. Усі інші порівняння мають значення p більше 0,05.

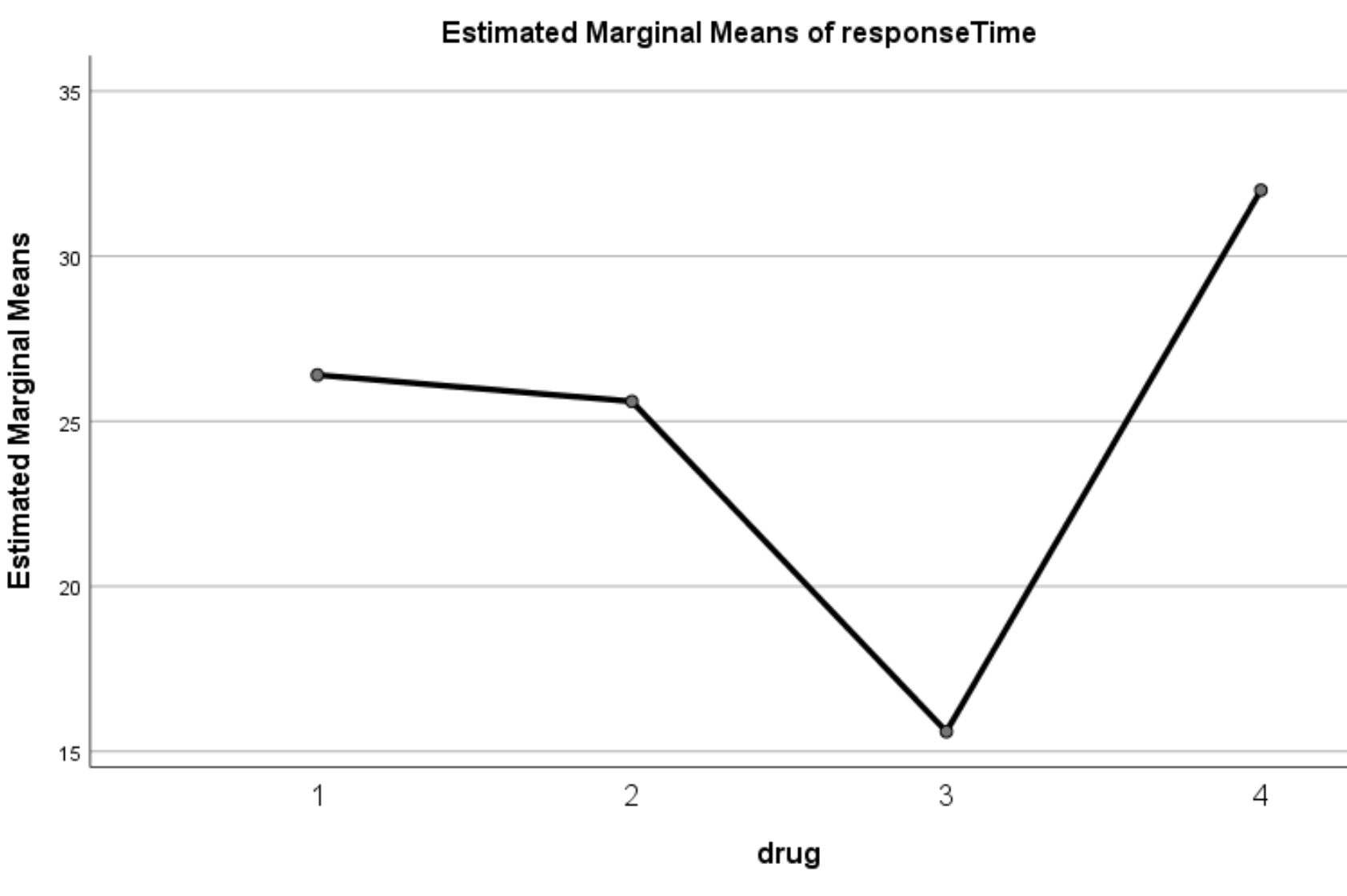
Графік оцінених граничних середніх

Ця діаграма відображає приблизний середній час відповіді для кожного препарату. З графіка ми чітко бачимо, що час відповіді суттєво різнився між чотирма різними препаратами:

Крок 3: Повідомте про результати.

Нарешті, ми можемо повідомити про результати повторних вимірювань ANOVA. Ось приклад того, як це зробити:

Було проведено односторонній повторний аналіз ANOVA, щоб визначити, чи відрізнявся середній час реакції пацієнтів між чотирма різними ліками.

Односторонній ANOVA з повторними вимірюваннями показав, що тип використовуваного препарату призвів до статистично значущих відмінностей у часі відповіді (F = 24,75887, p = 0,001).

Тест Бонферроні для численних порівнянь показав, що існує статистично значуща різниця в часі відповіді між пацієнтами, які приймали препарат 1 і препарат 4, а також препарат 3 і препарат 4.