Як виконати поетапну регресію в sas (з прикладом)

Поетапна регресія – це процедура, яку ми можемо використати для побудови регресійної моделі з набору змінних предикторів шляхом покрокового введення та видалення предикторів у моделі, доки більше не буде статистично обґрунтованої причини для введення або видалити більше.

Метою поетапної регресії є створення регресійної моделі, яка включає всі прогностичні змінні, які статистично значимо пов’язані зі змінною відповіді .

Щоб виконати покрокову регресію в SAS, ви можете використовувати PROC REG з інструкцією SELECTION .

У наступному прикладі показано, як на практиці виконувати поетапну регресію в SAS.

Приклад: виконання покрокової регресії в SAS

Припустімо, що ми маємо такий набір даних у SAS, який містить чотири змінні предиктора (x1, x2, x3, x4) і одну змінну відповіді (y):

 /*create dataset*/
data my_data;
    input x1 x2 x3 x4 y;
    datalines ;
1 4 10 13 78
2 4 12 14 81
5 3 7 10 75
8 2 13 9 97
10 5 12 5 95
14 7 8 6 90
17 8 10 6 86 
19 5 15 5 90
20 5 12 4 93
21 4 10 3 95
;
run ;

/*view dataset*/
proc print data =my_data;

Тепер припустімо, що ми хочемо визначити, яка комбінація змінних предиктора дасть найкращу модель множинної лінійної регресії .

Коли ми говоримо про «найкращу» регресійну модель, ми маємо на увазі модель, яка максимізує або мінімізує певні показники.

Є два показники, які ми зазвичай використовуємо, щоб оцінити, яка модель регресії є найкращою серед групи потенційних моделей:

1. Скоригований R-квадрат : Скоригований R-квадрат показує нам корисність моделі, скоригований на основі кількості предикторів у моделі. Найкращою вважається модель із найвищим скоригованим значенням R-квадрат.

2. AIC : Інформаційний критерій Akaike (AIC) — це показник, який використовується для порівняння відповідності різних регресійних моделей. Найкращою вважається модель з найменшим значенням AIC.

На щастя, ми можемо обчислити як підігнаний R-квадрат, так і значення AIC для регресійних моделей у SAS, використовуючи PROC REG із оператором SELECTION .

Наступний код показує, як це зробити:

 /*perform stepwise multiple linear regression*/
proc reg data =my_data outest =est;
    model y=x1 x2 x3 x4 / selection=adjrsq aic ;
    output out =out p=pr=r;
run ;
quit ; 

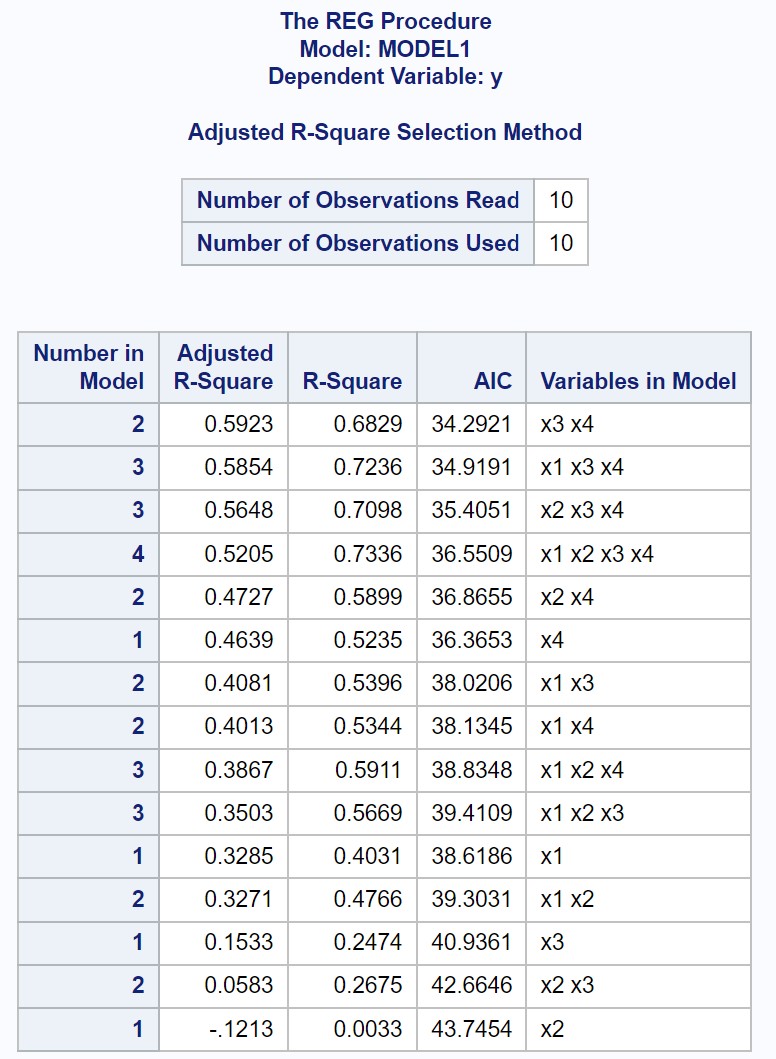
Вихідні дані відображають підібрані значення R-квадрат і AIC для кожної можливої моделі множинної лінійної регресії.

З результату ми бачимо, що значення з найвищим скоригованим значенням R-квадрата та найнижчим значенням AIC є регресійною моделлю, яка використовує лише x3 та x4 як змінні предиктора.

Таким чином, ми заявляємо, що наступна модель є «найкращою» серед усіх можливих моделей:

y = b ₀ + b ₁ (x3) + b ₂ (x4)

Ця модель регресії має такі показники:

• Скориговане значення R-квадрат: 0,5923
• AIC: 34,2921

Примітки щодо вибору «найкращої» моделі регресії

Зауважте, що іноді модель із найвищим скоригованим значенням R-квадрат не завжди має найнижче значення AIC.

Коли справа доходить до прийняття рішення про те, яка модель регресії найкраща, скоригований R-квадрат і AIC служать пропозиціями, але в реальному світі вам може знадобитися використання досвіду домену, щоб визначити, яка модель є найкращою.

Також може бути доцільним вибрати економну модель , тобто модель, яка досягає бажаного рівня відповідності, використовуючи якомога менше змінних предикторів.

Обґрунтування такого типу моделі випливає з ідеї бритви Оккама (іноді її називають «принципом ощадливості»), яка говорить, що найпростіше пояснення, ймовірно, є правильним.

Застосовуючи статистику, слід віддати перевагу моделі, яка має невелику кількість параметрів, але забезпечує задовільний рівень відповідності, аніж моделі, яка має масу параметрів і досягає лише трохи вищого рівня відповідності.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в SAS:

Як виконати просту лінійну регресію в SAS
Як виконати множинну лінійну регресію в SAS
Як виконати поліноміальну регресію в SAS
Як виконати логістичну регресію в SAS