Поліноміальна регресія в google таблицях (крок за кроком)

Регресійний аналіз використовується для кількісного визначення зв’язку між однією або декількома змінними предиктора та змінною відповіді .

Найпоширенішим типом регресійного аналізу є проста лінійна регресія , яка використовується, коли прогностична змінна та змінна відповіді мають лінійний зв’язок.

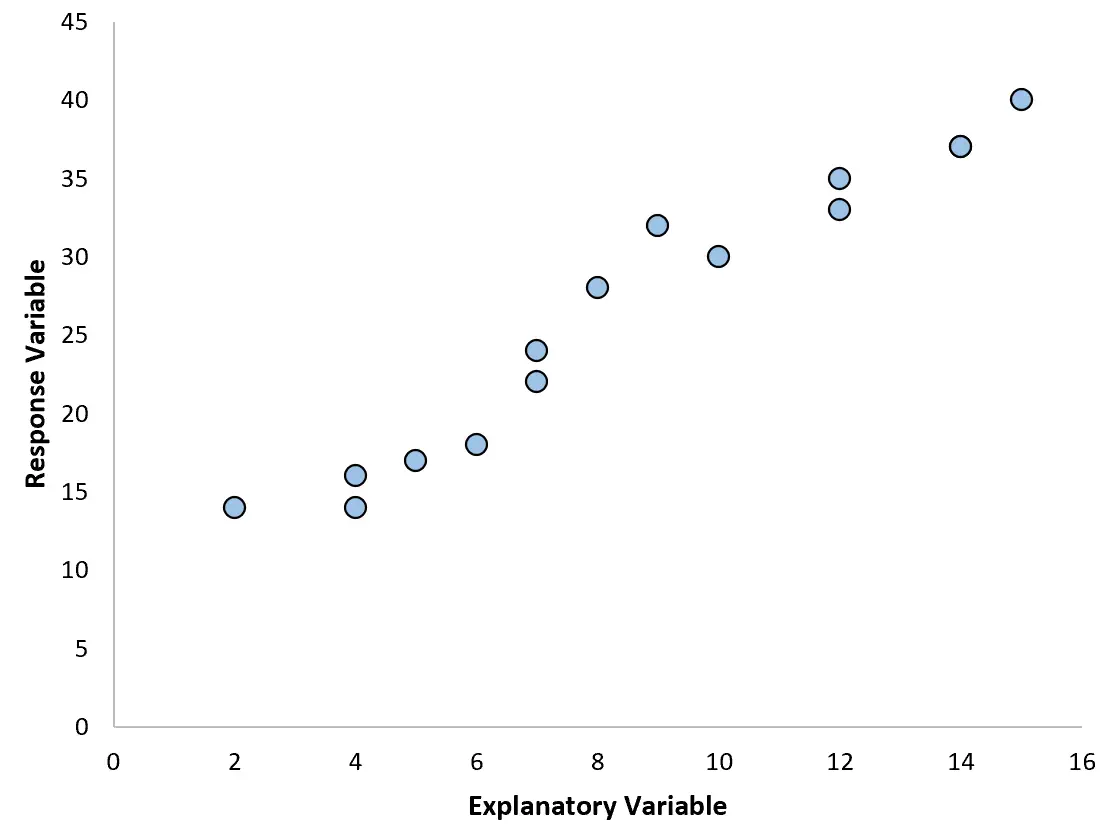
Однак інколи зв’язок між змінною-прогнозом і змінною відповіді є нелінійним.

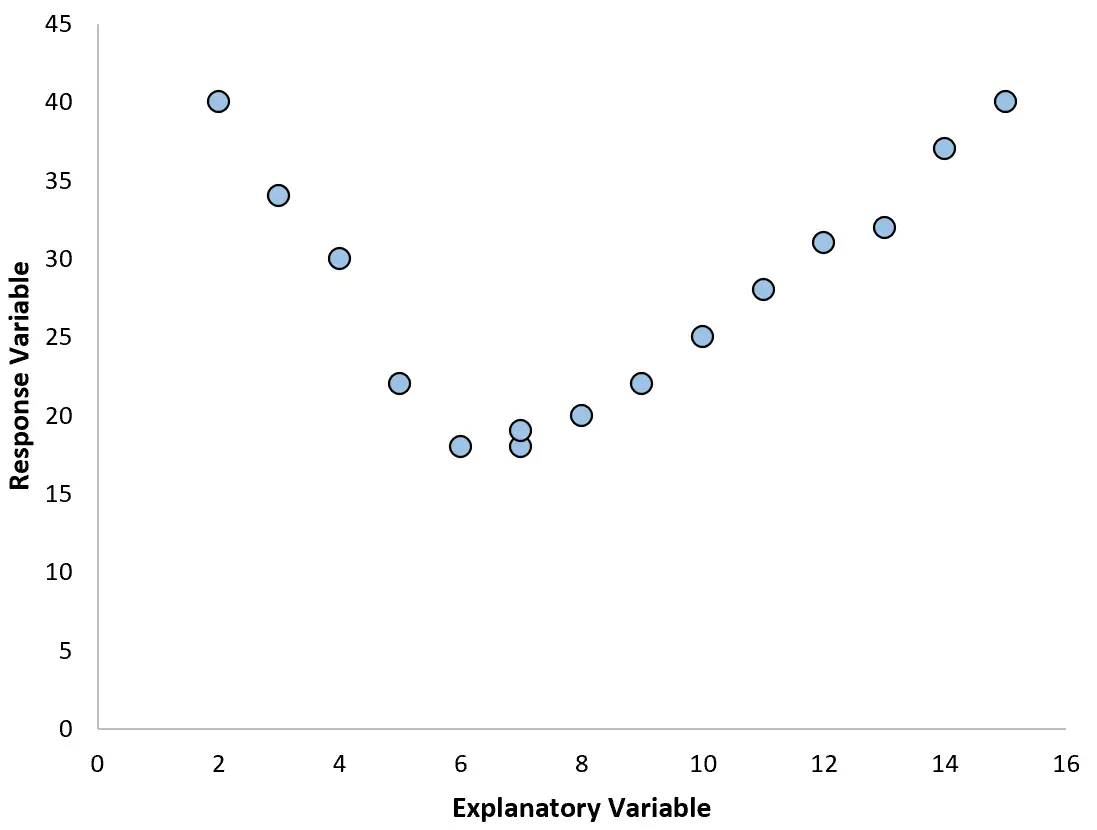
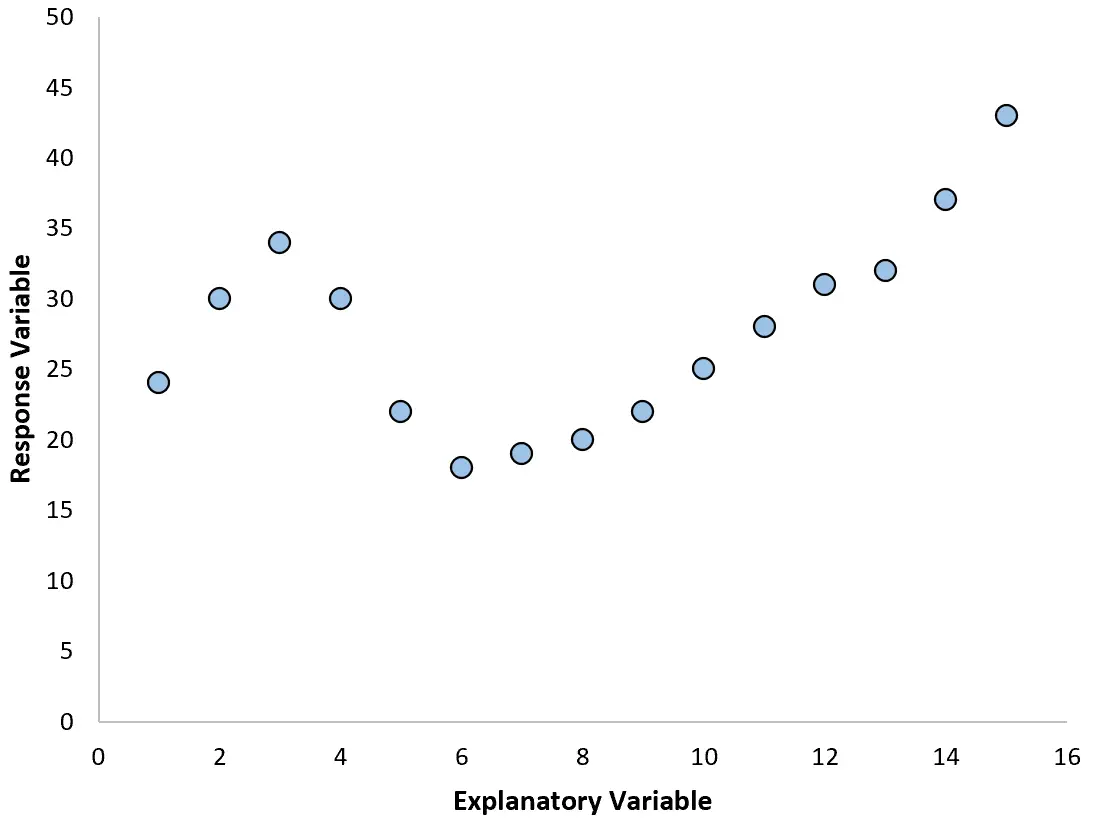
У цих випадках має сенс використовувати поліноміальну регресію , яка може врахувати нелінійний зв’язок між змінними.

У цьому посібнику наведено покроковий приклад виконання поліноміальної регресії в Google Таблицях.

Крок 1: Створіть дані

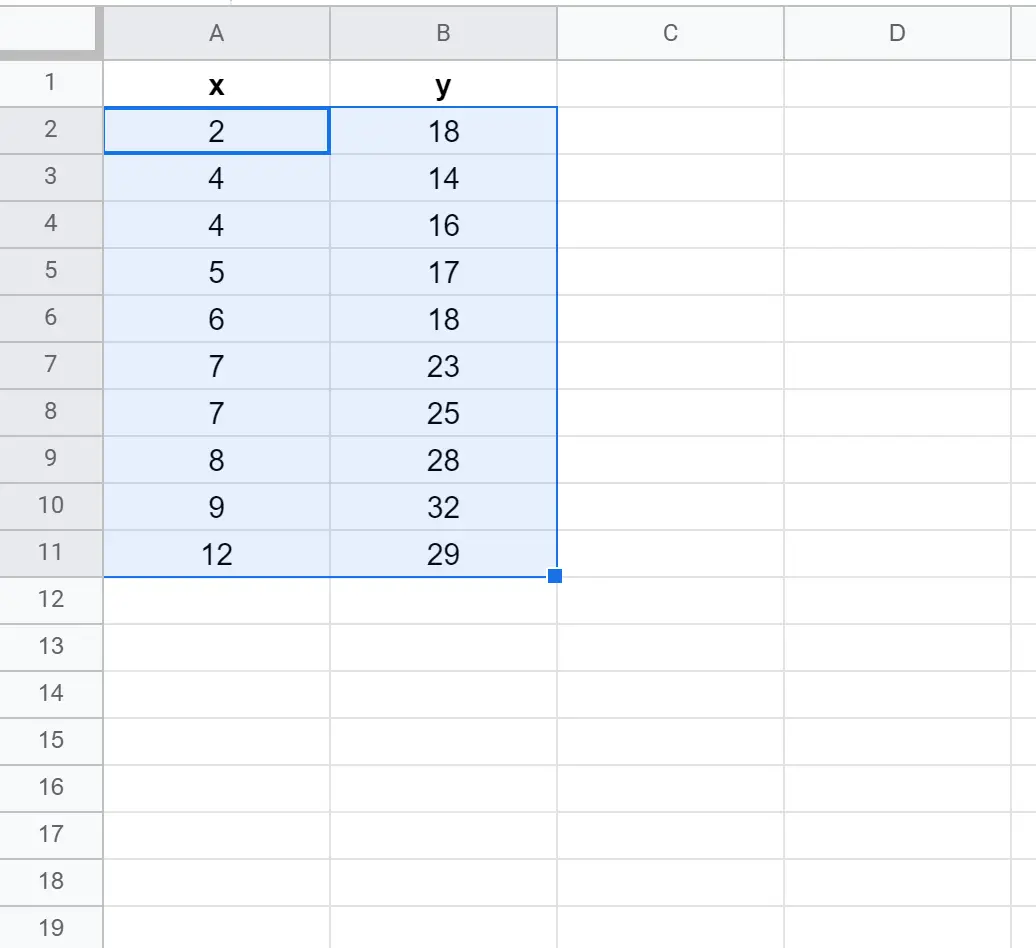
Спочатку давайте створимо фальшивий набір даних із такими значеннями:

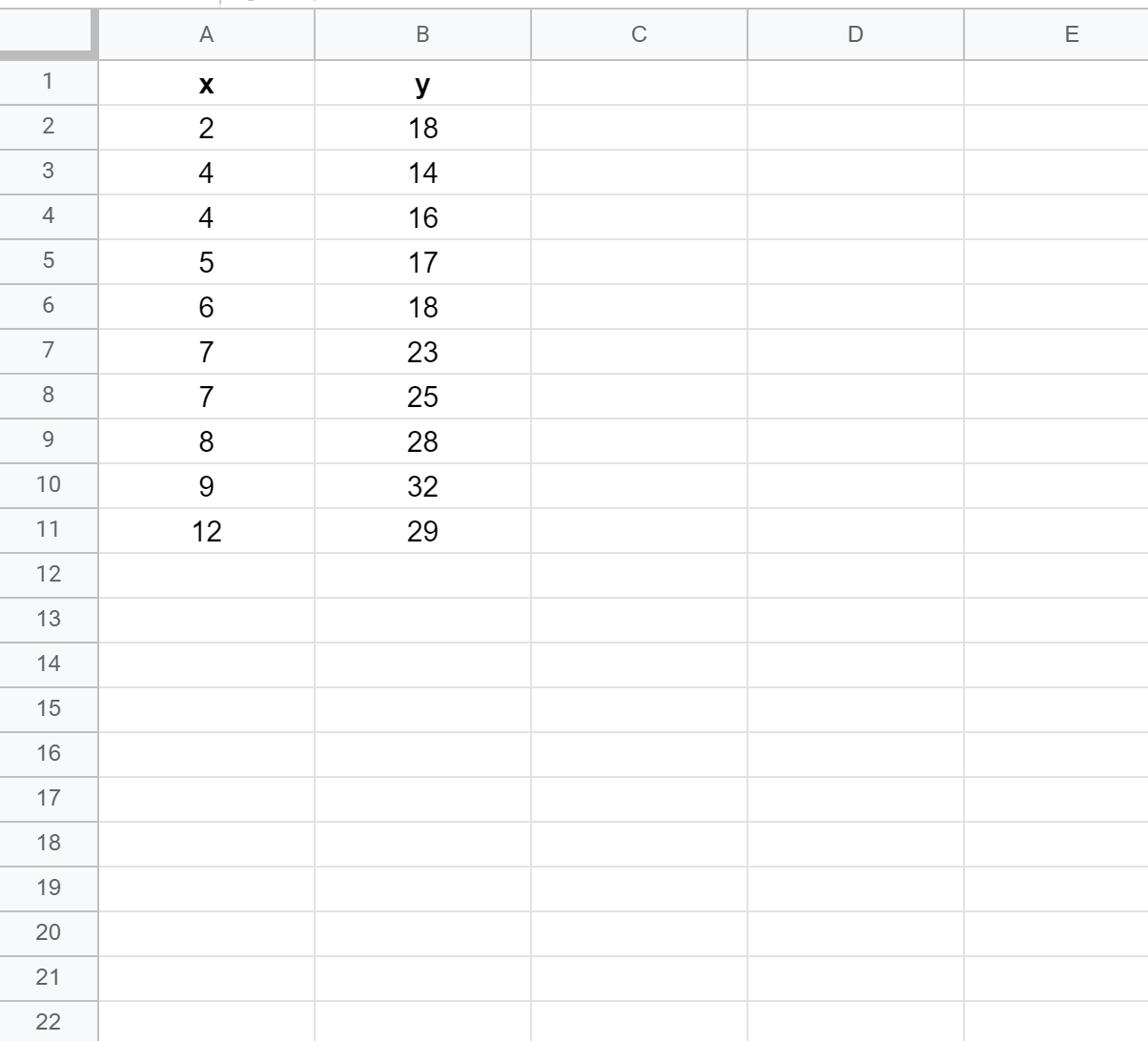
Крок 2: Створіть діаграму розсіювання

Далі ми створимо діаграму розсіювання для візуалізації даних.

Спочатку виділіть клітинки A2:B11 наступним чином:

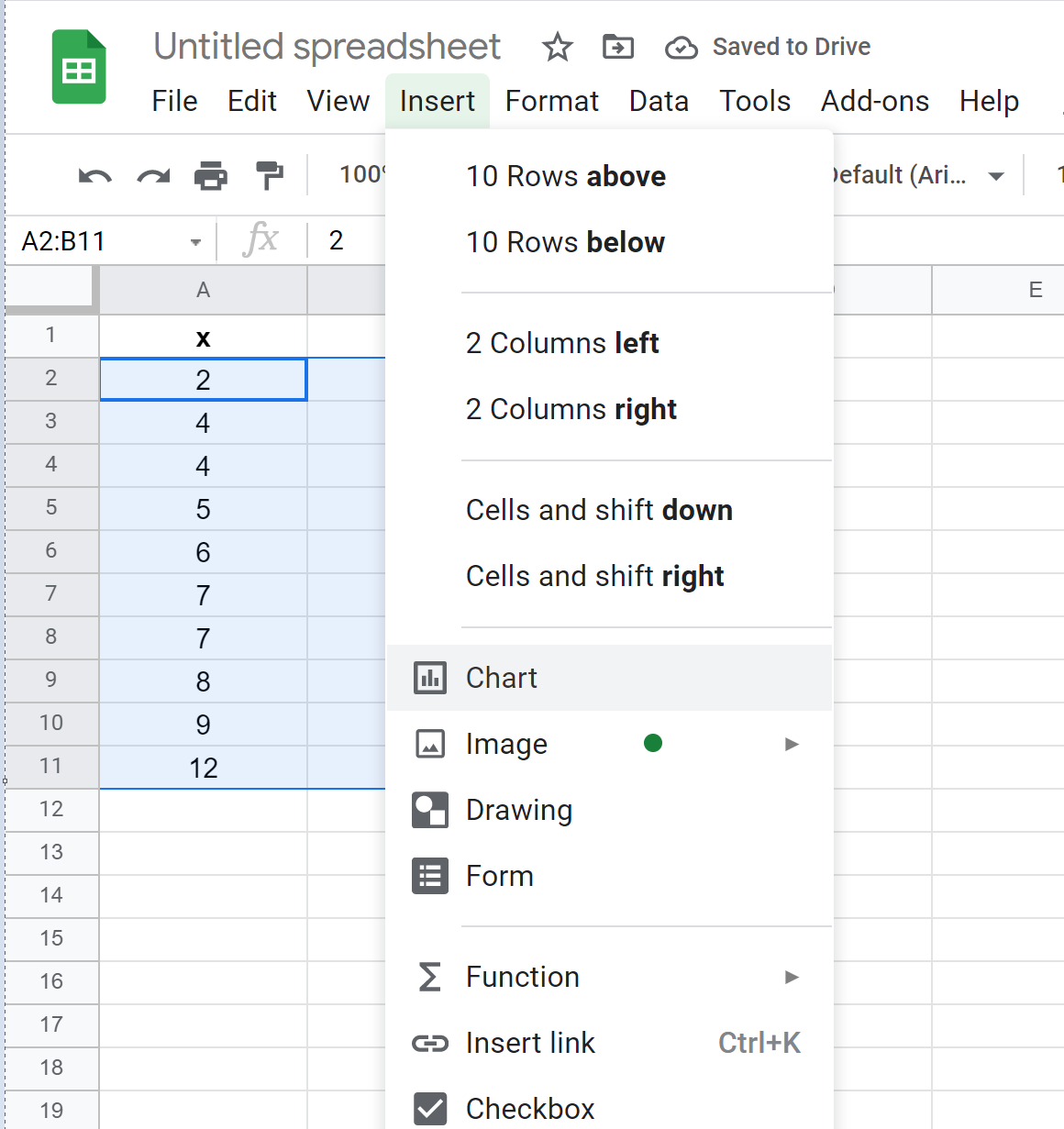
Далі перейдіть на вкладку «Вставлення» , а потім у спадному меню виберіть «Діаграма» .

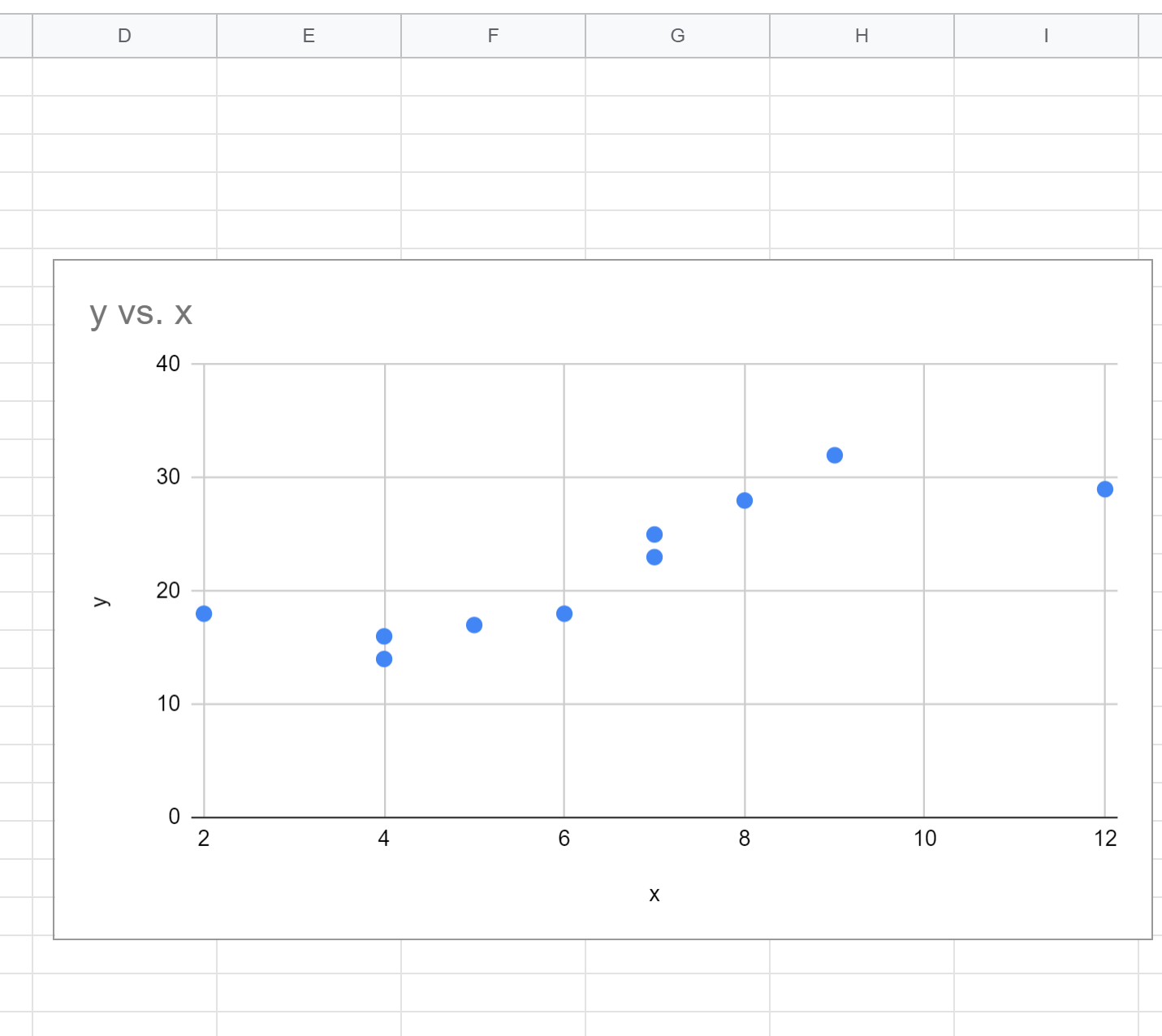
За замовчуванням Google Таблиці вставлять точкову діаграму:

Крок 3: Знайдіть рівняння поліноміальної регресії

Потім двічі клацніть будь-де на діаграмі розсіювання, щоб відобразити вікно редактора графіків праворуч:

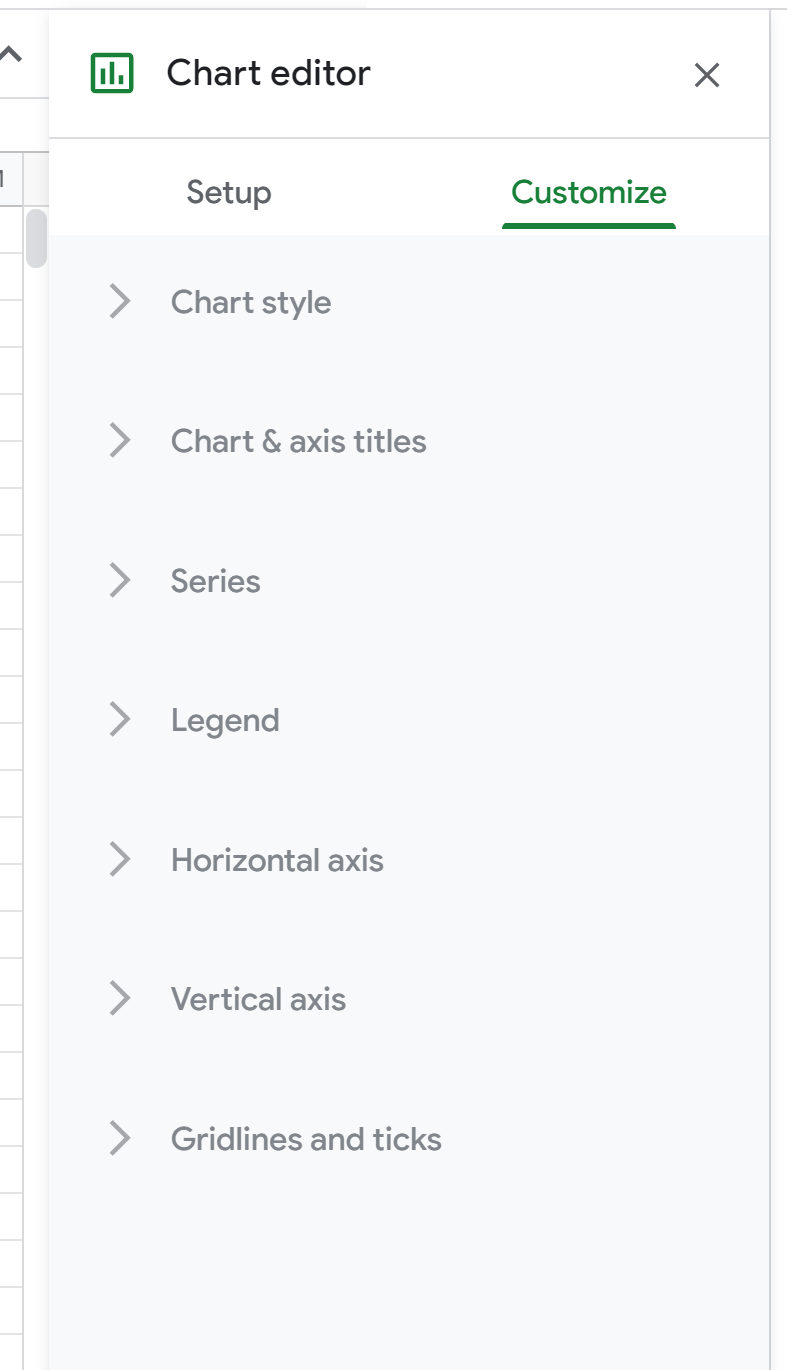
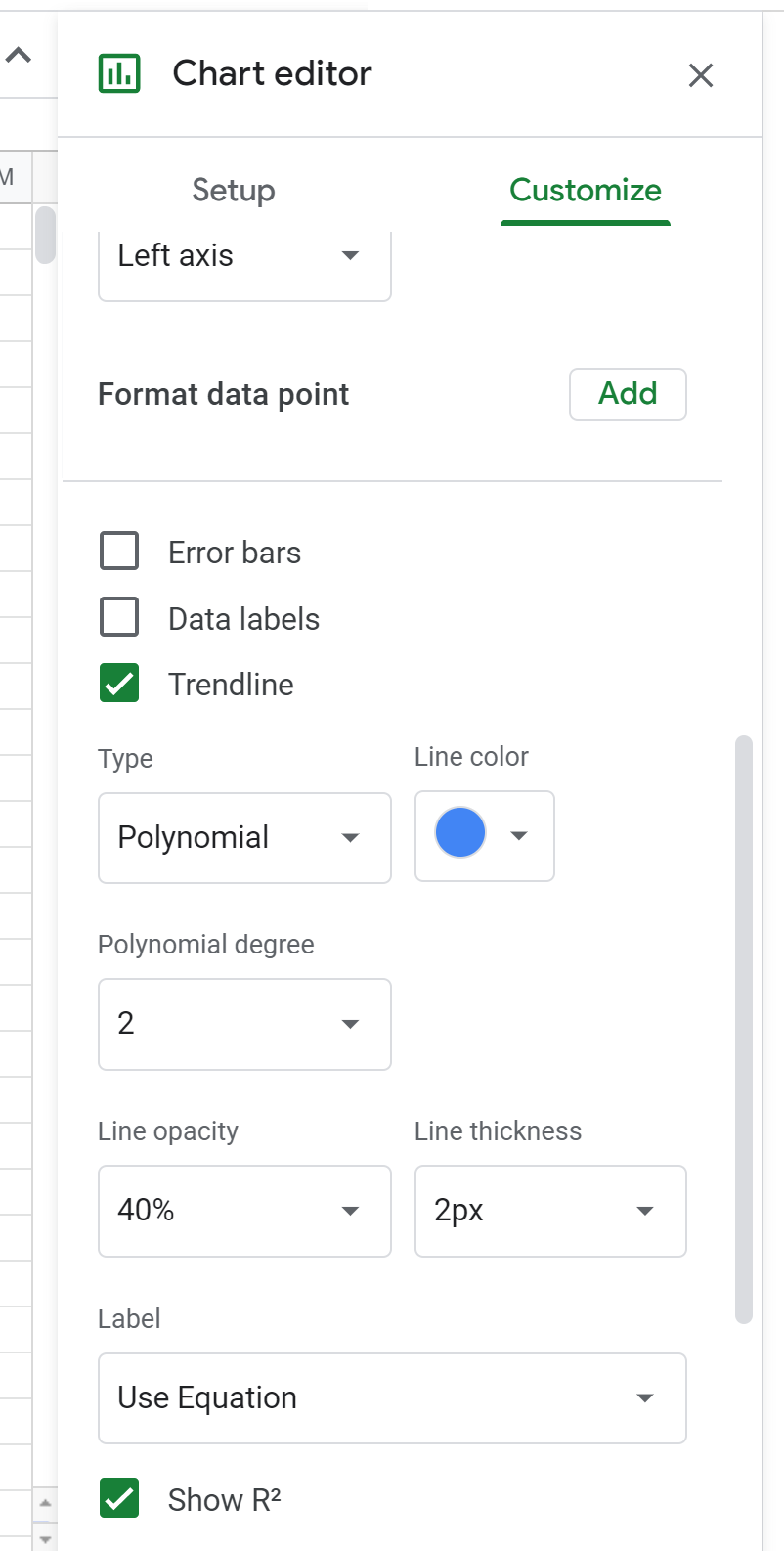
Далі натисніть «Серія» . Далі прокрутіть униз і встановіть прапорець поруч із Лінія тренду та змініть Тип на Поліноміальний . Для «Мітки» виберіть «Використовувати рівняння» , а потім поставте прапорець «Показати ^R2» .

Це призведе до появи такої формули над діаграмою розсіювання:

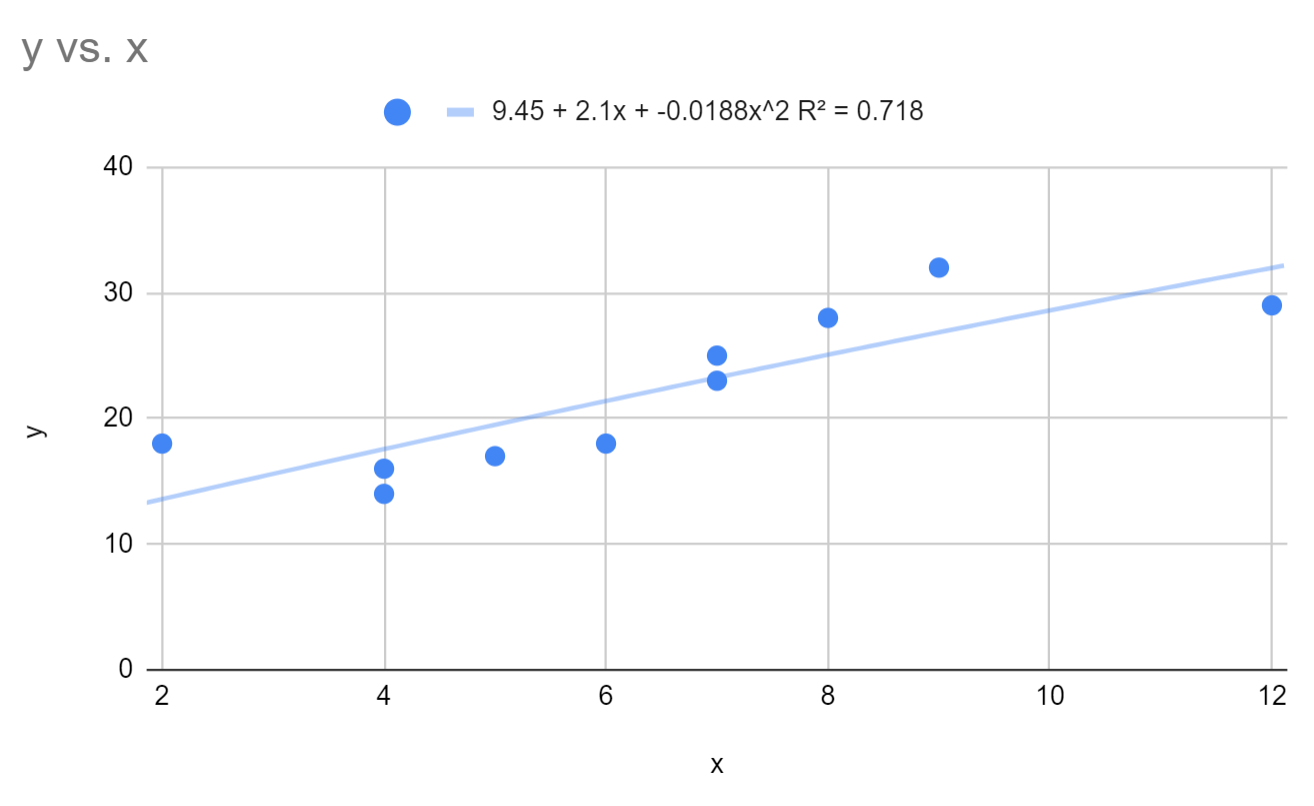
Ми бачимо, що підігнане рівняння поліноміальної регресії таке:

y = 9,45 + 2,1x – 0,0188x ²

R-квадрат для цієї моделі становить 0,718 .

Пам’ятайте, що R у квадраті показує нам відсоток варіації змінної відповіді, який можна пояснити змінними предиктора. Чим вище значення, тим краща модель.

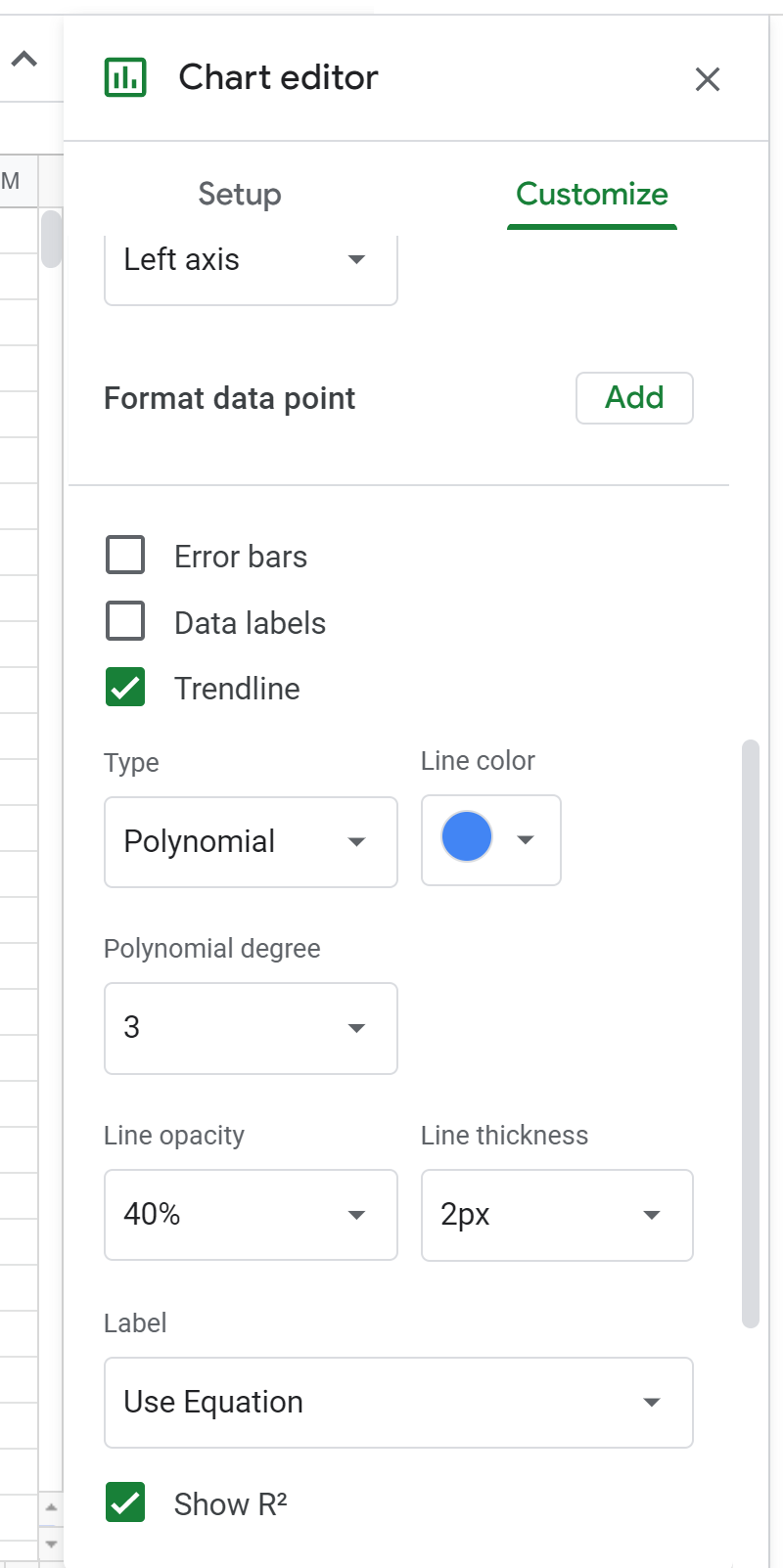
Далі змініть ступінь полінома на 3 у редакторі графіків:

Це призведе до появи такої формули над діаграмою розсіювання:

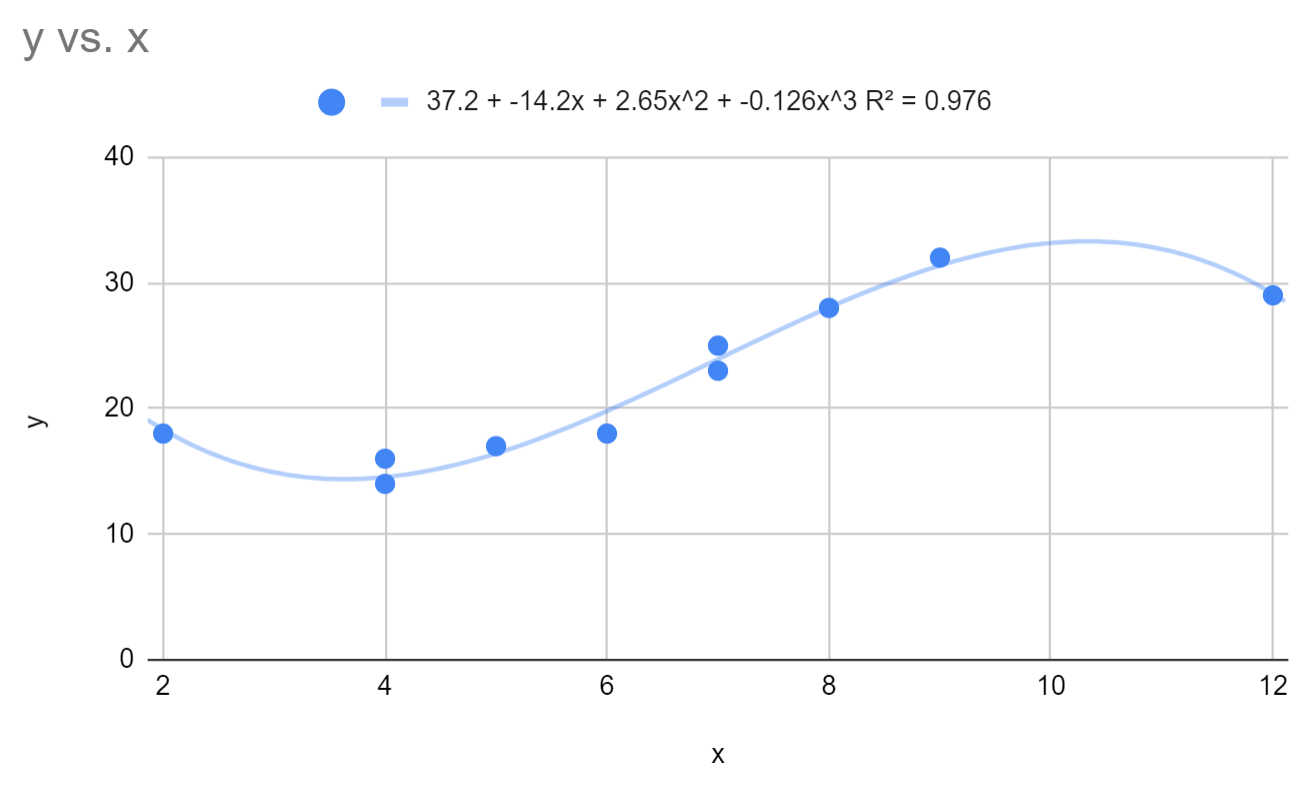
Це змінює підігнане рівняння поліноміальної регресії на:

y = 37,2 – 14,2x + 2,64x ² – 0,126x ³

R-квадрат для цієї моделі становить 0,976 .

Зауважте, що R-квадрат цієї моделі значно вищий, ніж у моделі поліноміальної регресії зі ступенем 2. Це означає, що ця модель регресії значно краще фіксує тенденцію базових даних.

Якщо ви зміните ступінь полінома на 4, R у квадраті ледве збільшиться до 0,981 . Це свідчить про те, що модель поліноміальної регресії 3-го ступеня є достатньою, щоб охопити тенденцію в цих даних.

Ми можемо використати підігнане рівняння регресії, щоб знайти очікуване значення змінної відповіді за даного значення змінної предиктора. Наприклад, якщо x = 4, тоді очікуване значення для y буде таким:

y = 37,2 – 14,2(4) + 2,64(4) ² – 0,126(4) ³ = 14,576

Ви можете знайти інші навчальні посібники Google Таблиць на цій сторінці .