Поліноміальна регресія в r (крок за кроком)

Поліноміальна регресія — це техніка, яку ми можемо використовувати, коли зв’язок між змінною предиктором і змінною відповіді нелінійний.

Цей тип регресії має вигляд:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

де h – «ступінь» полінома.

Цей підручник надає покроковий приклад виконання поліноміальної регресії в R.

Крок 1: Створіть дані

Для цього прикладу ми створимо набір даних, що містить кількість вивчених годин і підсумкову оцінку іспиту для класу з 50 студентів:

 #make this example reproducible
set.seed(1)

#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(data)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Крок 2: Візуалізуйте дані

Перш ніж пристосувати регресійну модель до даних, давайте спочатку створимо діаграму розсіювання, щоб візуалізувати зв’язок між годинами навчання та результатом іспиту:

 library (ggplot2)

ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

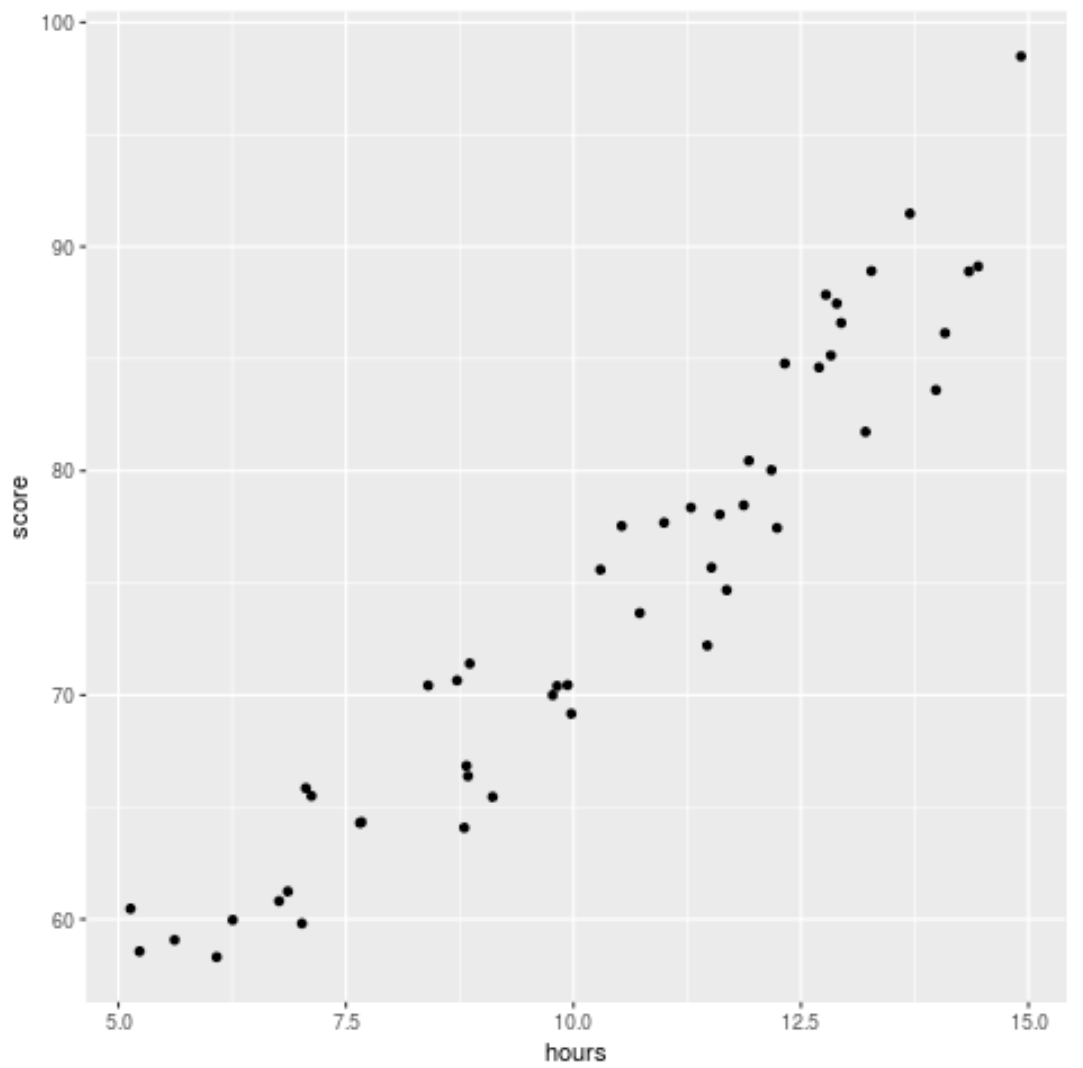
Ми бачимо, що дані мають дещо квадратичне співвідношення, що вказує на те, що поліноміальна регресія може краще відповідати даним, ніж проста лінійна регресія.

Крок 3: Підберіть моделі поліноміальної регресії

Далі ми підберемо п’ять різних моделей поліноміальної регресії зі ступенями h = 1…5 і використаємо k-кратну перехресну перевірку з k = 10 разів, щоб обчислити тест MSE для кожної моделі:

 #randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]

#define number of folds to use for k-fold cross-validation
K <- 10 

#define degree of polynomials to fit
degree <- 5

#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )

#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)

#Perform K-fold cross validation
for (i in 1:K){
    
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
    testData <- df.shuffled[testIndexes, ]
    trainData <- df.shuffled[-testIndexes, ]
    
#use k-fold cv to evaluate models
for (j in 1:degree){
        fit.train = lm (score ~ poly (hours,d), data=trainData)
        fit.test = predict (fit.train, newdata=testData)
        mse[i,j] = mean ((fit.test-testData$score)^2) 
    }
}

#find MSE for each degree 
colMeans(mse)

[1] 9.802397 8.748666 9.601865 10.592569 13.545547

З результату ми можемо побачити тест MSE для кожної моделі:

• Тест MSE зі ступенем h = 1: 9,80
• Тест MSE зі ступенем h = 2: 8,75
• Тест MSE зі ступенем h = 3: 9,60
• Тест MSE зі ступенем h = 4: 10,59
• Тест MSE зі ступенем h = 5: 13,55

Модель з найменшим критерієм MSE виявилася поліноміальною регресійною моделлю зі ступенем h = 2.

Це відповідає нашій інтуїції з початкової діаграми розсіювання: модель квадратичної регресії найкраще відповідає даним.

Крок 4: Проаналізуйте остаточну модель

Нарешті, ми можемо отримати коефіцієнти найкращої моделі:

 #fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)

#view summary of best model
summary(best)

Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-5.6589 -2.0770 -0.4599 2.5923 4.5122 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) 54.00526 5.52855 9.768 6.78e-13 ***
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569    
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

З результату ми бачимо, що остаточно встановлена модель:

Оцінка = 54,00526 – 0,07904*(годин) + 0,18596*(годин) ²

Ми можемо використовувати це рівняння, щоб оцінити бал, який отримає студент на основі кількості вивчених годин.

Наприклад, студент, який навчається 10 годин, повинен отримати оцінку 71,81 :

Оцінка = 54,00526 – 0,07904*(10) + 0,18596*(10) ² = 71,81

Ми також можемо побудувати підігнану модель, щоб побачити, наскільки добре вона відповідає необробленим даним:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

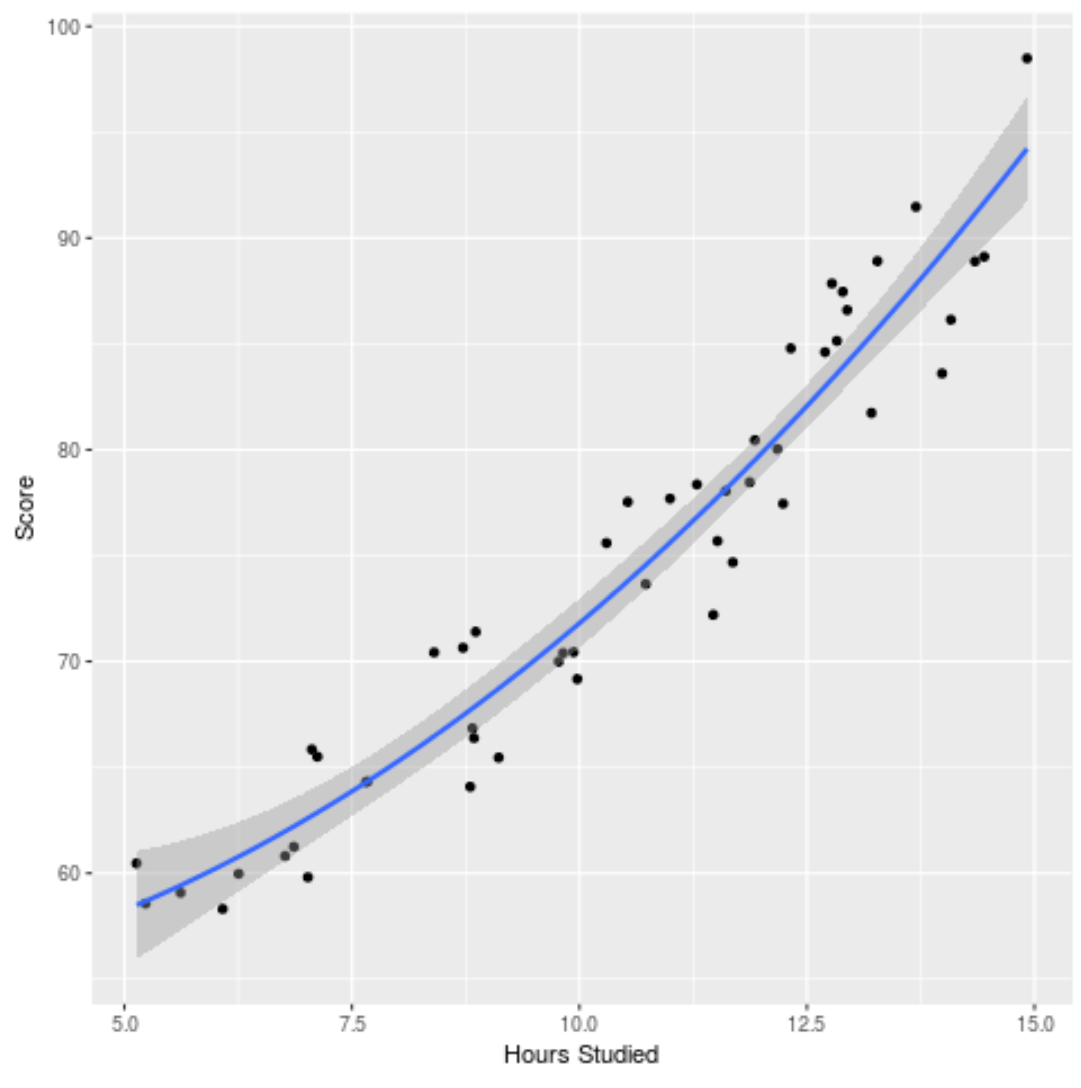
Ви можете знайти повний код R, використаний у цьому прикладі , тут .