Порівняння z балів різних розподілів

Z-показник показує, на скільки стандартних відхилень окреме значення даних падає від середнього. Він розраховується таким чином:

z-оцінка = (x – μ) / σ

золото:

• x: індивідуальне значення даних
• μ: середня популяція
• σ: стандартне відхилення сукупності

Z-показник для окремого значення можна інтерпретувати таким чином:

• Позитивний z-показник: індивідуальне значення вище середнього.
• Негативний z-показник: індивідуальне значення нижче середнього.
• Z-оцінка 0: індивідуальне значення дорівнює середньому.

Z-оцінки особливо корисні, коли ми хочемо порівняти відносне положення двох точок даних із двох різних розподілів. Щоб проілюструвати це, розглянемо наступний приклад.

Приклад: порівняння Z-оцінок

Оцінки за певний іспит до коледжу зазвичай розподіляються із середнім μ = 80 і стандартним відхиленням σ = 4. Дуейн отримує 84 бали за цей іспит.

Оцінки іншого іспиту в коледжі зазвичай розподіляються із середнім значенням μ = 85 і стандартним відхиленням σ = 8. Деббі отримує 90 на цьому іспиті.

Порівняно з власним розподілом іспитових балів, хто досяг найкращих результатів на іспиті?

Щоб відповісти на це запитання, ми можемо обчислити z-оцінку кожного іспиту:

Z-оцінка Дуейна = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1

Z-показник Деббі = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0,625

Хоча Деббі отримала вищу оцінку, оцінка Дуейна насправді вища порівняно з розподілом його конкретного іспиту.

Щоб зрозуміти це, допомагає візуалізація ситуації. Ось оцінка Дуейна в порівнянні з його конкретним іспитом:

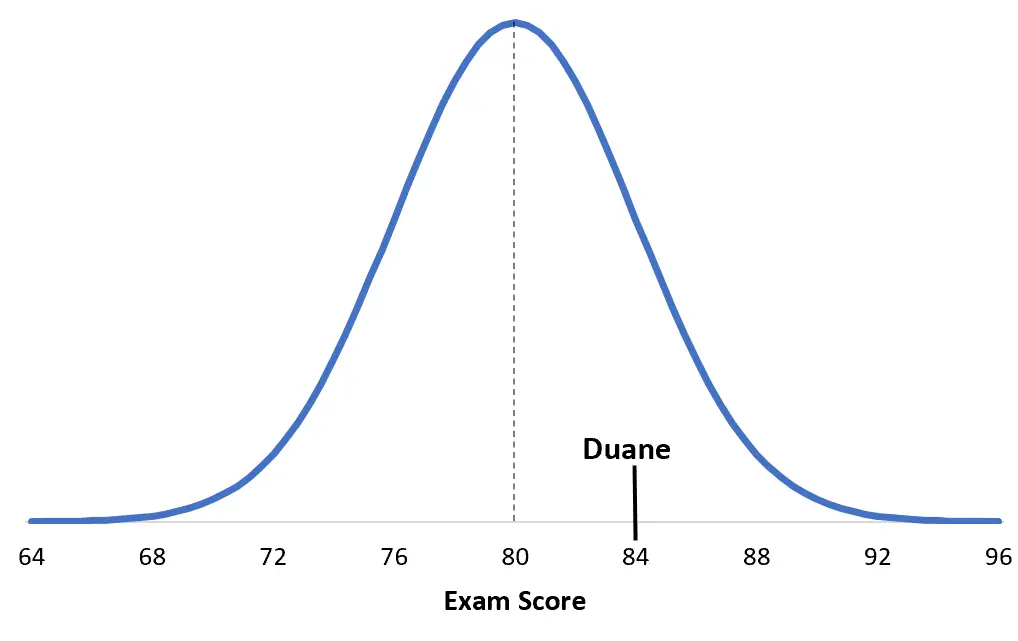
А ось оцінка Деббі з розбивки іспиту:

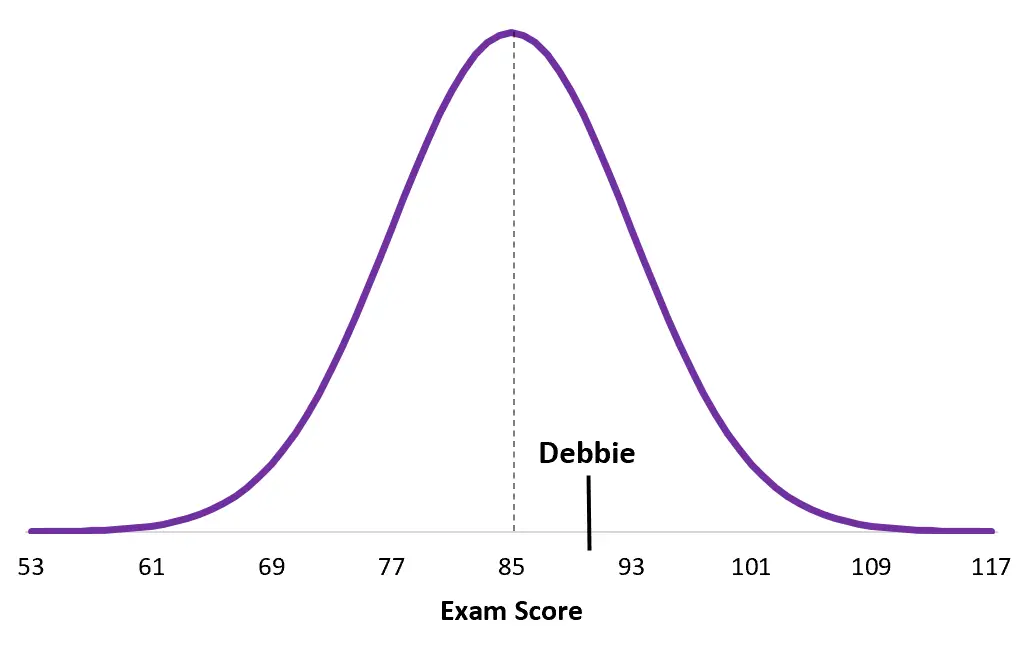
Зверніть увагу, наскільки показник Деббі ближчий до середнього показника населення, ніж показник Дуейна. Хоча вона має вищий загальний бал, її Z-бал нижчий просто тому, що середній бал на її конкретному іспиті вищий.

Цей приклад ілюструє, чому z-показники такі корисні для порівняння значень даних з різних розподілів: z-показники враховують середнє значення та стандартні відхилення розподілів, що дозволяє нам порівнювати значення даних з різних розподілів і бачити, які є вище порівняно з їхніми власними розподілами.

Додаткові ресурси

Калькулятор балів Z
Порівняйте калькулятор балів Z