Проста випадкова вибірка

за Редакція 6 Серпня, 2023 Статистика 0 коментарів

У цій статті ви дізнаєтесь, що таке проста випадкова вибірка та які існують типи простих випадкових вибірок. Крім того, на прикладі ми пояснюємо, як виконується проста випадкова вибірка. Нарешті ви зможете побачити переваги та недоліки простої випадкової вибірки.

Що таке проста випадкова вибірка?

У статистиці проста випадкова вибірка — це ймовірнісний метод, який використовується для відбору вибірки для дослідження. Основною характеристикою простої випадкової вибірки є те, що вона дає кожному елементу статистичної сукупності однакову ймовірність бути включеним до досліджуваної вибірки.

У простій випадковій вибірці елементи вибірки вибираються випадковим чином, тому отримана вибірка є повністю випадковою.

Тому, використовуючи просту випадкову вибірку, ймовірність отримання даної вибірки дорівнює ймовірності отримання будь-якої іншої вибірки. Нижче ми побачимо, як розраховується ця ймовірність.

Майте на увазі, що існують інші способи відбору осіб із вибірки. Найбільш використовувані типи вибірки в основному:

Проста випадкова вибірка
Стратифікована вибірка
Систематичний відбір проб
Кластерна вибірка

Концепція простої випадкової вибірки, безумовно, є найлегшою для розуміння, але іноді вона виявляється найскладнішою для реалізації саме через її випадкову природу.

Як зробити просту випадкову вибірку

Кроки для виконання простої випадкової вибірки такі:

Складіть список із усіма елементами сукупності.
Присвойте порядковий номер (1, 2, 3,…, n) кожному елементу сукупності.
Встановіть бажаний розмір вибірки .
Використовуйте генератор випадкових чисел , щоб згенерувати стільки чисел, скільки вибере розмір вибірки.
Особи, призначені для згенерованих номерів, є тими, хто вибраний для участі у вибірці.

Для генерації випадкових чисел існує кілька методів, найбільш традиційними є метод лотереї та метод таблиці чисел:

Метод лотереї полягає в тому, що всі числа складаються в коробку, перемішуються, а потім випадково витягуються.
Метод числової таблиці передбачає випадковий вибір чисел із таблиці, що містить усі можливі числа.

Хоча ви також можете використовувати будь-який із попередніх двох методів, вони потребують більше часу та краще підходять для менших розмірів вибірки. Зараз для швидшого генерування випадкових чисел використовуються комп’ютерні програми , наприклад, можна скористатися програмою Excel.

З іншого боку, ви повинні взяти до уваги, що розмір вибірки повинен бути адекватним, щоб мати мінімальну можливу помилку вибірки. Пошук ідеального розміру вибірки не є тривіальним; Якщо у вас є сумніви щодо цього, ви можете пошукати на нашому веб-сайті статтю, у якій ми пояснюємо, як це зробити.

Простий приклад випадкової вибірки

Коли ми побачимо визначення простої випадкової вибірки, ми побачимо розв’язаний приклад того, як виконується цей тип вибірки.

Наприклад, якщо в компанії 2000 працівників, і ми хочемо провести статистичне дослідження з вибіркою з 400 працівників, щоб вибрати осіб, які будуть частиною вибірки за допомогою простої випадкової вибірки, перше, що потрібно зробити, складається з присвоєння кожному працівнику номера від 1 до 2000.

Після того, як номери призначені, нам потрібно навмання вибрати 400 чисел. У цьому випадку обсяг вибірки досить великий, тому найкраще використовувати комп’ютерну програму, наприклад Excel.

Тоді 400 працівників, відібраних для участі в дослідженні, будуть тими, чия кількість була визначена на попередньому кроці.

У цьому прикладі 400 елементів вважалися достатньо репрезентативним розміром вибірки, але логічно ця кількість змінюватиметься залежно від експерименту.

Типи простої випадкової вибірки

Існує два типи простої випадкової вибірки:

Проста випадкова вибірка із заміною : вибраний елемент кадру вибірки повертається та може бути обраний знову.
Проста випадкова вибірка без заміни : елемент, вибраний як частина вибірки, видаляється і більше не може бути обраний.

Проста випадкова вибірка із заміною є найпростішим типом вибірки, оскільки завжди повторюється той самий процес, щоб вибрати елемент із вибірки. Однак проста випадкова вибірка без заміни використовується більш широко, оскільки вона точніша. Обидва типи пояснюються більш детально нижче.

Проста випадкова вибірка з заміною

Проста випадкова вибірка із заміною передбачає повернення кожного вибраного елемента до системи вибірки, щоб існувала можливість вибрати його знову.

Таким чином, можна отримати зразок з одного елемента, обраного кілька разів, хоча це, очевидно, дуже малоймовірно.

Математично це дуже простий тип вибірки, оскільки ймовірності кожного вилучення однакові. Тому зазвичай починають вивчати цю методику відбору проб раніше за інших.

У простій випадковій вибірці з заміною ймовірність отримання вибірки певного порядку можна розрахувати за такою формулою:

$P=\cfrac{1}{N^n}$

бути

$N$

загальна кількість елементів сукупності і

$n$

кількість незалежних вилучень, які будуть виконані.

З іншого боку, коли порядок не має значення, ймовірність отримання зразка обчислюється за таким виразом:

$P=\cfrac{n!}{\displaystyle N^n\prod_{i=1}^z k_i!}$

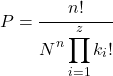
золото

$n$

– кількість незалежних вилучень,

$z$

кількість різних елементів у вибірці і

$k_i$

скільки разів ви хочете, щоб елемент з’явився

$i$

у зразку.

Нарешті, знайти ймовірність включення елемента

$i$

, тобто ймовірність включення елемента

$i$

У прикладі слід використовувати таку формулу:

$\displaystyle \pi_i=1-\left(1-\frac{1}{N}\right)^n$

Проста випадкова вибірка без заміни

Проста випадкова вибірка без заміни передбачає відбір із вибірки стільки індивідів, скільки вказує бажаний розмір вибірки, щоб кожну індивідуум не можна було вибрати повторно після відбору. Таким чином, кожен вибраний елемент видаляється, а не замінюється.

Коли ми говоримо про просту випадкову вибірку, ми зазвичай маємо на увазі вибірку, у якій особи не замінюються, оскільки вона найчастіше використовується на практиці.

Для визначення ймовірності отримання вибірки з певним порядком при простій випадковій вибірці з заміною використовується наступна формула:

$P=\cfrac{1}{n!\begin{pmatrix}N\\n\end{pmatrix}}$

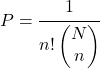
бути

$N$

загальна кількість елементів у популяції і

$n$

кількість залежних вилучень для виконання.

З іншого боку, якщо порядок екстракції не потрібно брати до уваги, ймовірність отримання зразка дорівнює:

$P=\cfrac{1}{\begin{pmatrix}N\\n\end{pmatrix}}$

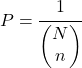
Нарешті, ймовірність включення елемента в просту випадкову вибірку без заміни обчислюється за допомогою правила Лапласа:

$\displaystyle \pi_i=\frac{n}{N}$

Переваги та недоліки простої випадкової вибірки

Проста випадкова вибірка має такі переваги та недоліки:

перевага	Недоліки
Легко зрозуміти.	Необхідний перелік усіх елементів популяції.
Усі можливі вибірки є рівноімовірними.	Це може бути дуже дорогим для великих розмірів вибірки.
Зазвичай отримують репрезентативні зразки.	Він, як правило, має більші помилки вибірки.
Для відбору зразків не потрібні технічні знання.	Знання, які дослідник може мати в досліджуваній області, не використовуються.
Дозволяє швидко розрахувати середні значення та відхилення.	Вибірка може бути нерепрезентативною, якщо вона занадто мала.
Існує статистичне програмне забезпечення для аналізу даних.	Не підходить для досліджень, які потребують індивідуальних співбесід.

Як ми бачили, однією з основних характеристик простої випадкової вибірки є те, що її легко зрозуміти та пояснити. Дійсно, особа, яка проводить відбір проб, не повинна бути експертом у галузі аналізу. Однак це як сильна, так і слабка сторона, оскільки в інших типах вибірки знання аналітика можна використовувати для досягнення кращої вибірки.

Так само, оскільки вибірка є випадковою, ймовірність того, що той чи інший елемент стане досліджуваною вибіркою, є рівноімовірною, на відміну від інших типів вибірки.

Хоча зазвичай отримують репрезентативні вибірки генеральної сукупності, помилка вибірки при простій випадковій вибірці велика порівняно з іншими типами вибірки. Крім того, вибірка може навіть не бути репрезентативною, якщо розмір особин невеликий.

Дуже привабливою властивістю простої випадкової вибірки є те, що її можна проводити за допомогою комп’ютерних програм, що дозволяє швидко проводити статистичні розрахунки.

Нарешті, слід зазначити, що проста випадкова вибірка може бути дорожчою, ніж інші типи вибірки, особливо в широко розсіяних популяціях, оскільки може вимагати використання більших ресурсів для дослідження. Наприклад, оскільки це випадкова вибірка, люди, відібрані для проведення дослідження, можуть бути географічно розосереджені, і, отже, проведення особистих інтерв’ю буде набагато дорожчим.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше