Проста лінійна регресія
У цій статті пояснюється, що таке проста лінійна регресія в статистиці та як вона виконується. Подібним чином ви знайдете розв’язану просту вправу лінійної регресії та, крім того, простий калькулятор лінійної регресії в Інтернеті.
Що таке проста лінійна регресія?
Проста лінійна регресія — це статистична модель, яка використовується для зв’язку незалежної змінної, і ми намагаємося наближено визначити зв’язок між двома змінними.
Тому проста лінійна регресія використовується для знаходження рівняння, яке лінійно зв’язує дві змінні. За логікою зв’язок між двома змінними має бути лінійним, інакше слід використовувати інший тип регресійної моделі.
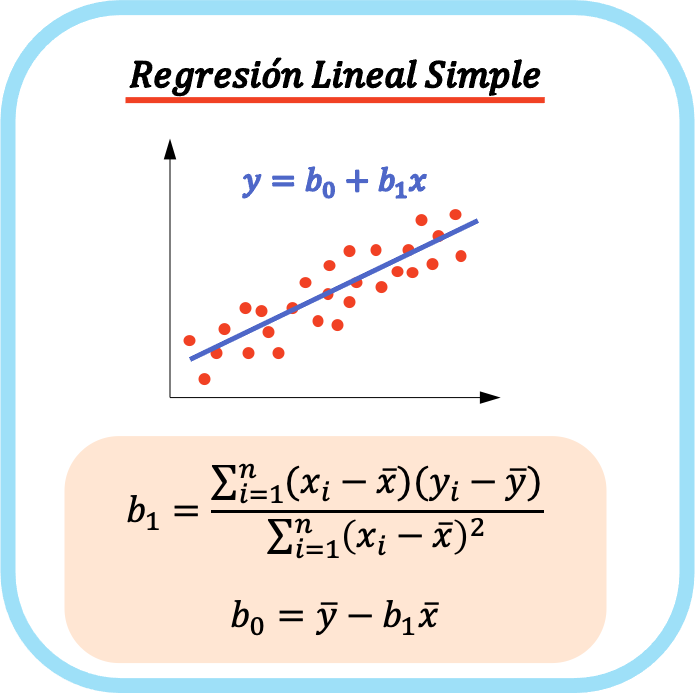
Рівняння простої моделі лінійної регресії складається з двох коефіцієнтів: константи рівняння (b 0 ) і коефіцієнта кореляції між двома змінними (b 1 ). Отже, рівняння для простої моделі лінійної регресії має вигляд y=b 0 +b 1 x.
![]()
Рівняння для простої лінійної регресії зображено у вигляді прямої лінії, тому коефіцієнт b 0 є точкою перетину, а коефіцієнт b 1 — кутом нахилу прямої.
Прості формули лінійної регресії
Формули для розрахунку коефіцієнтів простої лінійної регресії такі:
👉 Ви можете використовувати калькулятор нижче, щоб обчислити коефіцієнти простої лінійної регресії для будь-якого набору даних.
Очевидно, що рівняння, отримане в результаті моделі простої лінійної регресії, не зможе вгадати точне значення всіх спостережень, оскільки ця модель просто намагається знайти рівняння, яке наближено відображає зв’язок між двома змінними. Таким чином, залишок визначається як різниця між справжнім значенням і значенням, оціненим за моделлю лінійної регресії.
![]()
Зауважте, що метою моделі простої лінійної регресії є мінімізація квадратів залишків, тобто проста лінійна регресія базується на критерії найменших квадратів .
Конкретний приклад простої лінійної регресії
Щоб завершити розуміння методу простої лінійної регресії, ось практичний покроковий приклад, у якому рівняння моделі простої лінійної регресії обчислюється на основі набору статистичних даних.
- Після іспиту зі статистики п’ятьох студентів запитали, скільки годин навчання вони присвятили іспиту. Дані представлені в таблиці нижче. Виконайте просту модель лінійної регресії зібраних статистичних даних, щоб лінійно зв’язати навчальні години з отриманою оцінкою.

Щоб виконати просту модель лінійної регресії, ми повинні визначити коефіцієнти b 0 і b 1 рівняння, і для цього ми повинні використовувати формули, наведені в розділі вище.
Однак, щоб застосувати прості формули лінійної регресії, ми повинні спочатку обчислити середнє значення незалежної змінної та середнє значення залежної змінної:
![Rendered by QuickLaTeX.com \begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7a7aa6f1f20fa4ff0d61a2ad0dd2ea1f_l3.png)
Тепер, коли ми знаємо середні значення змінних, ми обчислюємо коефіцієнт b 1 моделі за допомогою відповідної формули:
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c9d90c766487cd7b6924e6b23d2d9c78_l3.png)
Нарешті, ми розраховуємо коефіцієнт b 0 моделі за її відповідною формулою:
![Rendered by QuickLaTeX.com \begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c72e6b89a75681a88cf751ca39079240_l3.png)
Коротше кажучи, рівняння для моделі простої лінійної регресії проблеми таке:
![]()
Нижче ви можете побачити графічне представлення вибіркових даних, а також пряму лінію моделі простої лінійної регресії:

Нарешті, коли ми розрахували рівняння моделі простої лінійної регресії, залишається лише інтерпретувати отриманий результат. Для цього необхідно розрахувати коефіцієнт детермінації регресійної моделі, ви можете побачити, як це робиться, пошукавши відповідну статтю на нашому сайті.
Прості припущення лінійної регресії
Щоб виконати просту лінійну регресію, мають бути виконані такі припущення:
- Незалежність : досліджувані залишки повинні бути незалежними один від одного. Поширеним способом забезпечення незалежності моделі є додавання до процесу вибірки випадковості.
- Гомоскедастичність : дисперсії залишків повинні бути однорідними, тобто мінливість залишків має бути постійною.
- Нормальність : залишки мають бути нормально розподілені, або, іншими словами, вони повинні відповідати нормальному розподілу із середнім 0.
- Лінійність – зв’язок між незалежною змінною та залежною змінною має бути лінійним.
Простий калькулятор лінійної регресії
Підключіть зразки даних до калькулятора нижче, щоб узгодити просту модель лінійної регресії між двома змінними. Потрібно розділити пари даних так, щоб у першому полі були лише значення незалежної змінної X, а в другому – лише значення залежної змінної Y.
Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.
Проста і множинна лінійна регресія
Нарешті, ми побачимо, яка різниця між простою лінійною регресією та множинною лінійною регресією, оскільки це два типи лінійних регресій, які часто використовуються в статистиці.
Множинна лінійна регресія дає змогу математично пов’язати дві або більше пояснювальних змінних зі змінною відповіді. Тобто при множинній лінійній регресії створюється модель, в якій є принаймні дві незалежні змінні.
Отже, різниця між простою лінійною регресією та множинною лінійною регресією полягає в кількості незалежних змінних. У простій лінійній регресії існує лише одна незалежна змінна, тоді як у множинній лінійній регресії є дві або більше незалежних змінних.