Як виконати просту лінійну регресію в excel

Проста лінійна регресія — це метод, який ми можемо використовувати для розуміння зв’язку між пояснювальною змінною x і змінною відповіді y.

У цьому посібнику пояснюється, як виконати просту лінійну регресію в Excel.

Приклад: проста лінійна регресія в Excel

Припустімо, ми хочемо зрозуміти залежність між кількістю годин, які студент готує до іспиту, та оцінкою, яку він отримує на іспиті.

Щоб дослідити цей зв’язок, ми можемо виконати просту лінійну регресію, використовуючи вивчені години як пояснювальну змінну та результати іспитів як змінну відповіді.

Виконайте наведені нижче дії в Excel, щоб виконати просту лінійну регресію.

Крок 1: Введіть дані.

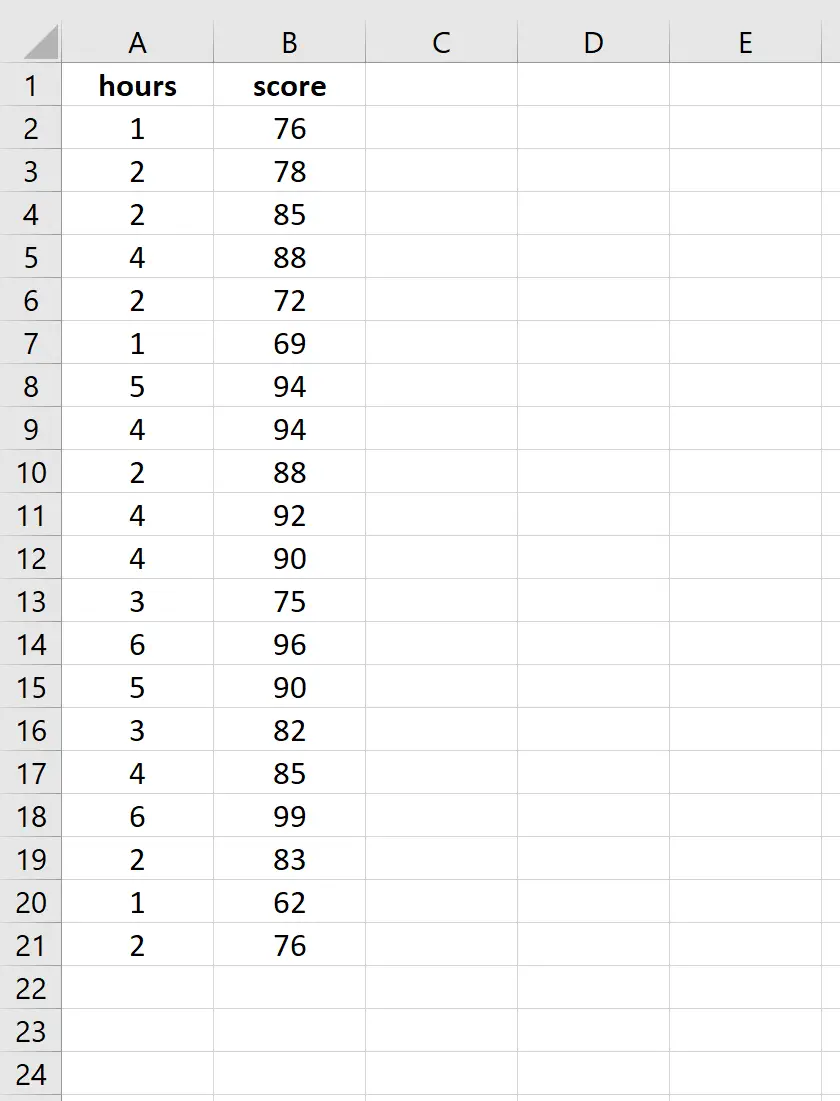
Введіть наступні дані щодо кількості вивчених годин та отриманих іспитів для 20 студентів:

Крок 2: Візуалізуйте дані.

Перш ніж виконувати просту лінійну регресію, корисно створити діаграму розсіювання даних, щоб переконатися, що між годинами навчання та результатом іспиту дійсно існує лінійна залежність.

Виділіть дані в стовпцях A і B. У верхній стрічці Excel перейдіть до вкладки «Вставлення» . У групі «Графіка» клацніть «Вставити точкову лінію» (X, Y) і клацніть перший параметр із позначкою «Точкова точка» . Це автоматично створить таку хмару точок:

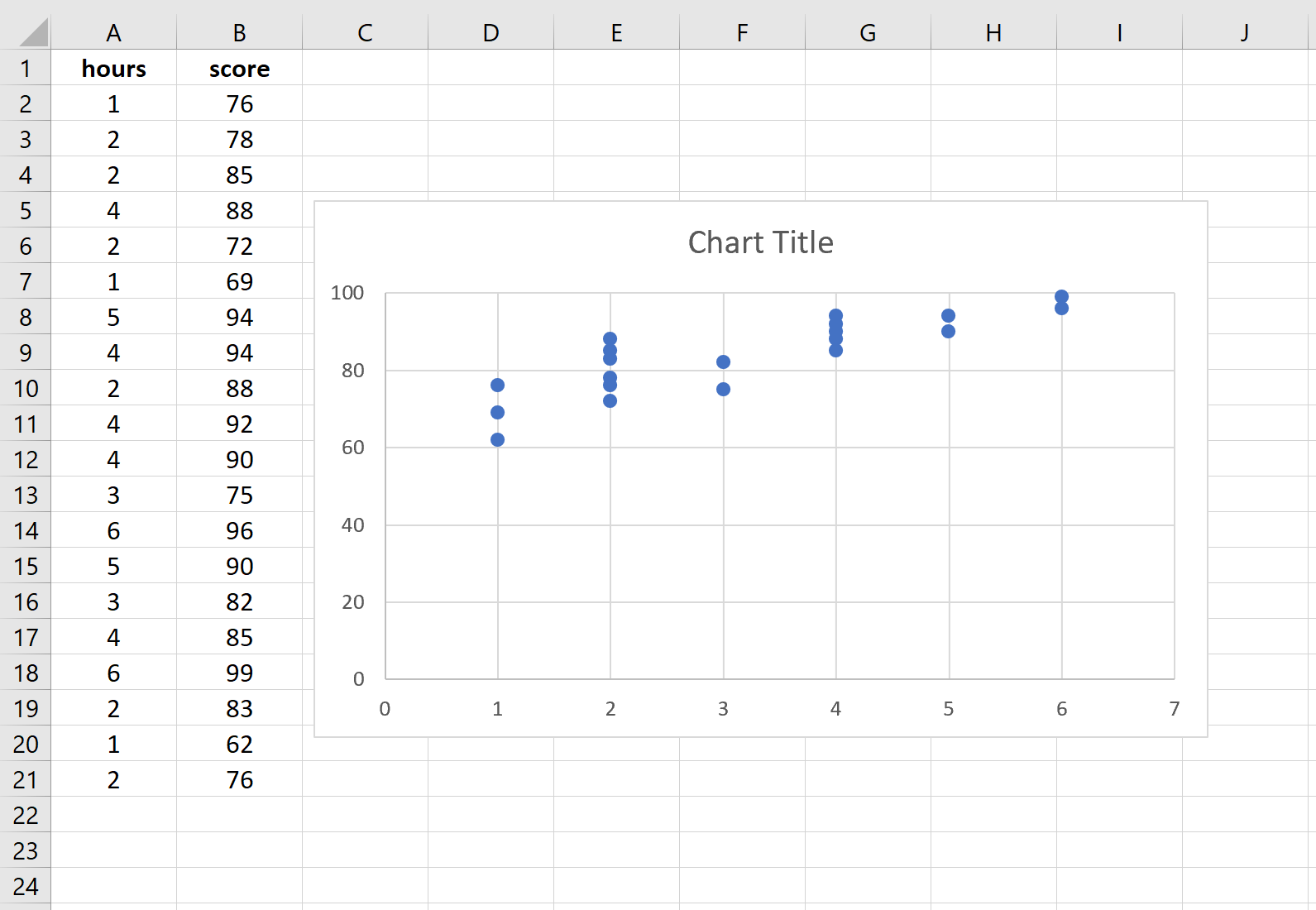
Кількість вивчених годин відображається на осі абсцис, а результати іспитів – на осі у. Ми бачимо, що існує лінійна залежність між двома змінними: більше годин навчання пов’язане з вищими оцінками за іспит.

Щоб кількісно визначити зв’язок між цими двома змінними, ми можемо виконати просту лінійну регресію.

Крок 3. Виконайте просту лінійну регресію.

На верхній стрічці Excel перейдіть на вкладку «Дані» та натисніть «Аналіз даних» . Якщо ви не бачите цей параметр, спершу потрібно інсталювати безкоштовне програмне забезпечення Analysis ToolPak .

Коли ви натиснете «Аналіз даних», з’явиться нове вікно. Виберіть «Регресія» та натисніть «ОК».

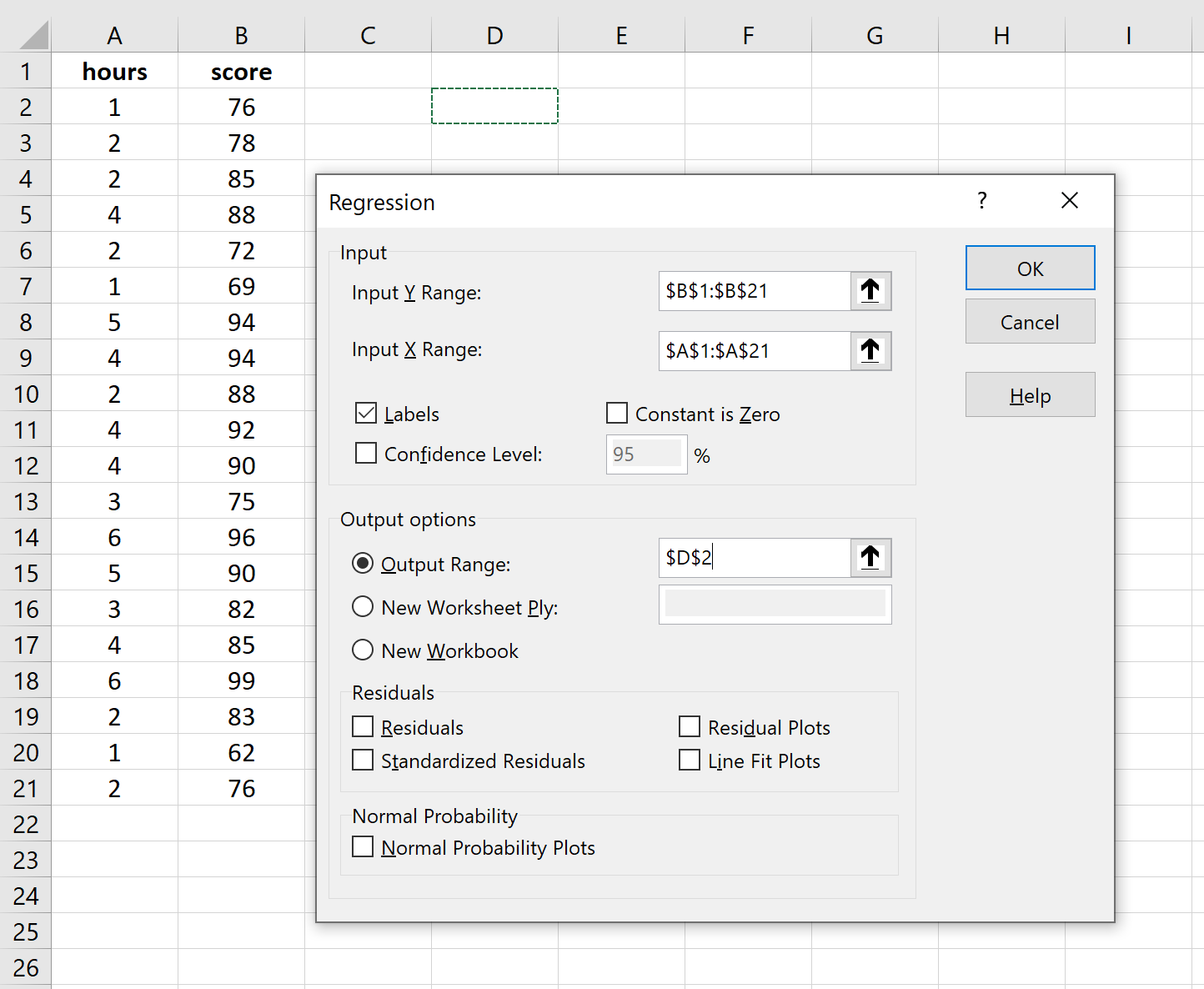
Для Input Y Range заповніть масив значень для змінної відповіді. Для Input X Range заповніть масив значень для пояснювальної змінної.

Поставте прапорець біля пункту «Мітки» , щоб повідомити Excel, що ми включили імена змінних у вхідні діапазони.

Для параметра «Діапазон результатів» виберіть комірку, у якій потрібно відобразити результат регресії.

Потім натисніть OK .

Автоматично з’явиться такий результат:

Крок 4: Інтерпретуйте результат.

Ось як інтерпретувати найбільш відповідні числа в результаті:

Квадрат R: 0,7273 . Це називається коефіцієнтом детермінації. Це частка дисперсії у змінній відповіді, яку можна пояснити пояснювальною змінною. У цьому прикладі 72,73% варіації оцінок на іспитах пояснюється кількістю вивчених годин.

Стандартна похибка: 5,2805 . Це середня відстань між спостережуваними значеннями та лінією регресії. У цьому прикладі спостережувані значення відхиляються в середньому на 5,2805 одиниць від лінії регресії.

F: 47,9952 . Це загальна F-статистика для регресійної моделі, розрахована як регресійна MS/залишкова MS.

Значення F: 0,0000 . Це p-значення, пов’язане із загальною статистикою F. Це говорить нам про те, чи є модель регресії статистично значущою чи ні. Іншими словами, це повідомляє нам, чи має пояснювальна змінна статистично значущий зв’язок зі змінною відповіді. У цьому випадку p-значення менше 0,05, що вказує на те, що існує статистично значущий зв’язок між вивченими годинами та оцінкою, отриманою на іспиті.

Коефіцієнти: Коефіцієнти дають нам числа, необхідні для написання розрахункового рівняння регресії. У цьому прикладі розраховане рівняння регресії таке:

оцінка за іспит = 67,16 + 5,2503*(години)

Ми інтерпретуємо коефіцієнт годин так, що за кожну додаткову вивчену годину оцінка іспиту має зрости в середньому на 5,2503 . Ми інтерпретуємо коефіцієнт перетину так, що очікуваний іспитовий бал для студента, який вивчає нуль годин, становить 67,16 .

Ми можемо використовувати це оцінене рівняння регресії, щоб обчислити очікуваний іспитовий бал для студента на основі кількості годин навчання.

Наприклад, студент, який навчається протягом трьох годин, повинен отримати іспитовий бал 82,91 :

іспитовий бал = 67,16 + 5,2503*(3) = 82,91

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в Excel:

Як створити діаграму залишку в Excel
Як побудувати інтервал прогнозу в Excel
Як створити діаграму QQ в Excel