Як виконати просту лінійну регресію в python (крок за кроком)
Проста лінійна регресія — це техніка, яку ми можемо використати, щоб зрозуміти зв’язок між окремою пояснювальною змінною та окремою змінною відповіді .
Ця техніка знаходить рядок, який найкраще «відповідає» даним і набуває такої форми:
ŷ = b 0 + b 1 x
золото:
- ŷ : оцінене значення відповіді
- b 0 : Початок лінії регресії
- b 1 : Нахил лінії регресії
Це рівняння може допомогти нам зрозуміти взаємозв’язок між пояснювальною змінною та змінною відповіді та (якщо воно є статистично значущим) його можна використовувати для прогнозування значення змінної відповіді, враховуючи значення пояснювальної змінної.
Цей підручник надає покрокове пояснення того, як виконувати просту лінійну регресію в Python.
Крок 1. Завантажте дані
Для цього прикладу ми створимо підроблений набір даних, що містить такі дві змінні для 15 студентів:
- Загальна кількість годин, відпрацьованих на окремі іспити
- Результат іспиту
Ми спробуємо підібрати просту модель лінійної регресії, використовуючи години як пояснювальну змінну та результати іспитів як змінну відповіді.
Наступний код показує, як створити цей фальшивий набір даних у Python:
import pandas as pd #create dataset df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14], ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]}) #view first six rows of dataset df[0:6] hours score 0 1 64 1 2 66 2 4 76 3 5 73 4 5 74 5 6 81
Крок 2: Візуалізуйте дані
Перш ніж підганяти просту модель лінійної регресії, ми повинні спочатку візуалізувати дані, щоб зрозуміти їх.
По-перше, ми хочемо переконатися, що зв’язок між годинами та оцінкою є приблизно лінійним, оскільки це припущення, що лежить в основі простої лінійної регресії.
Ми можемо створити просту діаграму розсіювання, щоб візуалізувати зв’язок між двома змінними:
import matplotlib.pyplot as plt plt. scatter (df.hours, df.score) plt. title (' Hours studied vs. Exam Score ') plt. xlabel (' Hours ') plt. ylabel (' Score ') plt. show ()
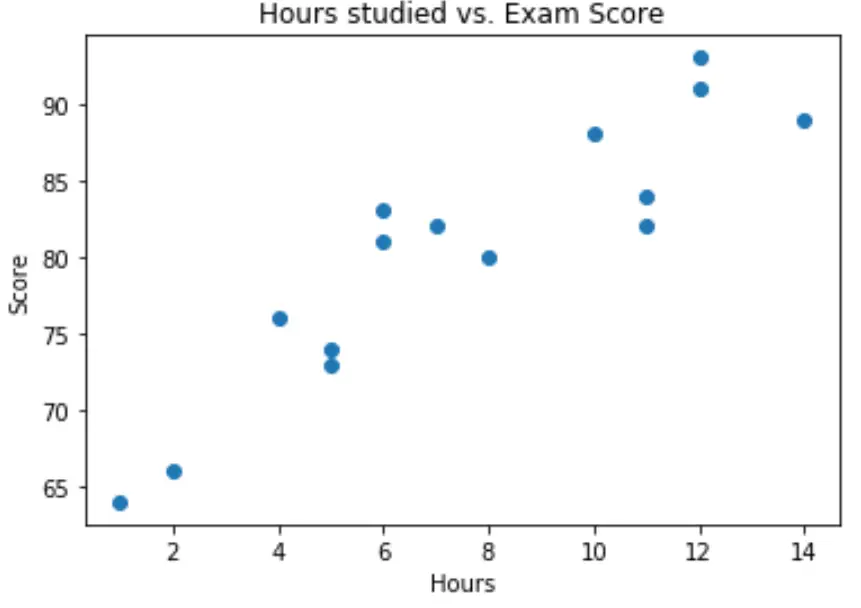
З графіка ми бачимо, що залежність виглядає лінійною. Зі збільшенням кількості годин оцінка також має тенденцію до лінійного зростання.
Тоді ми можемо створити коробкову діаграму для візуалізації розподілу результатів іспиту та перевірки викидів . За замовчуванням Python визначає спостереження як викид, якщо воно в 1,5 рази перевищує інтерквартильний діапазон вище третього квартиля (Q3) або в 1,5 рази перевищує інтерквартильний діапазон нижче першого квартиля (Q1).
Якщо спостереження виходить за межі, на прямокутній діаграмі з’явиться маленьке коло:
df. boxplot (column=[' score '])
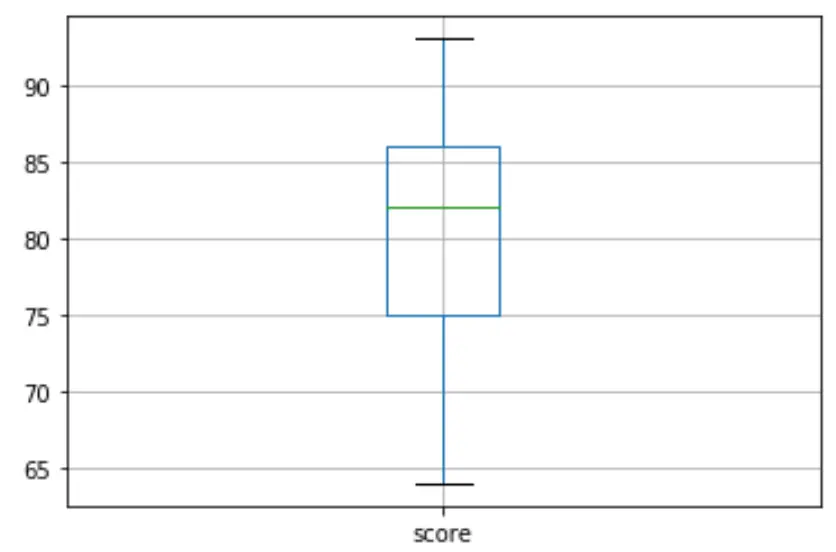
На прямокутній діаграмі немає маленьких кружечків, а це означає, що в нашому наборі даних немає викидів.
Крок 3: Виконайте просту лінійну регресію
Після того, як ми підтвердили, що зв’язок між нашими змінними є лінійним і немає викидів, ми можемо перейти до підгонки простої моделі лінійної регресії, використовуючи години як пояснювальну змінну та бал як змінну відповіді:
Примітка: ми будемо використовувати функцію OLS() з бібліотеки statsmodels, щоб відповідати регресійній моделі.
import statsmodels.api as sm #define response variable y = df[' score '] #define explanatory variable x = df[[' hours ']] #add constant to predictor variables x = sm. add_constant (x) #fit linear regression model model = sm. OLS (y,x). fit () #view model summary print ( model.summary ()) OLS Regression Results ==================================================== ============================ Dept. Variable: R-squared score: 0.831 Model: OLS Adj. R-squared: 0.818 Method: Least Squares F-statistic: 63.91 Date: Mon, 26 Oct 2020 Prob (F-statistic): 2.25e-06 Time: 15:51:45 Log-Likelihood: -39,594 No. Observations: 15 AIC: 83.19 Df Residuals: 13 BIC: 84.60 Model: 1 Covariance Type: non-robust ==================================================== ============================ coef std err t P>|t| [0.025 0.975] -------------------------------------------------- ---------------------------- const 65.3340 2.106 31.023 0.000 60.784 69.884 hours 1.9824 0.248 7.995 0.000 1.447 2.518 ==================================================== ============================ Omnibus: 4,351 Durbin-Watson: 1,677 Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329 Skew: 0.092 Prob(JB): 0.515 Kurtosis: 1.554 Cond. No. 19.2 ==================================================== ============================
З підсумку моделі ми можемо побачити, що підігнане рівняння регресії таке:
Оцінка = 65,334 + 1,9824*(години)
Це означає, що кожна додаткова вивчена година пов’язана зі збільшенням середнього балу на іспиті на 1,9824 бали. А вихідне значення 65 334 говорить нам про середній очікуваний іспитовий бал для студента, який навчається нуль годин.
Ми також можемо використати це рівняння, щоб знайти очікуваний бал за іспит на основі кількості годин, які навчається студент. Наприклад, студент, який навчається протягом 10 годин, повинен отримати іспитовий бал 85,158 :
Оцінка = 65,334 + 1,9824*(10) = 85,158
Ось як інтерпретувати решту короткого опису моделі:
- P>|t| : це p-значення, пов’язане з коефіцієнтами моделі. Оскільки p-значення для годин (0,000) є значно меншим за 0,05, ми можемо сказати, що існує статистично значущий зв’язок між годинами та балом .
- R-квадрат: це число говорить нам про те, що відсоток варіації оцінок на іспитах можна пояснити кількістю вивчених годин. Загалом, чим більше значення R-квадрат регресійної моделі, тим краще пояснювальні змінні здатні передбачити значення змінної відповіді. У цьому випадку 83,1% варіації балів пояснюється вивченими годинами.
- F-статистика та p-значення: F-статистика ( 63.91 ) і відповідне p-значення ( 2.25e-06 ) повідомляють нам про загальну значущість регресійної моделі, тобто чи пояснювальні змінні в моделі корисні для пояснення варіації. . у змінній відповіді. Оскільки p-значення в цьому прикладі менше 0,05, наша модель є статистично значущою, і години вважаються корисними для пояснення варіації оцінки .
Крок 4: Створіть залишкові ділянки
Після підгонки моделі простої лінійної регресії до даних останнім кроком є створення графіків залишків.
Одне з ключових припущень лінійної регресії полягає в тому, що залишки регресійної моделі розподілені приблизно нормально і є гомоскедастичними на кожному рівні пояснювальної змінної. Якщо ці припущення не виконуються, результати нашої моделі регресії можуть бути оманливими або ненадійними.
Щоб переконатися, що ці припущення виконуються, ми можемо створити такі залишкові графіки:
Графік залишків проти підігнаних значень: цей графік корисний для підтвердження гомоскедастичності. На осі абсцис відображаються підібрані значення, а на осі у – залишки. Поки залишки виглядають випадково та рівномірно розподіленими по всьому графіку навколо нульового значення, ми можемо припустити, що гомоскедастичність не порушена:
#define figure size fig = plt. figure (figsize=(12.8)) #produce residual plots fig = sm.graphics. plot_regress_exog (model, ' hours ', fig=fig)
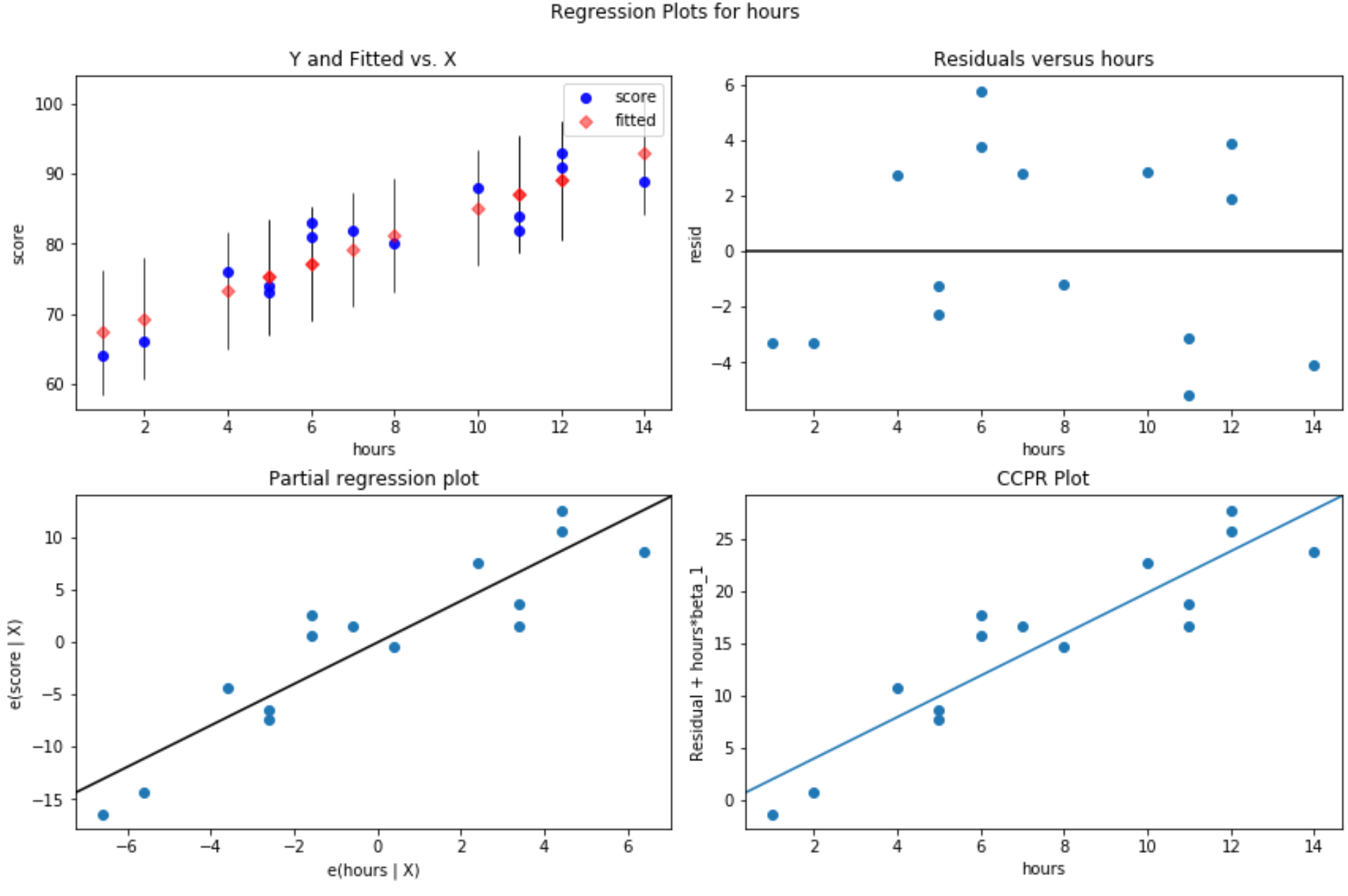
Виробляється чотири ділянки. У верхньому правому куті — це залишковий графік порівняно зі скоригованим графіком. Вісь абсцис на цьому графіку показує фактичні значення точок змінної предиктора, а вісь ординат показує залишкове значення для цього значення.
Оскільки залишки здаються випадковим чином розкиданими навколо нуля, це вказує на те, що гетероскедастичність не є проблемою для пояснювальної змінної.
Графік QQ: цей графік корисний для визначення того, чи відповідають залишки нормальному розподілу. Якщо значення даних на графіку йдуть по приблизно прямій лінії під кутом 45 градусів, то дані розподіляються нормально:
#define residuals res = model. reside #create QQ plot fig = sm. qqplot (res, fit= True , line=" 45 ") plt.show()
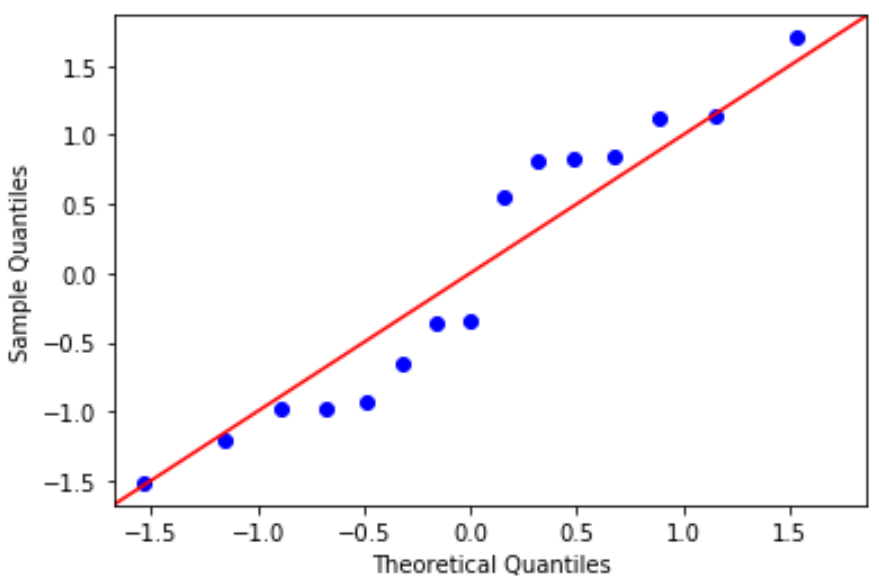
Залишки трохи відхиляються від лінії 45 градусів, але недостатньо, щоб викликати серйозне занепокоєння. Ми можемо припустити, що припущення нормальності виконується.
Оскільки залишки є нормально розподіленими та гомоскедастичними, ми перевірили, чи виконуються припущення моделі простої лінійної регресії. Таким чином, вихід нашої моделі надійний.
Повний код Python, використаний у цьому посібнику, можна знайти тут .