Як виконати просту лінійну регресію в sas

Проста лінійна регресія — це техніка, яку ми можемо використати, щоб зрозуміти взаємозв’язок між змінною предиктором і змінною відповіді .

Ця техніка знаходить рядок, який найкраще «відповідає» даним і набуває такої форми:

ŷ = b ₀ + b ₁ x

золото:

• ŷ : оцінене значення відповіді
• b ₀ : Початок лінії регресії
• b ₁ : Нахил лінії регресії

Це рівняння допомагає нам зрозуміти взаємозв’язок між змінною предиктора та змінною відповіді.

Наступний покроковий приклад показує, як виконати просту лінійну регресію в SAS.

Крок 1: Створіть дані

Для цього прикладу ми створимо набір даних, що містить загальну кількість вивчених годин і оцінку підсумкового іспиту 15 студентів.

Ми підберемо просту модель лінійної регресії, використовуючи години як змінну прогностику та оцінку як змінну відповіді.

Наступний код показує, як створити цей набір даних у SAS:

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

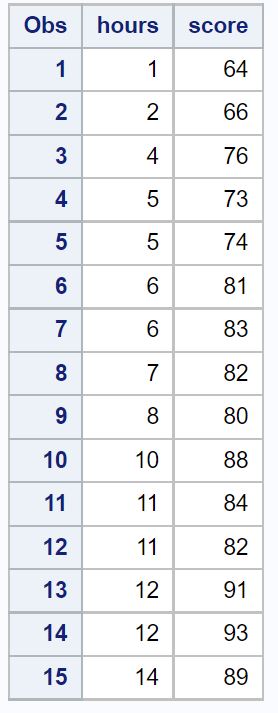
Крок 2. Підберіть просту модель лінійної регресії

Далі ми використаємо proc reg , щоб відповідати моделі простої лінійної регресії:

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

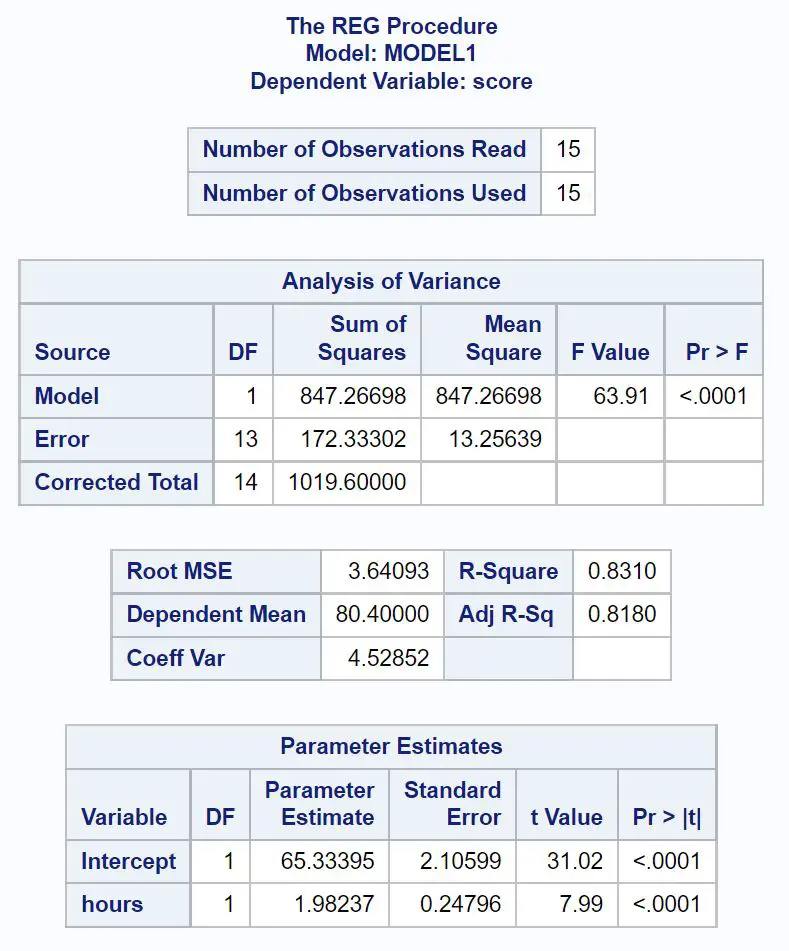
Ось як інтерпретувати найважливіші значення з кожної таблиці в результаті:

Таблиця аналізу прогалин:

Загальне F-значення регресійної моделі становить 63,91 , а відповідне значення p <0,0001 .

Оскільки це p-значення менше 0,05, ми робимо висновок, що регресійна модель в цілому є статистично значущою. Іншими словами, години є корисною змінною для прогнозування результатів іспиту.

Модельний стіл:

Значення R-квадрат говорить нам про відсоток варіації оцінок іспиту, який можна пояснити кількістю вивчених годин.

Загалом, чим більше значення R-квадрат регресійної моделі, тим краще прогностичні змінні прогнозують значення змінної відповіді.

У цьому випадку 83,1% варіації оцінок на іспитах можна пояснити кількістю вивчених годин. Це значення досить високе, вказуючи на те, що вивчені години є дуже корисною змінною для прогнозування результатів іспиту.

Таблиця оцінок параметрів:

З цієї таблиці ми можемо побачити відповідне рівняння регресії:

Оцінка = 65,33 + 1,98*(години)

Ми інтерпретуємо це так, що кожна додаткова вивчена година пов’язана із середнім збільшенням оцінки іспиту на 1,98 бала .

Початкове значення говорить нам, що середній іспитовий бал для студента, який навчається нуль годин, становить 65,33 .

Ми також можемо використати це рівняння, щоб знайти очікуваний бал за іспит на основі кількості годин, які навчається студент.

Наприклад, студент, який навчається 10 годин, повинен набрати іспитовий бал 85,13 :

Оцінка = 65,33 + 1,98*(10) = 85,13

Оскільки p-значення (<0,0001) для годин менше 0,05 у цій таблиці, ми робимо висновок, що це статистично значуща змінна предиктора.

Крок 3: Аналіз залишкових ділянок

Проста лінійна регресія робить два важливі припущення щодо залишків моделі:

• Залишки розподіляються нормально.
• Залишки мають однакову дисперсію (« гомоскедастичність ») на кожному рівні змінної предиктора.

Якщо ці припущення не виконуються, то результати нашої моделі регресії можуть бути ненадійними.

Щоб переконатися, що ці припущення виконуються, ми можемо проаналізувати залишкові графіки, які SAS автоматично відображає у вихідних даних:

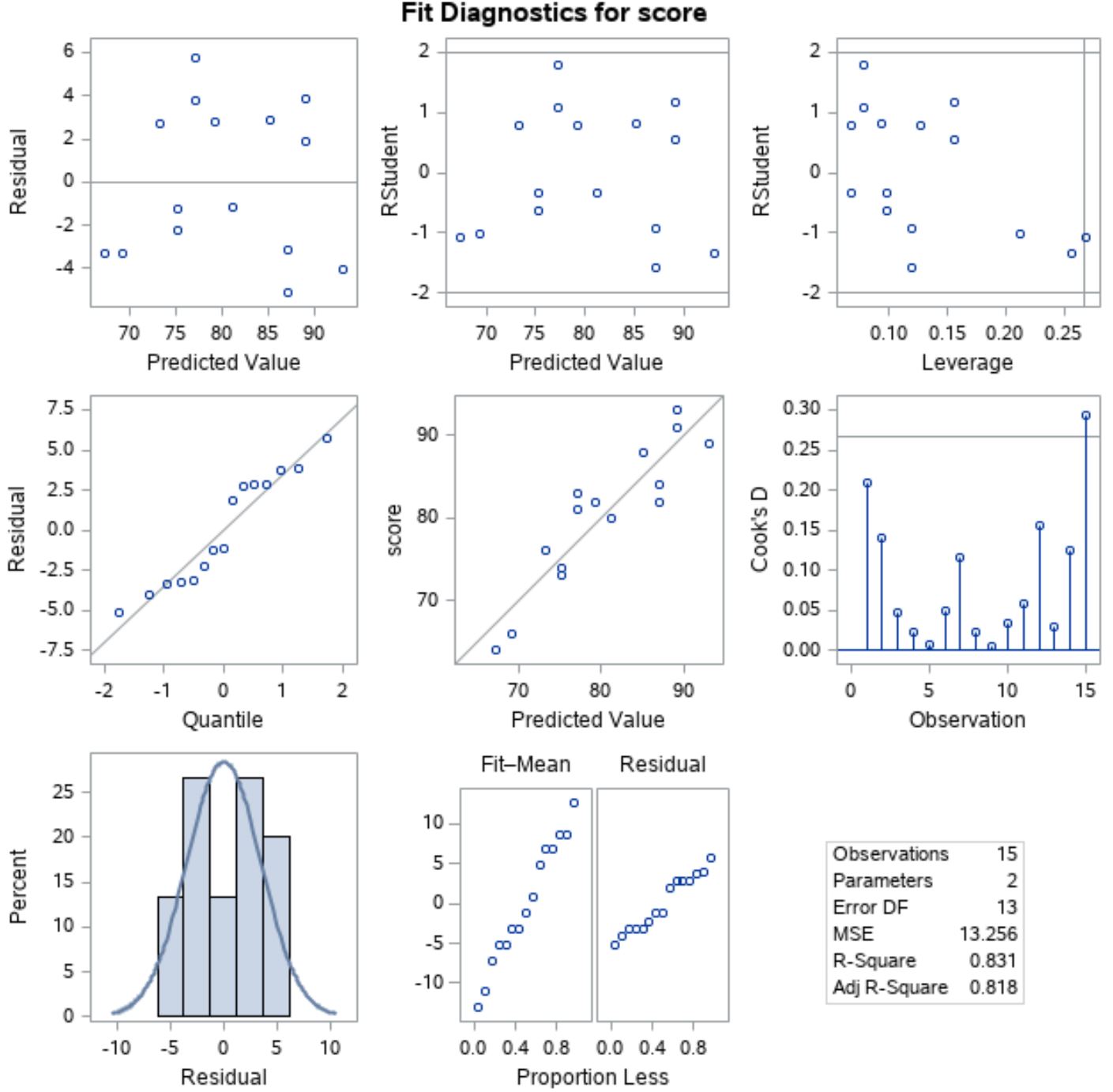
Щоб переконатися, що залишки розподілені нормально , ми можемо проаналізувати графік у лівій позиції середньої лінії з «Квантилем» уздовж осі х і «Залишком» уздовж осі у.

Цей графік називається графіком QQ , що скорочується від «квантиль-квантиль», і використовується для визначення того, чи дані розподілені нормально чи ні. Якщо дані розподілені нормально, точки на графіку QQ лежатимуть на прямій діагональній лінії.

З графіка ми бачимо, що точки лежать приблизно вздовж прямої діагональної лінії, тому можна вважати, що залишки розподілені нормально.

Далі, щоб переконатися, що залишки є гомоскедастичними , ми можемо подивитися на графік у лівій позиції першого рядка з «Передбачуваним значенням» уздовж осі x і «Залишком» уздовж осі y.

Якщо точки на графіку випадково розкидані навколо нуля без чіткого шаблону, тоді можна припустити, що залишки є гомоскедастичними.

З графіка ми бачимо, що точки розкидані навколо нуля випадковим чином з приблизно однаковою дисперсією на кожному рівні по всьому графіку, тому ми можемо припустити, що залишки гомоскедастичні.

Оскільки виконано обидва припущення, ми можемо припустити, що результати моделі простої лінійної регресії надійні.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в SAS:

Як виконати односторонній дисперсійний аналіз у SAS
Як виконати двосторонній дисперсійний аналіз у SAS
Як розрахувати кореляцію в SAS