Процентиль, квартиль і квантиль: у чому різниця?

Три терміни, які студенти часто плутають у статистиці, це процентили, квартилі та квантилі.

Ось просте визначення кожного:

Процентилі: діапазон від 0 до 100.

Квартилі: діапазон від 0 до 4.

Квантилі: перехід від будь-якого значення до будь-якого іншого значення.

Зауважте, що процентілі та квартилі — це просто типи квантилів.

Деякі типи квантилів навіть мають спеціальні назви, зокрема:

• 4 квантилі називаються квартилями .
• 5 квантилів називаються квінтилями .
• 8 квантилів називаються октилями .
• 10 квантилів називаються децилями .
• 100 квантилів називаються процентилями .

Зауважте, що процентилі та квартилі мають таке співвідношення:

• 0 процентиль = 0 квартиль (також називається мінімумом)
• 25-й процентиль = 1-й квартиль
• 50-й процентиль = 2-й квартиль (також називається медіаною)
• 75-й процентиль = 3-й квартиль
• 100-й процентиль = 4-й квартиль (також званий максимумом)

Приклад: визначення процентилів і квартилів

Припустімо, що ми маємо такий набір даних із 20 значеннями:

Використовуючи статистичне програмне забезпечення (наприклад, Excel, R, Python тощо), ми можемо знайти такі процентилі та квартилі для цього набору даних:

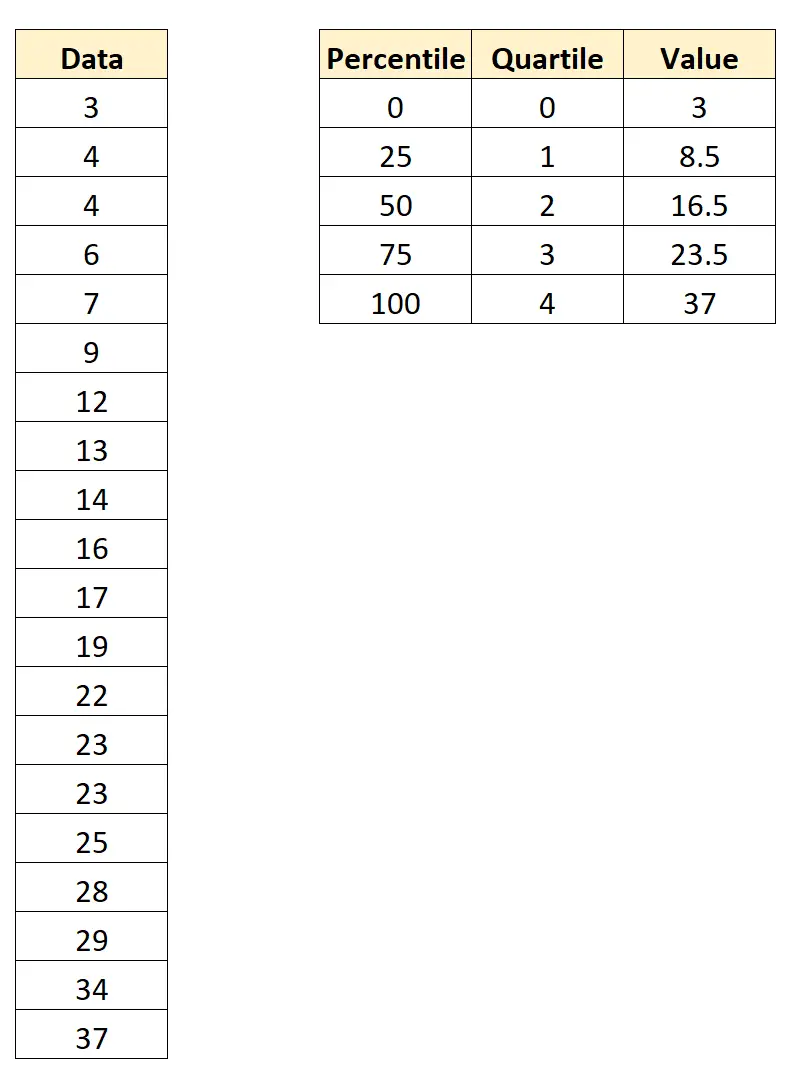
Ось як інтерпретувати ці значення:

• Процентиль 0 і квартиль 0 дорівнюють 3 .
• 25-й процентиль і 1-й квартиль дорівнюють 8,5 .
• 50-й процентиль і 2-й квартиль дорівнює 16,5 .
• 75-й процентиль і 3-й квартиль дорівнює 23,5 .
• 100-й процентиль і 4-й квартиль дорівнюють 37 .

Коли використовувати процентилі проти квартилів

Процентилі можна використовувати, щоб відповісти на такі запитання, як:

Скільки потрібно набрати студенту за певний тест, щоб увійти до 10% найкращих?

Щоб відповісти на це запитання, ми знайшли б 90-й процентиль усіх балів, тобто значення, яке відокремлює нижні 90% від 10 найвищих.

Який зріст охоплює 40% середнього зросту учнів конкретної школи?

Щоб відповісти на це запитання, ми знайшли б 70-й процентиль зросту та 30-й процентиль зросту, які є двома значеннями, які визначають верхню та нижню межі для середніх 40% зросту.

Квартилі можна використовувати для відповідей на такі запитання, як:

Скільки студент повинен набрати на тесті, щоб потрапити в першу чверть балів?

Щоб відповісти на це запитання, ми знайшли б 3-й квартиль усіх балів, який є значенням, яке відокремлює нижні 75% від 25% найвищих.

Що таке інтерквартильний діапазон даного набору даних?

Інтерквартильний діапазон (IQR) – це діапазон середніх 50% значень даних. Щоб знайти IQR для заданого набору даних, ми можемо обчислити 3-й квартиль – 1-й квартиль.

Додаткові ресурси

Як обчислити процентиль у R
Як обчислити квартилі в R
Як обчислити інтерквартильний діапазон в Excel
Як обчислити інтерквартильний діапазон на калькуляторі TI-84