Як виконати тест wilcoxon signed rank

Тест Вілкоксона зі знаком рангу є непараметричною версією парного t-критерію . Він використовується, щоб перевірити, чи існує значна різниця між двома середніми сукупностями.

Коли використовувати знаковий ранговий тест Вілкоксона

Використовуйте тест Wilcoxon Signed Rank, якщо ви бажаєте використати парний t-тест, але розподіл відмінностей між парами є дуже ненормальним .

Найпростіший спосіб визначити, чи відмінності розподілені ненормально, — це створити гістограму відмінностей і побачити, чи відповідають вони певній мірі нормальному розподілу у формі «дзвіночка».

Майте на увазі, що парний t-тест досить стійкий до відхилень від нормальності, тому відхилення від нормального розподілу має бути достатньо великим, щоб виправдати використання тесту Wilcoxon Signed Rank.

Як пройти Тест на ранг Wilcoxon Signed

У наступному прикладі показано, як виконати тест Wilcoxon Signed Rank.

Баскетбольний тренер хоче знати, чи певна тренувальна програма збільшує кількість штрафних кидків, які виконують його гравці. Щоб перевірити це, він попросив 15 гравців виконати по 20 штрафних кидків до і після програми тренувань.

Оскільки кожен гравець може бути «в парі» сам із собою, тренер планував використати парний t-тест, щоб визначити, чи є значна різниця між середньою кількістю штрафних кидків, виконаних до та після програми тренувань. навчання.

Однак розподіл відмінностей виявляється ненормальним, тому замість нього тренер використовує знаковий ранговий тест Вілкоксона.

У наступній таблиці представлено кількість штрафних кидків (з 20 спроб) кожним із 15 гравців до та після програми тренувань:

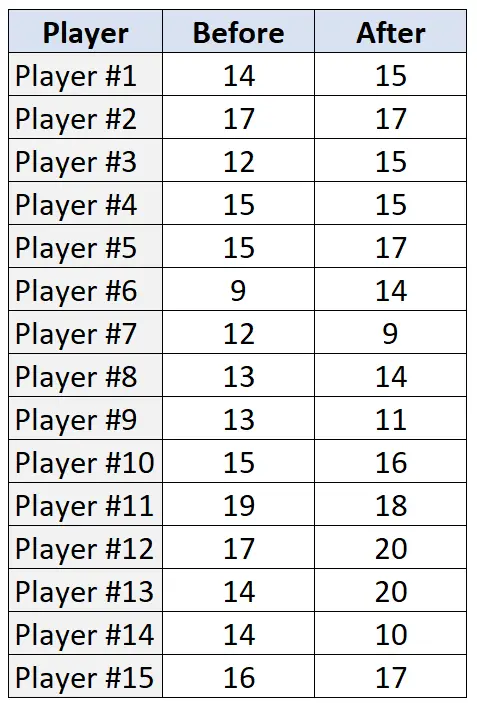
Крок 1: Сформулюйте нульову та альтернативну гіпотези.

H ₀ : Середня різниця між двома групами дорівнює нулю.

H _A : Середня різниця від’ємна. (наприклад, гравці виконують менше штрафних кидків перед тим, як взяти участь у навчальній програмі)

Крок 2: Знайдіть різницю та абсолютну різницю для кожної пари.

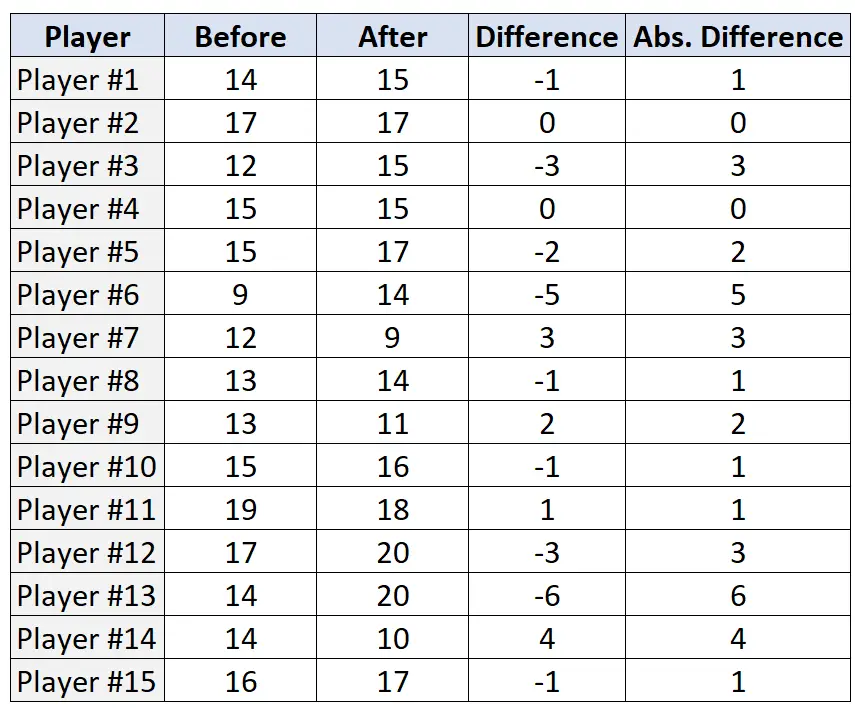
Крок 3: ранжуйте пари на основі абсолютних різниць і призначте ранг від найменшої до найбільшої абсолютної різниці. Ігноруйте пари, які мають абсолютну різницю «0», і призначайте середні ранги в разі нічиєї.

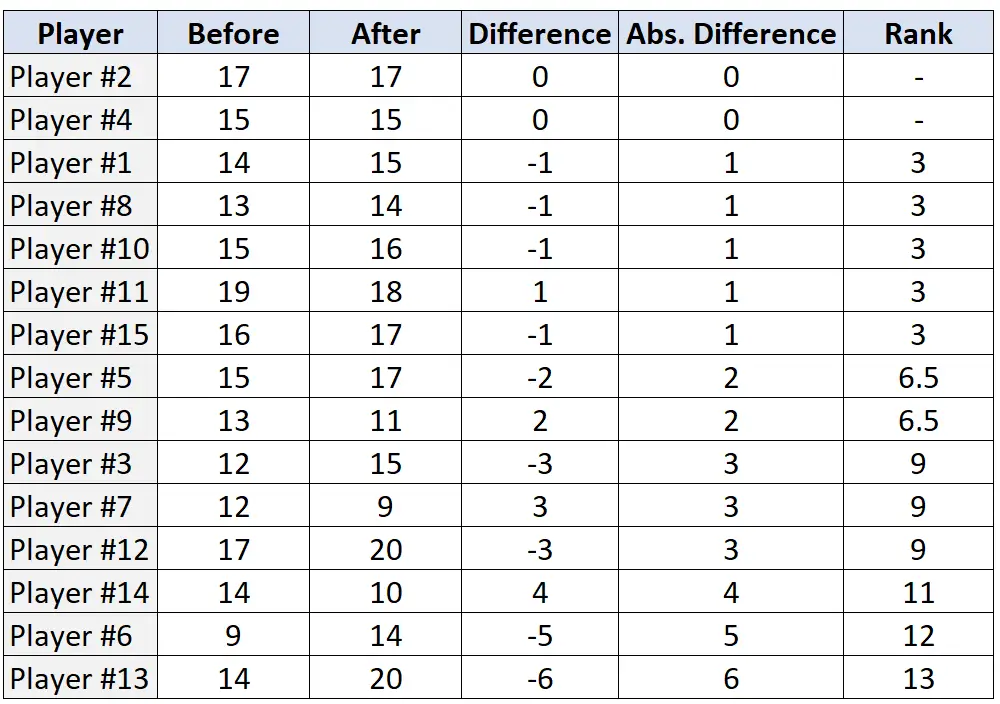
Крок 4: Знайдіть суму позитивних і негативних рангів.

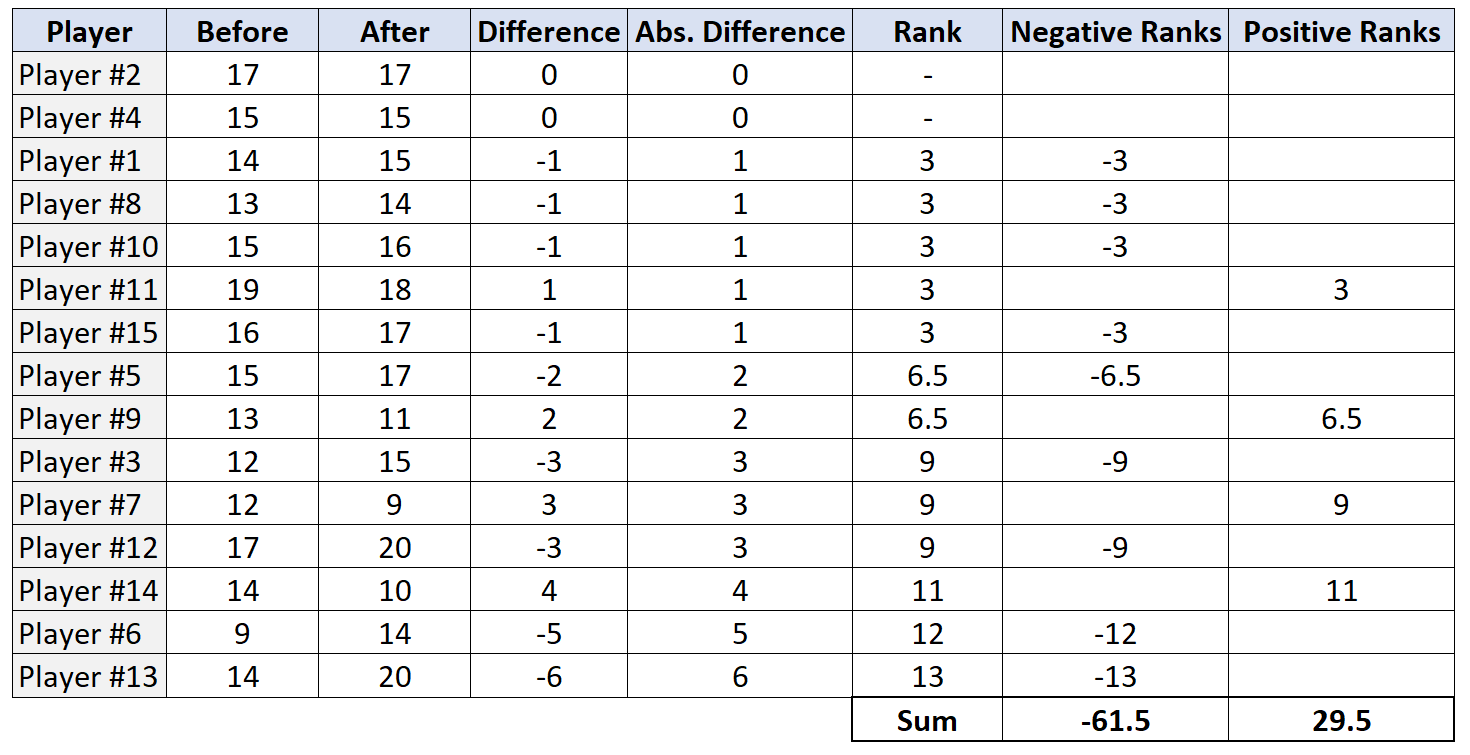
Крок 5: Відкинути або не відхилити нульову гіпотезу.

Тестова статистика, W, є найменшим з абсолютних значень позитивних рангів і негативних рангів. У цьому випадку найменше значення дорівнює 29,5. Отже, наша тестова статистика W = 29,5 .

Щоб визначити, чи слід відхиляти нульову гіпотезу, ми можемо звернутися до критичного значення, знайденого в таблиці критичних значень тесту Вілкоксона на ранговий знак, яке відповідає n і вибраному альфа-рівню.

Якщо наша тестова статистика W менша або дорівнює критичному значенню в таблиці, ми можемо відхилити нульову гіпотезу. Інакше ми не зможемо відхилити нульову гіпотезу.

Критичне значення, яке відповідає альфа-рівню 0,05 і n = 13 (загальна кількість пар мінус дві, для яких ми не розрахували ранг, оскільки вони мали спостережувану різницю 0), становить 17 .

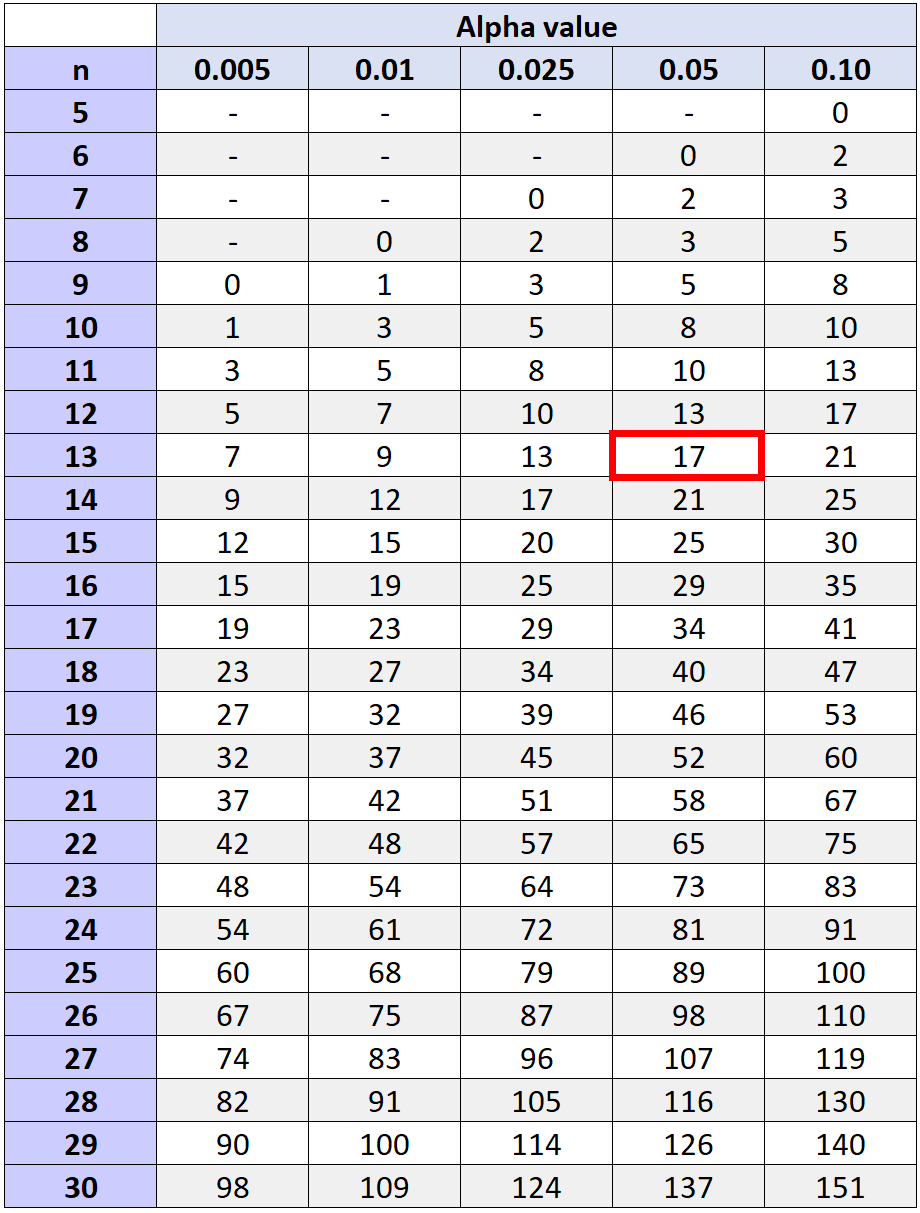
Оскільки наша тестова статистика (W = 29,5) не менше або дорівнює 17, ми не можемо відхилити нульову гіпотезу. У нас немає достатніх доказів того, що тренувальна програма призводить до значного збільшення кількості штрафних кидків гравців.

Примітка. Використовуйте Wilcoxon Signed Rank Test Calculator , якщо ви хочете виконати тест за допомогою калькулятора, а не вручну.