Регресія через початок координат: визначення та приклад
Проста лінійна регресія — це метод, який можна використовувати для кількісної оцінки зв’язку між однією або декількома змінними предиктора та змінною відповіді .
Проста модель лінійної регресії має такий вигляд:
y = β 0 + β 1 x
золото:
- y : значення змінної відповіді
- β 0 : значення змінної відповіді, коли x = 0 (називається терміном «перехоплення»)
- β 1 : середнє збільшення змінної відповіді, пов’язане зі збільшенням x на одну одиницю
- x : значення передбачуваної змінної
Модифікована версія цієї моделі відома як регресія через початок координат , яка змушує y дорівнювати 0, коли x дорівнює 0.
Цей тип моделі має наступний вигляд:
y = β1x
Зверніть увагу, що термін перехоплення було повністю видалено з моделі.
Ця модель іноді використовується, коли дослідники знають, що змінна відповіді має дорівнювати нулю, коли змінна предиктора дорівнює нулю.
У реальному світі цей тип моделі найчастіше використовується в лісівництві або екологічних дослідженнях .
Наприклад, дослідники можуть використовувати окружність дерева, щоб передбачити висоту дерева. Якщо дане дерево має нульову окружність, воно повинно мати нульову висоту.
Таким чином, при підгонці регресійної моделі до цих даних не буде сенсу, щоб вихідний член був ненульовим.
У наступному прикладі показано різницю між підгонкою звичайної простої моделі лінійної регресії та моделлю, яка реалізує регресію через початок координат.
Приклад: регресія через початок координат
Припустімо, що біолог хоче підібрати регресійну модель, використовуючи окружність дерева для прогнозування висоти дерева. Вона виходить і збирає такі вимірювання для зразка з 15 дерев:
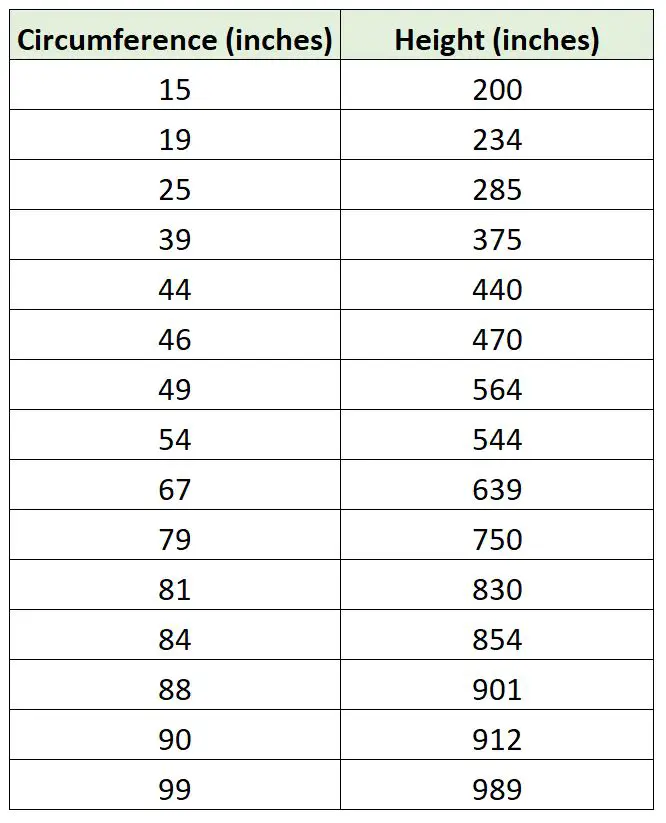
Ми можемо використати наступний код у R, щоб узгодити просту модель лінійної регресії з моделлю регресії, яка не використовує перехоплення, і побудувати дві лінії регресії:
#create data frame df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99), height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854, 901, 912, 989)) #fit a simple linear regression model model <- lm(height ~ circ, data = df) #fit regression through the origin model_origin <- lm(height ~ 0 + ., data = df) #create scatterplot plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ', cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100)) #add the fitted regression lines to the scatterplot abline(model, col=' blue ', lwd= 2 ) abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )
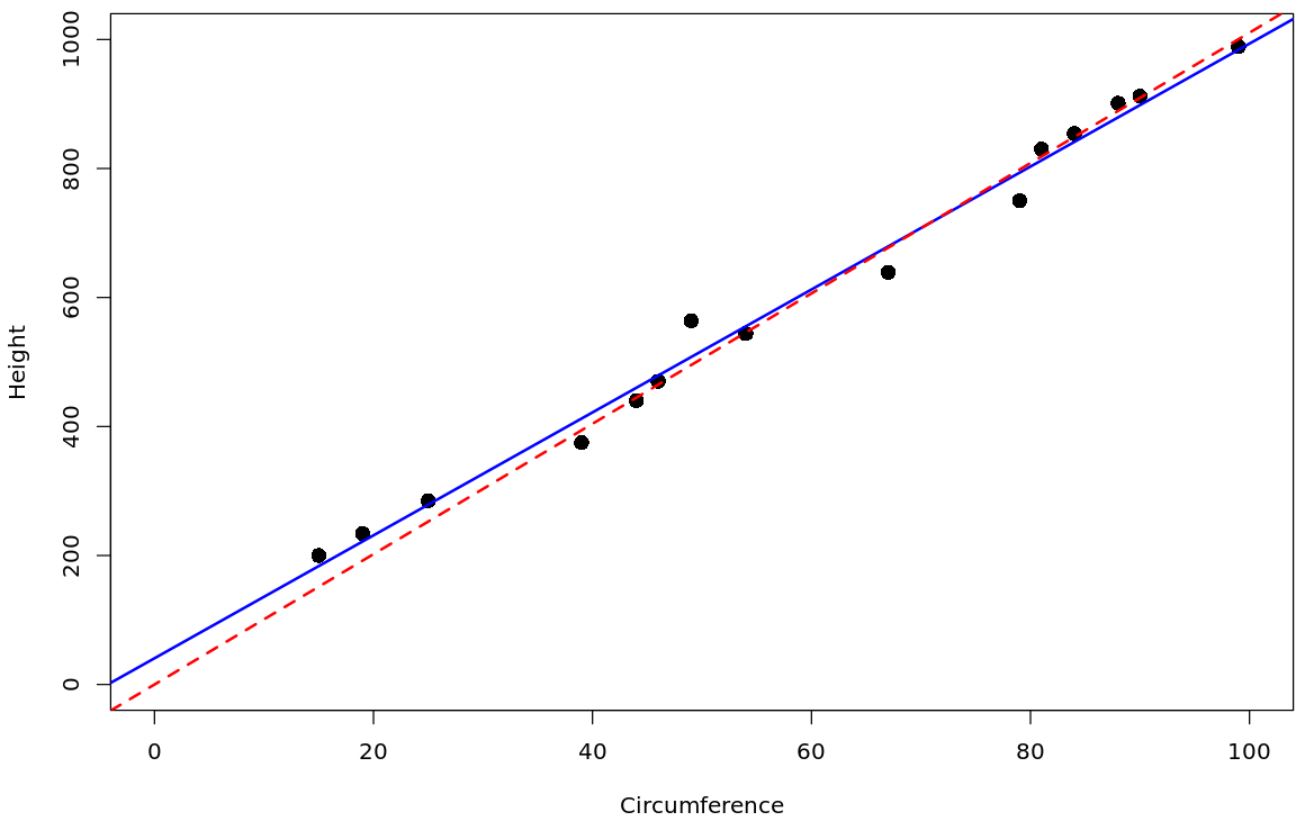
Червона пунктирна лінія представляє регресійну модель, яка проходить через початок координат, а синя суцільна лінія представляє звичайну просту модель лінійної регресії.
Ми можемо використовувати такий код у R, щоб отримати оцінки коефіцієнтів для кожної моделі:
#display coefficients for simple linear regression model coef(model) (Intercept) circ 40.696971 9.529631 #display coefficients for regression model through the origin coef(model_origin) circ 10.10574
Підігнане рівняння для моделі простої лінійної регресії виглядає так:
Висота = 40,6969 + 9,5296 (обхват)
А підігнане рівняння для моделі регресії через початок координат:
Висота = 10,1057 (обхват)
Зверніть увагу, що оцінки коефіцієнтів для змінної окружності дещо відрізняються.
Застереження щодо використання регресії через джерело
Перш ніж використовувати регресію перехоплення, ви повинні бути абсолютно впевнені, що значення 0 для змінної предиктора передбачає значення 0 для змінної відповіді. У багатьох ситуаціях це майже неможливо знати напевно.
І якщо ви використовуєте регресію через джерело, щоб зберегти ступінь свободи в оцінці джерела, це рідко має суттєве значення, якщо розмір вашої вибірки достатньо великий.
Якщо ви вирішите використовувати регресію через джерело, обов’язково викладіть свої міркування в остаточному аналізі або звіті.
Додаткові ресурси
У наступних посібниках надається додаткова інформація про лінійну регресію.
Вступ до простої лінійної регресії
Вступ до множинної лінійної регресії
Як читати та інтерпретувати таблицю регресії