Введення в регресію ріджа

У звичайній множинній лінійній регресії ми використовуємо набір із p предикторних змінних і змінну відповіді , щоб відповідати моделі такого вигляду:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

золото:

• Y : змінна відповіді
• X _j : j- ^та прогнозна змінна
• β _j : середній вплив на Y від збільшення X _j на одну одиницю, утримуючи всі інші предиктори фіксованими
• ε : термін помилки

Значення β ₀ , β ₁ , B ₂ , …, β _p вибираються методом найменших квадратів , який мінімізує суму квадратів нев’язок (RSS):

RSS = Σ(y _i – ŷ _i ) ²

золото:

• Σ : грецький символ, що означає суму
• y _i : фактичне значення відповіді для ^i-го спостереження
• ŷ _i : прогнозоване значення відповіді на основі моделі множинної лінійної регресії

Однак, коли прогностичні змінні сильно корельовані, мультиколінеарність може стати проблемою. Це може зробити оцінки коефіцієнтів моделі ненадійними та мати високу дисперсію.

Один із способів обійти цю проблему без повного видалення певних змінних прогнозу з моделі полягає в застосуванні методу, відомого як гребенева регресія , який натомість прагне мінімізувати наступне:

RSS + λΣβ _j ²

де j змінюється від 1 до p і λ ≥ 0.

Цей другий член у рівнянні відомий як штраф за вилучення .

Коли λ = 0, цей штрафний термін не має ефекту, і гребенева регресія дає ті самі оцінки коефіцієнта, що й метод найменших квадратів. Однак, коли λ наближається до нескінченності, штраф за скорочення стає більш впливовим і оцінки пікового коефіцієнта регресії наближаються до нуля.

Загалом найменш впливові прогностичні змінні в моделі будуть знижуватися до нуля найшвидше.

Навіщо використовувати регресію Ріджа?

Перевага регресії Ріджа над регресією найменших квадратів полягає в компромісі зміщення-дисперсії .

Пам’ятайте, що середня квадратична помилка (MSE) – це показник, який ми можемо використовувати для вимірювання точності даної моделі, і він обчислюється таким чином:

MSE = Var( f̂( x ₀ )) + [Зміщення( f̂( x ₀ ))] ² + Var(ε)

MSE = дисперсія + зсув ² + незнижувана помилка

Основна ідея регресії Ріджа полягає в тому, щоб ввести невелике зміщення, щоб дисперсію можна було значно зменшити, що призвело б до нижчого загального MSE.

Щоб проілюструвати це, розглянемо наступний графік:

Зверніть увагу, що зі збільшенням λ дисперсія значно зменшується з дуже невеликим збільшенням зміщення. Однак після певної точки дисперсія зменшується менш швидко і зменшення коефіцієнтів призводить до їх значного недооцінювання, що призводить до різкого збільшення зміщення.

З графіка ми бачимо, що MSE тесту є найнижчим, коли ми вибираємо значення для λ, яке забезпечує оптимальний компроміс між упередженням і дисперсією.

Коли λ = 0, штрафний термін у хребтовій регресії не має ефекту, тому дає ті самі оцінки коефіцієнта, що й найменші квадрати. Однак, збільшивши λ до певної точки, ми можемо зменшити загальну MSE тесту.

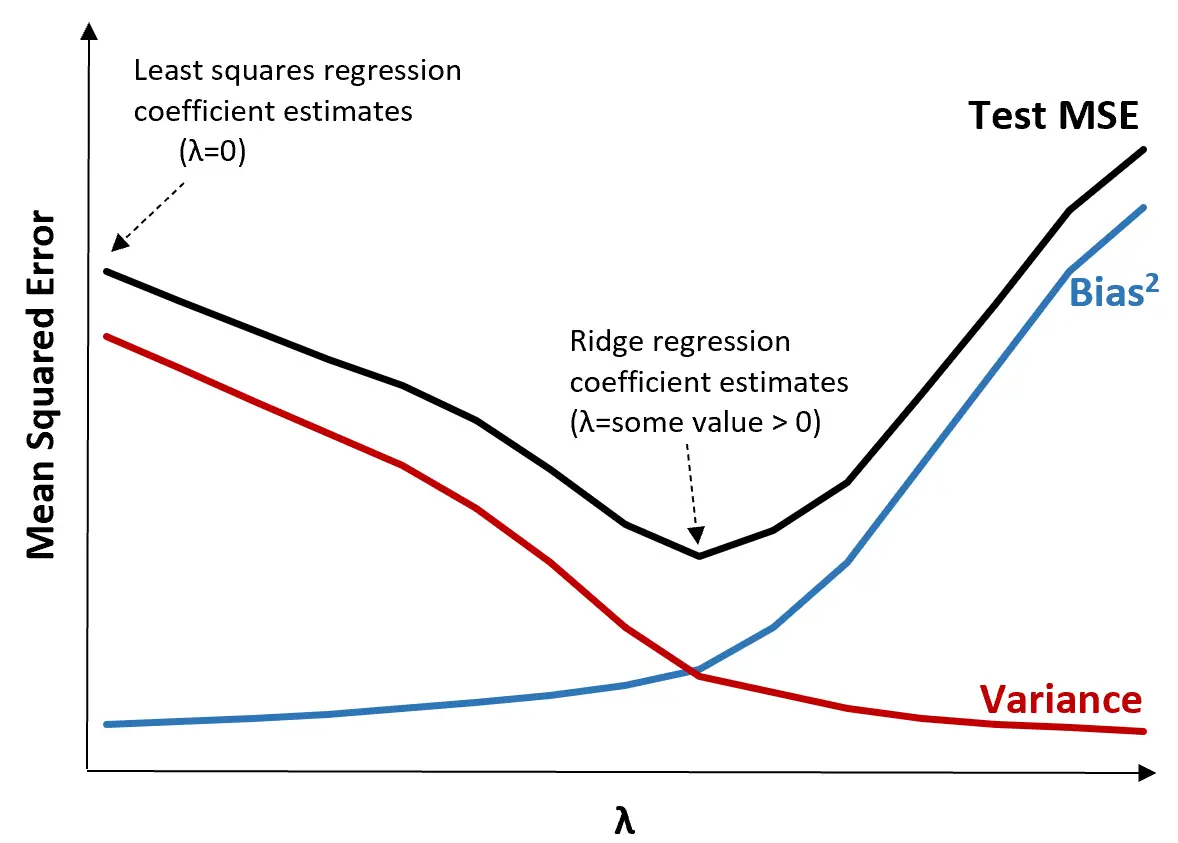
Це означає, що підгонка моделі за допомогою хребтової регресії призведе до менших помилок тестування, ніж підгонка моделі за допомогою регресії найменших квадратів.

Етапи виконання хребтової регресії на практиці

Для виконання регресії хребта можна використовувати такі кроки:

Крок 1: обчисліть кореляційну матрицю та значення VIF для змінних предиктора.

По-перше, нам потрібно створити кореляційну матрицю та обчислити значення VIF (коефіцієнт інфляції дисперсії) для кожної змінної предиктора.

Якщо ми виявимо сильну кореляцію між змінними предикторів і високими значеннями VIF (деякі тексти визначають «високе» значення VIF як 5, тоді як інші використовують 10), тоді гребенева регресія, ймовірно, підходить.

Однак, якщо в даних немає мультиколінеарності, може не знадобитися спочатку виконувати гребневу регресію. Замість цього ми можемо виконати звичайну регресію методом найменших квадратів.

Крок 2: Стандартизуйте кожну змінну предиктора.

Перед виконанням хребтової регресії нам потрібно масштабувати дані таким чином, щоб кожна змінна предиктора мала середнє значення 0 і стандартне відхилення 1. Це гарантує, що жодна змінна предиктора не матиме надмірного впливу під час виконання хребтової регресії.

Крок 3: Підберіть модель хребтової регресії та виберіть значення для λ.

Немає точної формули, яку ми можемо використати, щоб визначити, яке значення використовувати для λ. На практиці існує два поширених способи вибору λ:

(1) Створіть графік хребта. Це графік, який візуалізує значення оцінок коефіцієнта при зростанні λ до нескінченності. Як правило, ми вибираємо λ як значення, при якому більшість оцінок коефіцієнтів починають стабілізуватися.

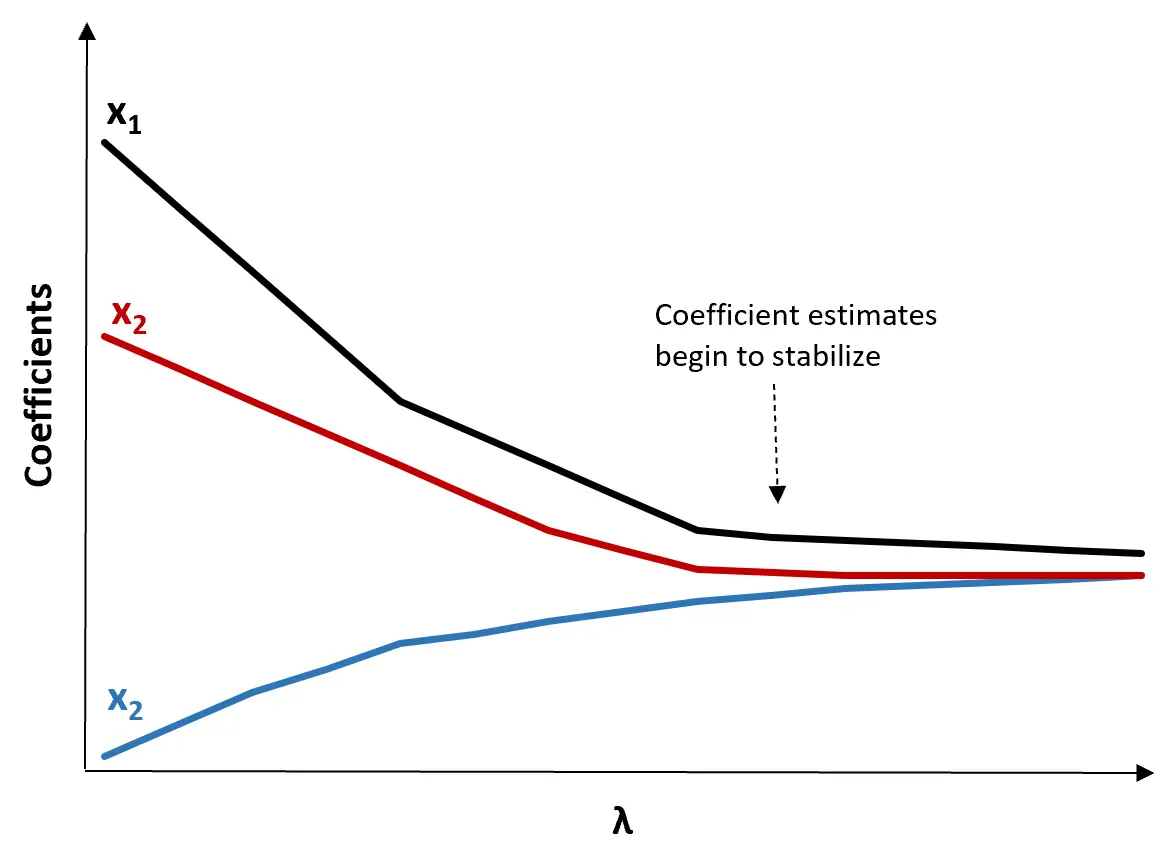
(2) Обчисліть тест MSE для кожного значення λ.

Інший спосіб вибрати λ – це просто обчислити тестову MSE кожної моделі з різними значеннями λ і вибрати λ як значення, яке дає найнижчу тестову MSE.

Переваги та недоліки хребтової регресії

Найбільшою перевагою регресії Ріджа є її здатність давати нижчу середню квадратичну помилку (MSE), ніж метод найменших квадратів, коли присутня мультиколінеарність.

Однак найбільшим недоліком регресії Ріджа є її нездатність виконувати вибір змінних, оскільки вона включає всі змінні предикторів у кінцевій моделі. Оскільки деякі предиктори будуть зменшені дуже близько до нуля, це може ускладнити інтерпретацію результатів моделі.

На практиці регресія Ріджа має потенціал створити модель, здатну робити кращі прогнози порівняно з моделлю найменших квадратів, але часто важче інтерпретувати результати моделі.

Залежно від того, чи важливіша для вас інтерпретація моделі чи точність прогнозу, ви можете використовувати звичайний метод найменших квадратів або хребетну регресію в різних сценаріях.

Регресія Ridge в R & Python

У наведених нижче посібниках пояснюється, як виконати гребневу регресію в R і Python, двох мовах, які найчастіше використовуються для підгонки моделей гребневої регресії:

Регресія хребта в R (покроково)
Регресія Ridge в Python (крок за кроком)