Регресія хребта в r (крок за кроком)

Ридж-регресія — це метод, який ми можемо використовувати для підгонки регресійної моделі, коли в даних присутня мультиколінеарність .

У двох словах, регресія методом найменших квадратів намагається знайти оцінки коефіцієнтів, які мінімізують залишкову суму квадратів (RSS):

RSS = Σ(y _i – ŷ _i )2

золото:

• Σ : грецький символ, що означає суму
• y _i : фактичне значення відповіді для ^i-го спостереження
• ŷ _i : прогнозоване значення відповіді на основі моделі множинної лінійної регресії

І навпаки, гребенева регресія прагне мінімізувати наступне:

RSS + λΣβ _j ²

де j переходить від 1 до p предикторних змінних і λ ≥ 0.

Цей другий член у рівнянні відомий як штраф за вилучення . У гребеневій регресії ми вибираємо значення для λ, яке дає найменший можливий тест MSE (середня квадратична помилка).

У цьому підручнику наведено покроковий приклад того, як виконати гребеневу регресію в R.

Крок 1. Завантажте дані

Для цього прикладу ми використаємо вбудований набір даних R під назвою mtcars . Ми будемо використовувати hp як змінну відповіді та наступні змінні як предиктори:

• миль на галлон
• вага
• лайно
• qsec

Для виконання гребневої регресії ми будемо використовувати функції з пакету glmnet . Цей пакет вимагає, щоб змінна відповіді була вектором, а набір змінних предикторів належав до класу data.matrix .

Наступний код показує, як визначити наші дані:

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

Крок 2: Підберіть регресійну модель Ріджа

Далі ми використаємо функцію glmnet() , щоб відповідати регресійній моделі Ridge і вкажемо alpha=0 .

Зауважте, що встановлення значення альфа, що дорівнює 1, еквівалентно використанню регресії Ласо, а встановлення значення альфа між 0 і 1 еквівалентно використанню еластичної мережі.

Також зауважте, що гребенева регресія вимагає стандартизації даних таким чином, щоб кожна змінна предиктора мала середнє значення 0 і стандартне відхилення 1.

На щастя, glmnet() автоматично виконує цю стандартизацію за вас. Якщо ви вже стандартизували змінні, ви можете вказати standardize=False .

 library (glmnet)

#fit ridge regression model
model <- glmnet(x, y, alpha = 0 )

#view summary of model
summary(model)

          Length Class Mode   
a0 100 -none- numeric
beta 400 dgCMatrix S4     
df 100 -none- numeric
dim 2 -none- numeric
lambda 100 -none- numeric
dev.ratio 100 -none- numeric
nulldev 1 -none- numeric
npasses 1 -none- numeric
jerr 1 -none- numeric
offset 1 -none- logical
call 4 -none- call   
nobs 1 -none- numeric

Крок 3: Виберіть оптимальне значення лямбда

Далі ми визначимо значення лямбда, яке дає найменшу тестову середню квадратичну помилку (MSE), використовуючи k-кратну перехресну перевірку .

На щастя, glmnet має функцію cv.glmnet() , яка автоматично виконує k-кратну перехресну перевірку, використовуючи k = 10 разів.

 #perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 0 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 10.04567

#produce plot of test MSE by lambda value
plot(cv_model) 

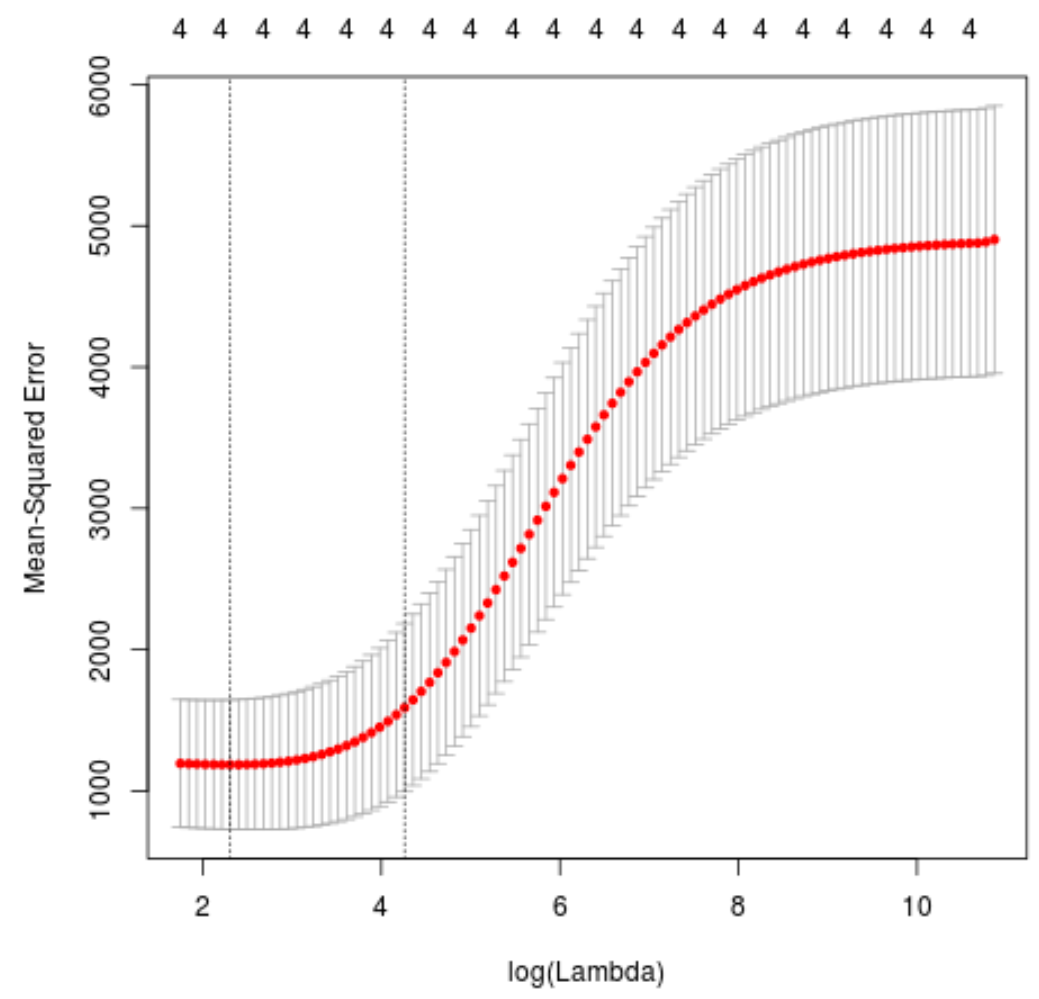
Значення лямбда, яке мінімізує тест MSE, виявляється 10,04567 .

Крок 4: Проаналізуйте остаточну модель

Нарешті, ми можемо проаналізувати кінцеву модель, створену за оптимальним значенням лямбда.

Ми можемо використати такий код, щоб отримати оцінки коефіцієнтів для цієї моделі:

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 0 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                    s0
(Intercept) 475.242646
mpg -3.299732
wt 19.431238
drat -1.222429
qsec -17.949721

Ми також можемо побудувати графік трасування, щоб візуалізувати, як змінилися оцінки коефіцієнтів через збільшення лямбда:

 #produce Ridge trace plot
plot(model, xvar = " lambda ") 

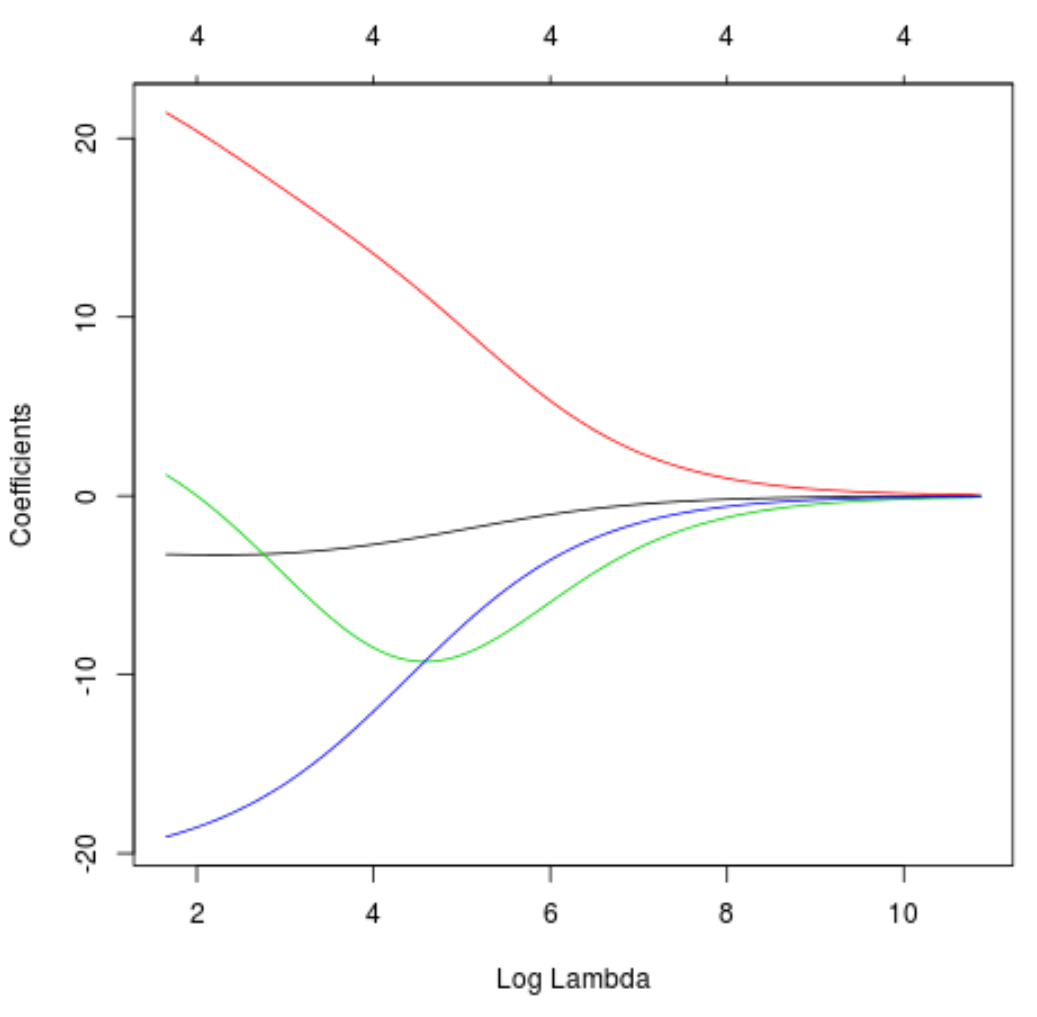
Нарешті, ми можемо розрахувати R-квадрат моделі на основі навчальних даних:

 #use fitted best model to make predictions
y_predicted <- predict (model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.7999513

R у квадраті виявляється 0,7999513 . Тобто найкраща модель змогла пояснити 79,99% варіації значень відповіді даних навчання.

Ви можете знайти повний код R, використаний у цьому прикладі , тут .