Регресія ласо в r (покроково)

Регресія ласо — це метод, який ми можемо використовувати для підгонки регресійної моделі, коли в даних присутня мультиколінеарність .

У двох словах, регресія методом найменших квадратів намагається знайти оцінки коефіцієнтів, які мінімізують залишкову суму квадратів (RSS):

RSS = Σ(y _i – ŷ _i )2

золото:

• Σ : грецький символ, що означає суму
• y _i : фактичне значення відповіді для ^i-го спостереження
• ŷ _i : прогнозоване значення відповіді на основі моделі множинної лінійної регресії

І навпаки, регресія ласо прагне мінімізувати наступне:

RSS + λΣ|β _j |

де j переходить від 1 до p предикторних змінних і λ ≥ 0.

Цей другий член у рівнянні відомий як штраф за вилучення . У ласо-регресії ми вибираємо значення для λ, яке дає найменший можливий тест MSE (середня квадратична помилка).

Цей підручник надає покроковий приклад того, як виконати регресію ласо в R.

Крок 1. Завантажте дані

Для цього прикладу ми використаємо вбудований набір даних R під назвою mtcars . Ми будемо використовувати hp як змінну відповіді та наступні змінні як предиктори:

• миль на галлон
• вага
• лайно
• qsec

Для виконання ласо-регресії ми будемо використовувати функції з пакету glmnet . Цей пакет вимагає, щоб змінна відповіді була вектором, а набір змінних предикторів належав до класу data.matrix .

Наступний код показує, як визначити наші дані:

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

Крок 2: Підберіть регресійну модель ласо

Далі ми використаємо функцію glmnet() , щоб відповідати регресійній моделі ласо та вкажемо alpha=1 .

Зауважте, що встановлення значення альфа, що дорівнює 0, еквівалентно використанню гребневої регресії , а встановлення значення альфа між 0 і 1 еквівалентно використанню еластичної сітки.  

Щоб визначити, яке значення використовувати для лямбда, ми виконаємо k-кратну перехресну перевірку та визначимо значення лямбда, яке дає найменшу тестову середньоквадратичну помилку (MSE).

Зауважте, що функція cv.glmnet() автоматично виконує k-кратну перехресну перевірку, використовуючи k = 10 разів.

 library (glmnet)

#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 5.616345

#produce plot of test MSE by lambda value
plot(cv_model) 

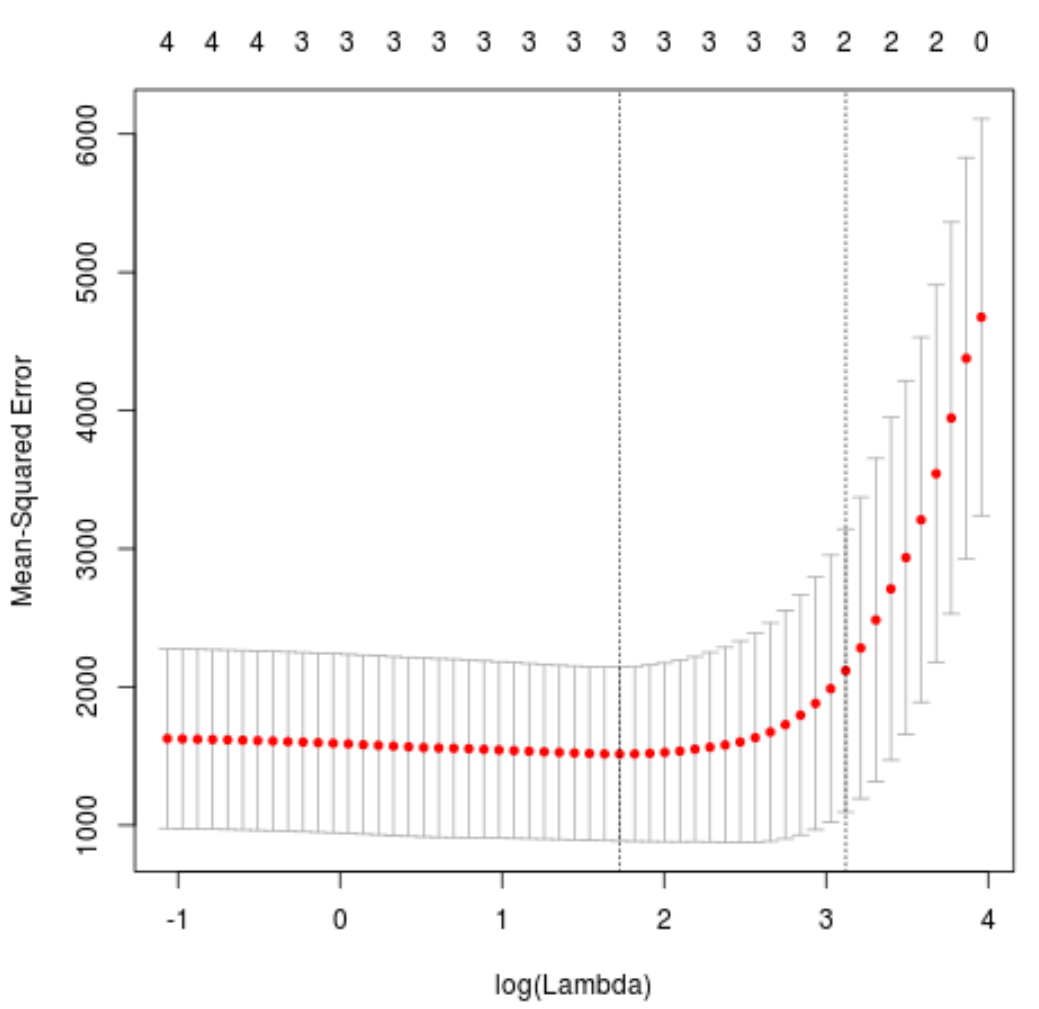
Значення лямбда, яке мінімізує тест MSE, виявляється рівним 5,616345 .

Крок 3: Проаналізуйте остаточну модель

Нарешті, ми можемо проаналізувати кінцеву модель, створену за оптимальним значенням лямбда.

Ми можемо використати такий код, щоб отримати оцінки коефіцієнтів для цієї моделі:

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                   s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.      
qsec -19.43425

Коефіцієнт для предиктора драта не показано, оскільки регресія ласо зменшила коефіцієнт до нуля. Це означає, що його повністю усунули від моделі, оскільки він не мав достатнього впливу.

Зверніть увагу, що це ключова відмінність між регресією хребта та регресією ласо . Ридж-регресія зменшує всі коефіцієнти до нуля, але ласо-регресія має потенціал для видалення предикторів із моделі, повністю зменшуючи коефіцієнти до нуля.

Ми також можемо використовувати остаточну регресійну модель ласо, щоб робити прогнози щодо нових спостережень. Наприклад, припустімо, що у нас є новий автомобіль із такими атрибутами:

• mpg: 24
• вага: 2,5
• ціна: 3,5 грн
• qsec: 18,5

У наведеному нижче коді показано, як використовувати підігнану регресійну модель ласо для прогнозування значення hp цього нового спостереження:

 #define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 ) 

#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)

[1,] 109.0842

На основі введених значень модель передбачає, що цей автомобіль матиме значення hp 109,0842 .

Нарешті, ми можемо розрахувати R-квадрат моделі на основі навчальних даних:

 #use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.8047064

R у квадраті виявляється рівним 0,8047064 . Тобто найкраща модель змогла пояснити 80,47% варіації значень відповіді тренувальних даних.

Ви можете знайти повний код R, використаний у цьому прикладі , тут .