Як виконати регресію ступеня в r (покроково)

Степенева регресія – це тип нелінійної регресії, який має таку форму:

y = ax ^b

золото:

• y: змінна відповіді
• x: передбачувана змінна
• a, b: коефіцієнти регресії, які описують зв’язок між x і y

Цей тип регресії використовується для моделювання ситуацій, коли змінна відповіді дорівнює змінній предиктора, зведеній до степеня.

Наступний покроковий приклад показує, як виконати степеневу регресію для даного набору даних у R.

Крок 1: Створіть дані

Спочатку давайте створимо фальшиві дані для двох змінних: x і y.

 #create data
x=1:20
y=c(1, 8, 5, 7, 6, 20, 15, 19, 23, 37, 33, 38, 49, 50, 56, 52, 70, 89, 97, 115)

Крок 2: Візуалізуйте дані

Далі створимо діаграму розсіювання, щоб візуалізувати зв’язок між x і y:

 #create scatterplot
plot(x, y) 

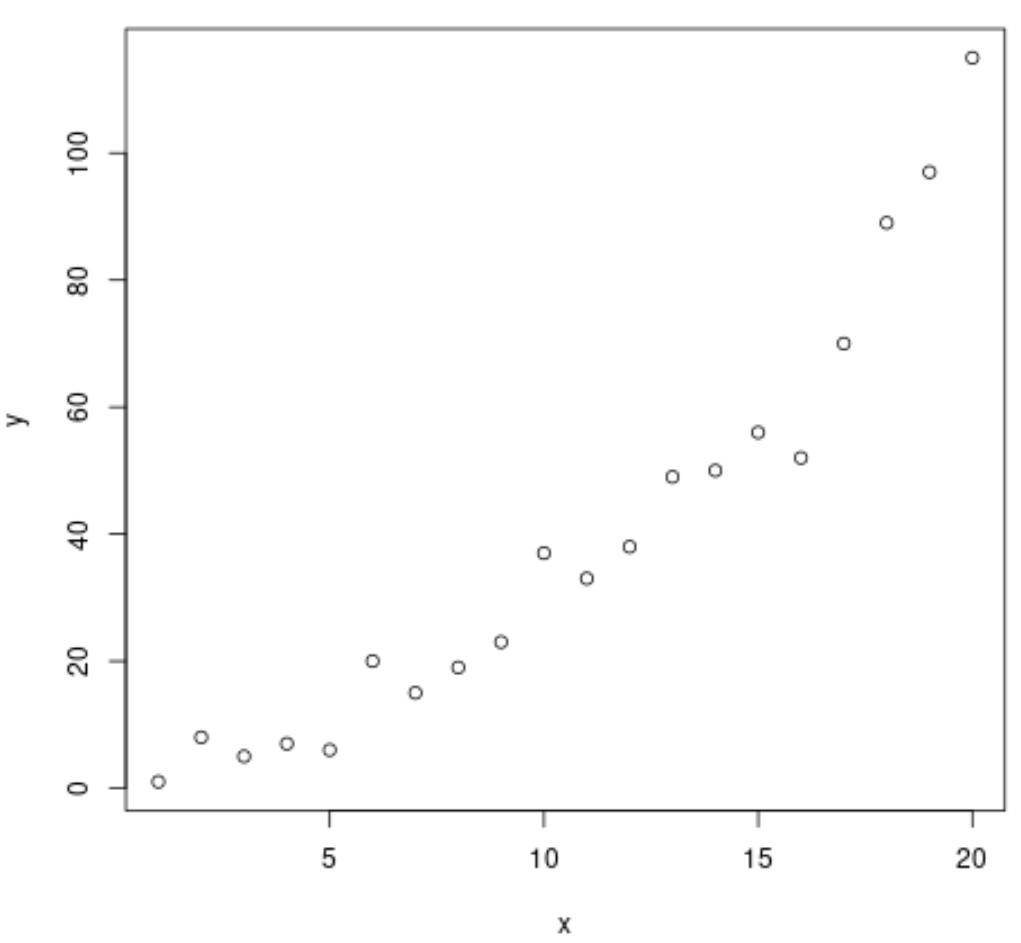
На графіку видно, що між двома змінними існує чітка залежність ступеня. Таким чином, здається розумним підібрати рівняння степеневої регресії до даних, а не модель лінійної регресії.

Крок 3: Підберіть модель регресії потужності

Далі ми використаємо функцію lm() , щоб підібрати регресійну модель до даних, вказавши, що R має використовувати журнал змінної відповіді та журнал змінної предиктора під час підгонки моделі:

 #fit the model
model <- lm(log(y)~ log(x))

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ log(x))

Residuals:
     Min 1Q Median 3Q Max 
-0.67014 -0.17190 -0.05341 0.16343 0.93186 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.15333 0.20332 0.754 0.461    
log(x) 1.43439 0.08996 15.945 4.62e-12 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3187 on 18 degrees of freedom
Multiple R-squared: 0.9339, Adjusted R-squared: 0.9302 
F-statistic: 254.2 on 1 and 18 DF, p-value: 4.619e-12

Загальне F-значення моделі становить 252,1, а відповідне значення p надзвичайно низьке (4,619e-12), що вказує на те, що модель в цілому корисна.

Використовуючи коефіцієнти з вихідної таблиці, ми можемо побачити, що підігнане рівняння степеневої регресії таке:

ln(y) = 0,15333 + 1,43439ln(x)

Застосовуючи e до обох сторін, ми можемо переписати рівняння так:

• y = e ^{0,15333 + 1,43439ln(x)}
• y = 1,1657x ^1,43439

Ми можемо використати це рівняння для прогнозування змінної відповіді y на основі значення змінної предиктора x .

Наприклад, якщо x = 12, ми передбачимо, що y дорівнюватиме 41,167 :

y = 1,1657(12) ^1,43439 = 41,167

Бонус: не соромтеся використовувати цей онлайн-калькулятор регресії потужності, щоб автоматично обчислити рівняння регресії потужності для заданого предиктора та змінної відповіді.

Додаткові ресурси

Як виконати множинну лінійну регресію в R
Як виконати експоненціальну регресію в R
Як виконати логарифмічну регресію в R