Розподіл пуассона або нормальний розподіл: у чому різниця?
Розподіл Пуассона та нормальний розподіл є двома найбільш часто використовуваними розподілами ймовірностей у статистиці.
Цей підручник містить швидке пояснення кожного дистрибутива, а також дві ключові відмінності між дистрибутивами.
Огляд: розподіл Пуассона
Розподіл Пуассона описує ймовірність отримання k успіхів протягом заданого інтервалу часу.
Якщо випадкова величина X відповідає розподілу Пуассона, то ймовірність успіху X = k можна знайти за такою формулою:
P(X=k) = λ k * e – λ / k!
золото:
- λ: середня кількість успіхів протягом певного інтервалу
- k: кількість успіхів
- e: константа, що дорівнює приблизно 2,71828
Наприклад, припустимо, що в одній лікарні в середньому відбувається 2 пологи на годину. Ми можемо використати наведену вище формулу, щоб визначити ймовірність 3 пологів за певну годину:
P(X=3) = 2 3 * e – 2/3 ! = 0,1805
Ймовірність 3 пологів за годину становить 0,1805 .
Огляд: нормальний розподіл
Нормальний розподіл описує ймовірність того, що випадкова величина приймає значення в заданому інтервалі.
Функцію щільності ймовірності нормального розподілу можна записати так:
P(X=x) = (1/σ√ 2π )e -1/2((x-μ)/σ) 2
золото:
- σ: стандартне відхилення розподілу
- μ: середнє значення розподілу
- x: значення випадкової величини
Наприклад, припустимо, що вага певного виду видр нормально розподіляється з μ = 40 фунтів і σ = 5 фунтів.
Якщо ми випадково виберемо видру з цієї популяції, ми зможемо використати таку формулу, щоб знайти ймовірність того, що вона важить від 38 до 42 фунтів:
P ( 38 < /5) 2 = 0,3108
Імовірність того, що навмання вибрана видра важить від 38 до 42 фунтів, становить 0,3108 .
Відмінність №1: стриманість проти Безперервні дані
Перша відмінність між розподілом Пуассона та нормальним розподілом полягає в типі даних, змодельованих кожним розподілом ймовірностей.
Розподіл Пуассона використовується при роботі з дискретними даними , які можуть приймати тільки цілі значення, що дорівнюють або перевищують нуль. Ось кілька прикладів:
- Кількість дзвінків, отриманих в кол-центрі за годину
- Кількість відвідувачів ресторану за день
- Кількість ДТП за місяць
У кожному сценарії випадкова змінна може приймати значення лише 0, 1, 2, 3 тощо.
Нормальний розподіл використовується під час роботи з безперервними даними , які можуть приймати будь-яке значення від негативної до позитивної нескінченності. Ось кілька прикладів:
- Вага певної тварини
- Висота певної рослини
- Час жіночого марафону
- Температура в градусах Цельсія
У цих сценаріях випадкові змінні можуть приймати будь-які значення, наприклад -11,3, 21,343435, 85 тощо.
Відмінність №2: форма розподілів
Друга відмінність розподілу Пуассона від нормального розподілу полягає у формі розподілів.
Нормальний розподіл завжди матиме форму дзвона:
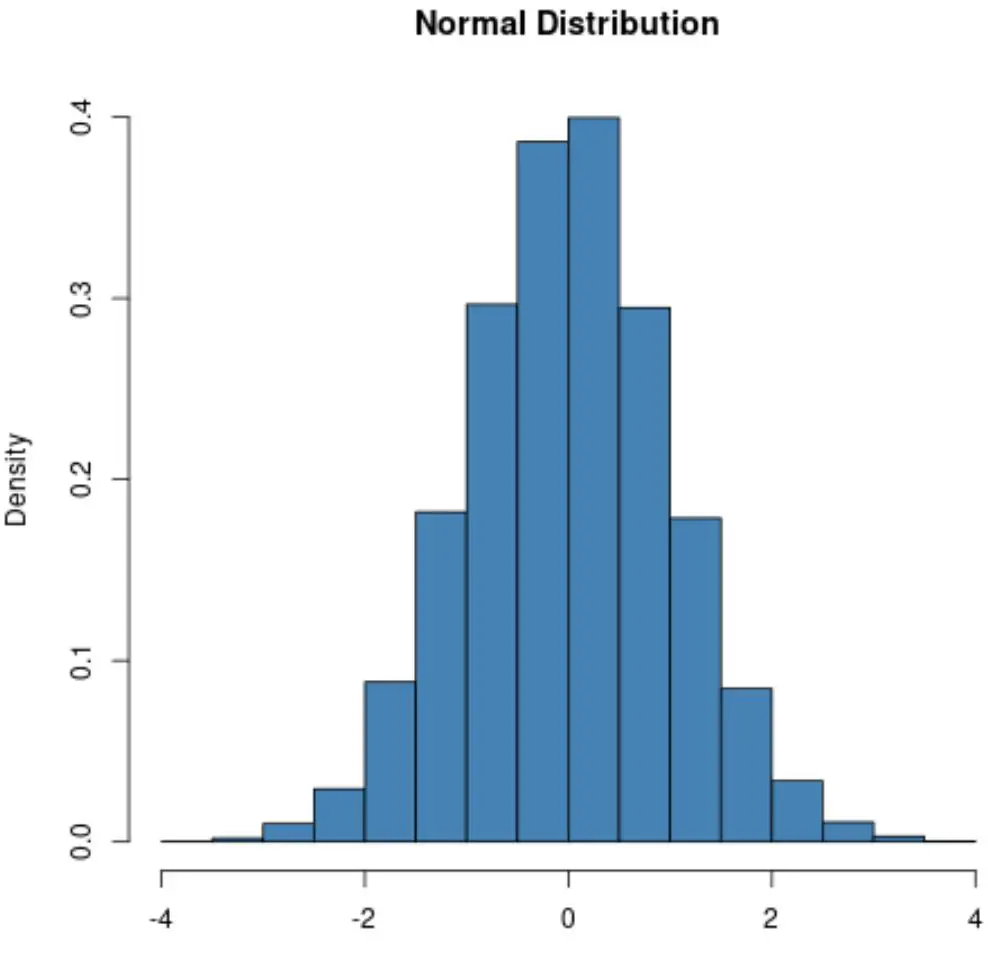
Однак форма розподілу Пуассона змінюється в залежності від середнього значення розподілу.
Наприклад, розподіл Пуассона з малим значенням для середнього, наприклад μ = 3, буде сильним правим перекосом :
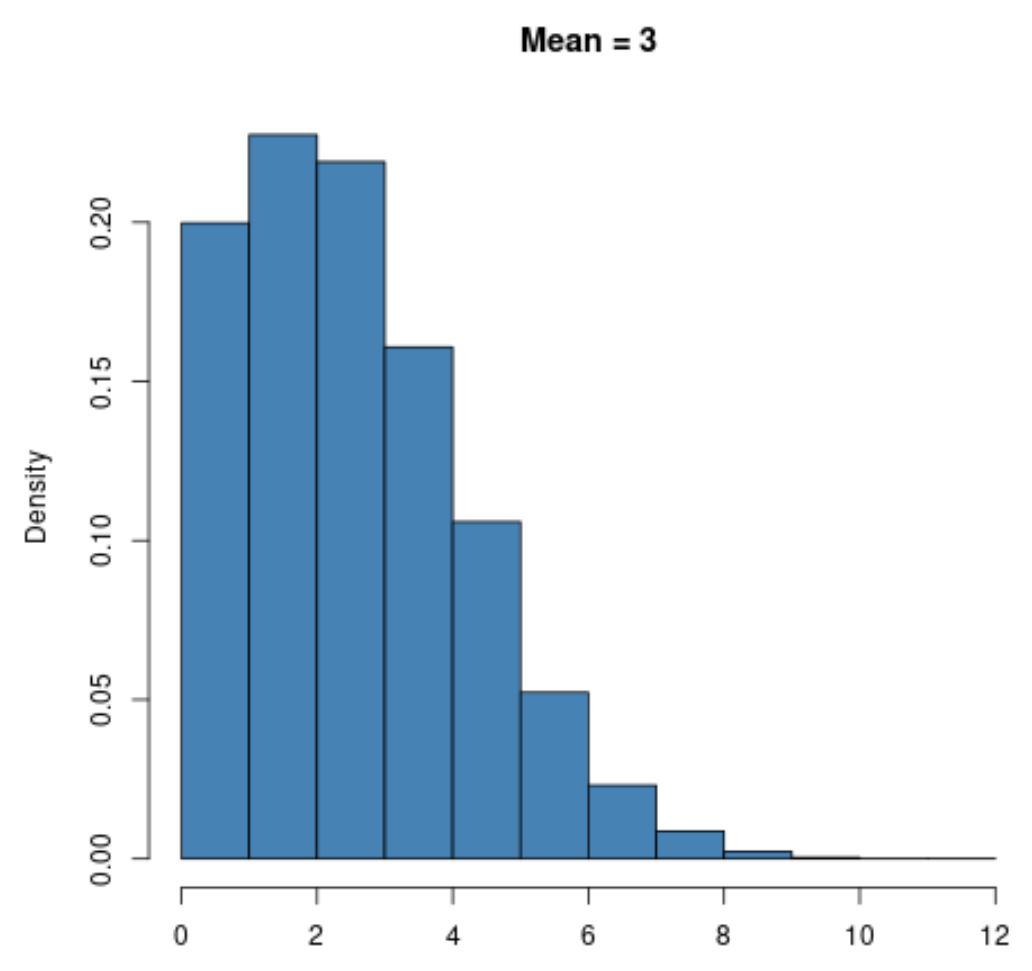
Однак розподіл Пуассона з більшим середнім значенням, таким як μ = 20 , матиме форму дзвона, як і звичайний розподіл:
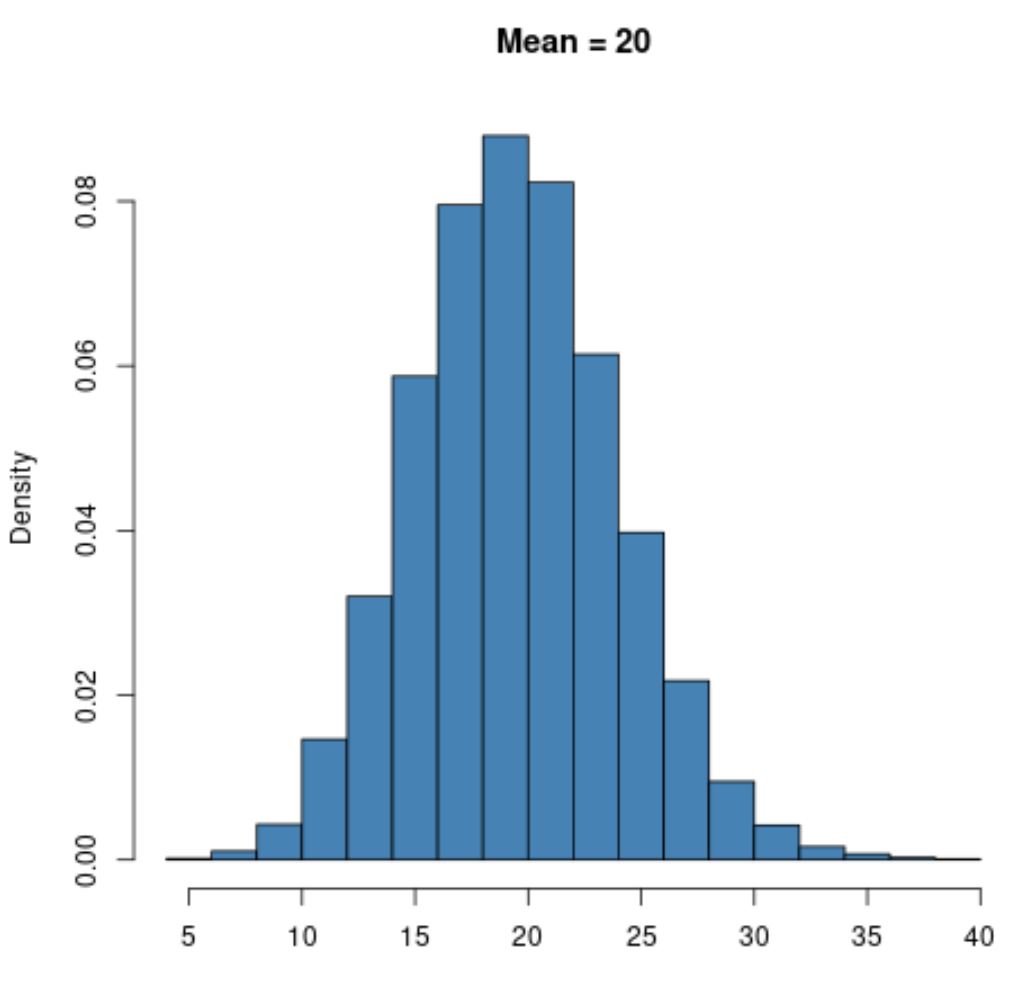
Зверніть увагу, що нижня межа розподілу Пуассона завжди буде дорівнювати нулю, незалежно від значення середнього, оскільки розподіл Пуассона можна використовувати лише з цілими значеннями, що дорівнюють або перевищують нуль.
Додаткові ресурси
У наступних посібниках надається додаткова інформація про розподіл Пуассона:
Введення в розподіл Пуассона
Чотири гіпотези розподілу Пуассона
5 конкретних прикладів розподілу Пуассона
Наступні посібники надають додаткову інформацію про нормальний розподіл:
Введення в нормальний розподіл
6 конкретних прикладів нормального розподілу
Генератор набору даних звичайного розподілу