Розподіл вейбулла

за Редакція 3 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке розподіл Вейбулла та для чого він використовується. Крім того, ви зможете побачити графічне представлення розподілу Вейбулла та властивості цього типу розподілу ймовірностей.

Що таке розподіл Вейбулла?

Розподіл Вейбулла — це безперервний розподіл ймовірностей, який визначається двома характерними параметрами: параметром форми α і параметром масштабу λ.

У статистиці розподіл Вейбулла в основному використовується для аналізу виживання. Подібним чином розподіл Вейбулла має багато застосувань у різних сферах. Нижче ми детально розглянемо використання розподілу Вейбулла.

$X\sim\text{Weibull}(\alpha,\lambda)$

На думку авторів, розподіл Вейбулла також можна параметризувати трьома параметрами. Потім додається третій параметр, який називається пороговим значенням, який вказує абсцису, на якій починається графік розподілу.

Розподіл Вейбулла названо на честь шведа Валодді Вейбулла, який детально описав його в 1951 році. Однак розподіл Вейбулла був відкритий Морісом Фреше в 1927 році та вперше застосований Розіном і Раммлером у 1933 році.

Побудова розподілу Вейбулла

Ознайомившись з визначенням розподілу Вейбулла, ми побачимо, як змінюється його графічне представлення в залежності від значень його параметрів.

Нижче ви можете побачити кілька прикладів того, як змінюється графік функції щільності розподілу Вейбулла в залежності від значення параметра форми та параметра масштабу.

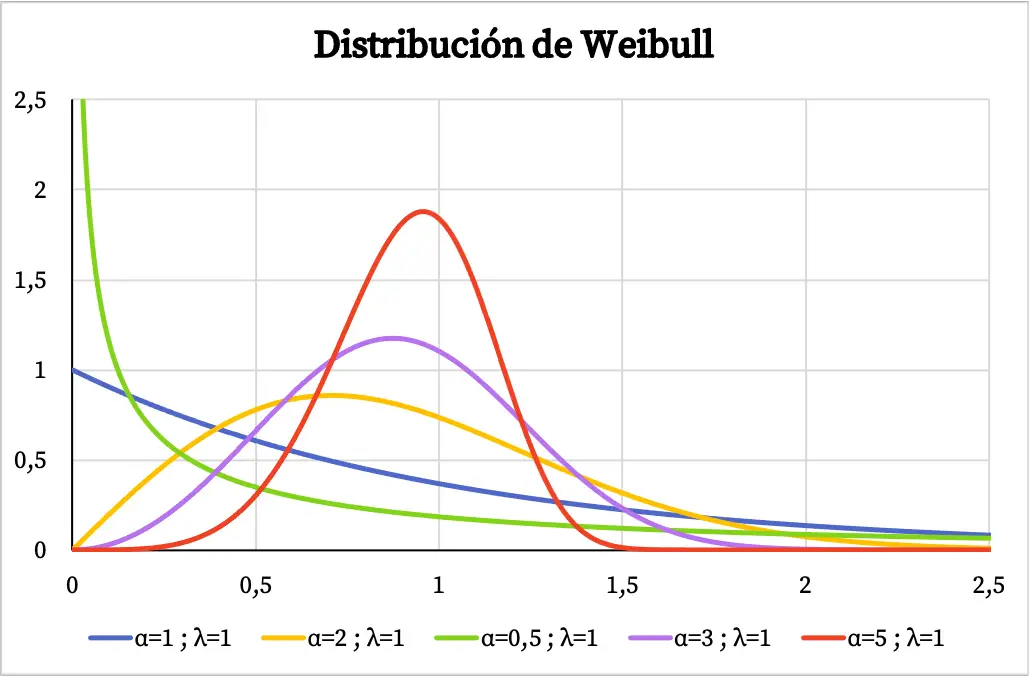
Коли розподіл Вейбулла використовується для моделювання інтенсивності відмов системи як функції часу, значення параметра форми α означає наступне:

α<1: частота відмов зменшується з часом.
α=1: частота відмов постійна протягом часу.
α>1: частота відмов зростає з часом.

З іншого боку, на наступному графіку ви можете побачити кумулятивну функцію ймовірності розподілу Вейбулла, побудовану на основі його характерних значень.

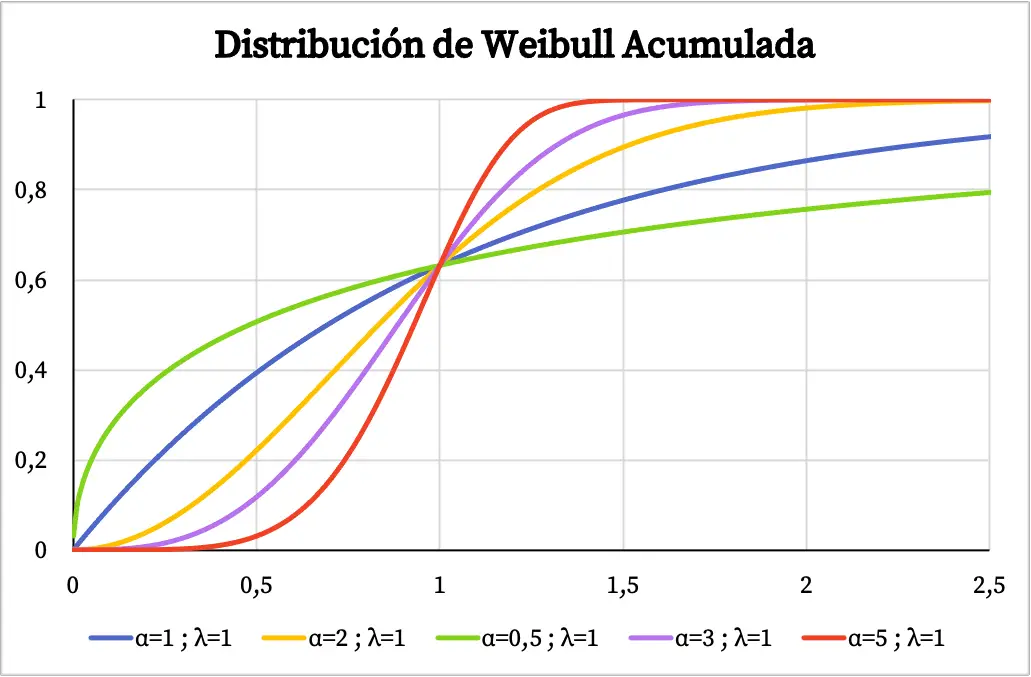
кумулятивна ймовірність розподілу Вейбулла

Характеристика розподілу Вейбулла

Розподіл Вейбулла має такі характеристики:

Розподіл Вейбулла має два характерних параметри, які визначають його графік: параметр форми α і параметр масштабу λ. Обидва параметри є додатними дійсними числами.

$\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=”Rendered by QuickLaTeX.com” height=”92″ width=”101″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Розподіл Вейбулла приймає лише позитивні значення абсцис.</li> </ul> <p class=$ $x\in (0,+\infty)$

Середнє значення розподілу Вейбулла обчислюється за такою формулою:

$\displaystyle E[X]=\frac{1}{\lambda}\;\Gamma\left(1+\frac{1}{\alpha}\right)$

З іншого боку, формула для знаходження дисперсії розподілу Вейбулла:

$\displaystyle Var(X)=\frac{1}{\lambda^2}\left[\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma^2\left(1+\frac{1}{\alpha}\right)\right]$

Мода випадкової величини, яка відповідає розподілу Вейбулла з α>1, може бути визначена таким виразом:

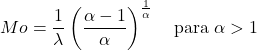
$\displaystyle Mo=\frac{1}{\lambda}\left(\frac{\alpha-1}{\alpha} \right)^{\frac{1}{\alpha}} \quad \text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”50″ width=”257″ style=”vertical-align: -17px;”></p> </p> <ul> <li> Формула для функції густини розподілу Вейбулла:</li> </ul> <p class=$ $\displaystyle P[X=x]=\lambda\alpha(\lambda x)^{\alpha-1}e^{-(\lambda x)^\alpha}$

Подібним чином формула для кумулятивної функції ймовірності розподілу Вейбулла має вигляд:

$\displaystyle P[X\leq x]=1- e^{-(\lambda x)^\alpha}$

Коефіцієнт асиметрії розподілу Вейбулла розраховується за такою формулою:

$\displaystyle A=\frac{\displaystyle\Gamma\left(1+\frac{3}{\alpha}\right)\frac{|}{\lambda^3}-3\mu\sigma^2-\mu^3}{\sigma^3}$

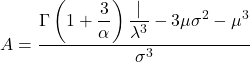
Нарешті, формула, яка дає змогу визначити коефіцієнт ексцесу розподілу Вейбулла, така:

$\displaystyle C=\frac{\displaystyle\frac{1}{\lambda^4}\Gamma \left(1+\frac{4}{\alpha}\right)-4\gamma_{1}\sigma^3\mu-6\mu^2\sigma^2-\mu^4}{\sigma^4}$

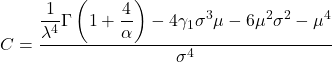
золото

$\Gamma_i=\Gamma\left(1+\frac{i}{\alpha}\right).$

Застосування розподілу Вейбулла

Розподіл Weibull має багато застосувань, зокрема:

У прикладній статистиці розподіл Вейбулла використовується в аналізі виживання.
У техніці розподіл Вейбулла використовується для моделювання функцій, пов’язаних із часом виготовлення.
У радіолокаційних системах для імітації дисперсії прийнятого сигналу.
У страховому секторі, щоб змоделювати розмір претензій.
У метеорології, наприклад, для моделювання частоти різних швидкостей вітру.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше