Розподіл вибірки

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке розподіл вибірки в статистиці та для чого він використовується. Отже, ви знайдете значення вибіркового розподілу, конкретний приклад вибіркового розподілу та, крім того, формули для найпоширеніших типів вибіркового розподілу.

Що таке розподіл вибірки?

Вибірковий розподіл або вибірковий розподіл — це розподіл, який є результатом розгляду всіх можливих вибірок сукупності. Іншими словами, вибірковий розподіл — це розподіл, отриманий шляхом обчислення параметра вибірки всіх можливих вибірок із сукупності.

Наприклад, якщо ми витягнемо всі можливі вибірки зі статистичної сукупності та обчислимо середнє значення кожної вибірки, набір вибіркових середніх утворить розподіл вибірки. Точніше, оскільки обчислений параметр є середнім арифметичним, він є вибірковим розподілом середнього.

У статистиці вибірковий розподіл використовується для обчислення ймовірності наближення до значення параметра сукупності при дослідженні однієї вибірки. Подібним чином розподіл вибірки дозволяє нам оцінити похибку вибірки для заданого розміру вибірки.

Приклад розподілу вибірки

Тепер, коли ми знаємо визначення розподілу вибірки, давайте розглянемо простий приклад, щоб повністю зрозуміти концепцію.

У ящик ми кладемо три кулі, на кожній з яких записане число від одного до трьох, так що одна кулька має номер 1, інша кулька — 2, а остання — 3. Для зразка розміром n = 2, розраховує ймовірності вибіркового розподілу середнього, якщо відібрано вибірки із заміною.

Зразки відбираються із заміщенням, тобто кулька, взята для відбору першого елемента зразка, повертається в коробку і може бути відібрана знову під час другого вилучення. Отже, всі можливі вибірки з сукупності:

1,1 1,2 1,3
2.1 2.2 2.3
3.1 3.2 3.3

Таким чином, обчислюємо середнє арифметичне кожної можливої вибірки:

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

Отже, ймовірності отримання кожного значення вибіркового середнього при відборі випадкової вибірки з сукупності наступні:

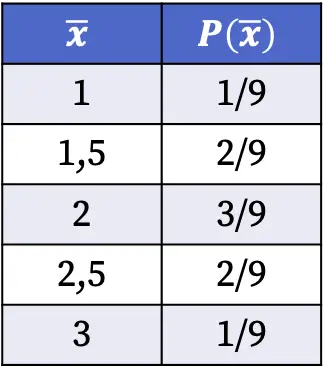
Імовірності розподілу вибірки, наведені в таблиці вище, були розраховані шляхом ділення кількості вибірок із вказаним середнім значенням на загальну кількість можливих випадків. Наприклад: середнє значення вибірки дорівнює 1,5 у двох випадках із дев’яти можливих, тому P(1,5)=2/9.

Види вибіркових розподілів

Вибіркові розподіли (або вибіркові розподіли) можна класифікувати на основі параметра вибірки, з якого вони були отримані. Отже, найпоширенішими типами розподілів є:

Вибірковий розподіл середнього : це вибірковий розподіл, який є результатом обчислення середнього арифметичного кожного зразка.
Пропорційний вибірковий розподіл : це вибірковий розподіл, отриманий шляхом обчислення частки всіх вибірок.
Вибірковий розподіл дисперсії : це вибірковий розподіл, який утворює набір усіх дисперсій у вибірці.
Різниця середніх вибіркового розподілу : це вибірковий розподіл, який є результатом обчислення різниці між середніми значеннями всіх можливих вибірок із двох різних сукупностей.
Різниця в пропорціях. Розподіл вибірки : це розподіл вибірки, отриманий шляхом віднімання всіх можливих пропорцій вибірки з двох сукупностей.

Кожен тип розподілу вибірки пояснюється більш детально нижче.

Вибірковий розподіл середнього

Дано генеральну сукупність, яка відповідає нормальному розподілу ймовірностей із середнім

$\mu$

і стандартне відхилення

$\sigma$

і витягуються зразки розміру

$n$

, вибірковий розподіл середнього також буде визначено нормальним розподілом, що має такі характеристики:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

золото

$\mu_{\overline{x}}$

є середнім значенням вибіркового розподілу середнього значення та

$\sigma_{\overline{x}}$

є його стандартним відхиленням. Крім того,

$\cfrac{\sigma}{\sqrt{n}}$

стандартна помилка розподілу вибірки.

Примітка. Якщо генеральна сукупність не відповідає нормальному розподілу, але розмір вибірки є великим (n>30), вибірковий розподіл середнього також можна наблизити до нормального розподілу вище за межею центральної теореми.

Отже, оскільки вибірковий розподіл середнього відповідає нормальному розподілу, формула для обчислення будь-якої ймовірності, пов’язаної з вибірковим середнім, має вигляд:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

золото:

$\overline{x}$

це зразок засобів.
$\mu$

Це середній показник населення.
$s$

стандартне відхилення сукупності.
$n$

це розмір вибірки.
$Z$

є змінною, визначеною стандартним нормальним розподілом N(0,1).

➤ Див.: Розв’язана вправа на вибірковий розподіл середнього значення

Вибірковий розподіл частки

Фактично, коли ми вивчаємо частку вибірки, ми аналізуємо випадки успіху. Таким чином, випадкова змінна в дослідженні відповідає біноміальному розподілу ймовірностей.

Відповідно до центральної граничної теореми, для великих розмірів (n>30) ми можемо наблизити біноміальний розподіл до нормального. Таким чином, вибірковий розподіл частки наближається до нормального розподілу з такими параметрами:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

золото

$p$

це ймовірність успіху і

$q$

це ймовірність невдачі

$q=1-p$

Примітка. Біноміальний розподіл можна наблизити до нормального, лише якщо

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”></p> <p> ,</p> <p class=$ $np\ge 5$

$nq\ge 5$

Отже, оскільки вибірковий розподіл частки можна наблизити до нормального розподілу, формула для обчислення будь-якої ймовірності, пов’язаної з часткою вибірки, має вигляд:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

золото:

$\widehat{p}$

є пропорцією зразка.
$p$

це частка населення.
$q$

ймовірність відмови популяції,

$q=1-p$

.
$n$

це розмір вибірки.
$Z$

є змінною, визначеною стандартним нормальним розподілом N(0,1).

➤ Див.: Розв’язана вправа на вибірковий розподіл пропорції

Вибірковий розподіл дисперсії

Вибірковий розподіл дисперсії визначається розподілом ймовірності хі-квадрат. Таким чином, формула для статистики вибіркового розподілу дисперсії :

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

золото:

$\chi^2$

є статистикою вибіркового розподілу дисперсії, яка слідує за розподілом хі-квадрат.
$n$

це розмір вибірки.
$s^2$

дисперсія вибірки.
$\sigma^2$

є дисперсія сукупності.

➤ Див.: Розв’язана вправа на вибірковий розподіл дисперсії

Вибірковий розподіл різниці середніх

Якщо розмір вибірки достатньо великий (n ₁ ≥30 і n ₂ ≥30), вибірковий розподіл середньої різниці відповідає нормальному розподілу. Точніше, параметри зазначеного розподілу розраховуються наступним чином:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Примітка. Якщо обидві генеральні сукупності є нормальними розподілами, тоді вибірковий розподіл різниці середніх відповідає нормальному розподілу незалежно від розмірів вибірки.

Отже, оскільки вибірковий розподіл різниці середніх визначається нормальним розподілом, формула для розрахунку статистики вибіркового розподілу різниці середніх має вигляд:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

золото:

$\overline{x_i}$

є середнім значенням вибірки i.
$\mu_i$

це середнє значення населення i.
$\sigma_i$

є стандартним відхиленням сукупності i.
$n_i$

це розмір вибірки i.
$Z$

є змінною, визначеною стандартним нормальним розподілом N(0,1).

Зауважте, що вибірки з різних сукупностей можуть мати різні розміри вибірки.

➤ Див.: Розв’язана вправа на вибірковий розподіл різниці середніх

Вибірковий розподіл різниці в пропорціях

Вибірки, відібрані для розподілу вибірки різниць у пропорціях, визначаються біноміальними розподілами, оскільки для практичних цілей пропорція є відношенням успішних випадків до загальної кількості спостережень.

Однак завдяки центральній граничній теоремі біноміальні розподіли можуть бути наближені до нормальних розподілів ймовірностей. Таким чином, вибірковий розподіл різниці в пропорціях може бути наближено до нормального розподілу з такими характеристиками:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Примітка. Вибірковий розподіл різниці в пропорціях можна наблизити до нормального розподілу, лише якщо

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

$n_2q_2\geq5$

Отже, оскільки вибірковий розподіл різниці в пропорціях можна наблизити до нормального розподілу, формула для розрахунку статистики вибіркового розподілу різниці в пропорціях виглядає наступним чином:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

золото:

$\widehat{p_i}$

є пропорцією зразка i.
$p_i$

це частка населення i.
$q_i$

ймовірність відмови популяції i,

$q_i=1-p_i$

.
$n_i$

це розмір вибірки i.
$Z$

є змінною, визначеною стандартним нормальним розподілом N(0,1).

➤ Дивіться: Розв’язана вправа на вибірковий розподіл різниці пропорцій

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке розподіл вибірки?

Приклад розподілу вибірки

Види вибіркових розподілів

Вибірковий розподіл середнього

Вибірковий розподіл частки

Вибірковий розподіл дисперсії

Вибірковий розподіл різниці середніх

Вибірковий розподіл різниці в пропорціях

Про автора

Редакція

Додати коментар