Як обчислити розподіл вибірки в excel

Вибірковий розподіл — це розподіл імовірностей певної статистики на основі багатьох випадкових вибірок з однієї сукупності .

У цьому підручнику пояснюється, як виконати такі дії за допомогою розподілів вибірки в Excel:

• Створіть розподіл вибірки.
• Візуалізуйте розподіл вибірки.
• Обчисліть середнє значення та стандартне відхилення розподілу вибірки.
• Обчисліть ймовірності щодо розподілу вибірки.

Створіть розподіл вибірки в Excel

Припустімо, ми хочемо створити розподіл вибірки, що складається з 1000 вибірок, у яких розмір кожної вибірки дорівнює 20 і походить від нормального розподілу із середнім значенням 5,3 і стандартним відхиленням 9 .

Ми можемо легко зробити це, ввівши таку формулу в клітинку A2 нашої електронної таблиці:

 = NORM . INV ( RAND (), 5.3, 9)

Потім ми можемо навести курсор на правий нижній кут клітинки, доки не з’явиться маленький + , і перетягнути формулу на 20 клітинок праворуч і вниз на 1000 клітинок:

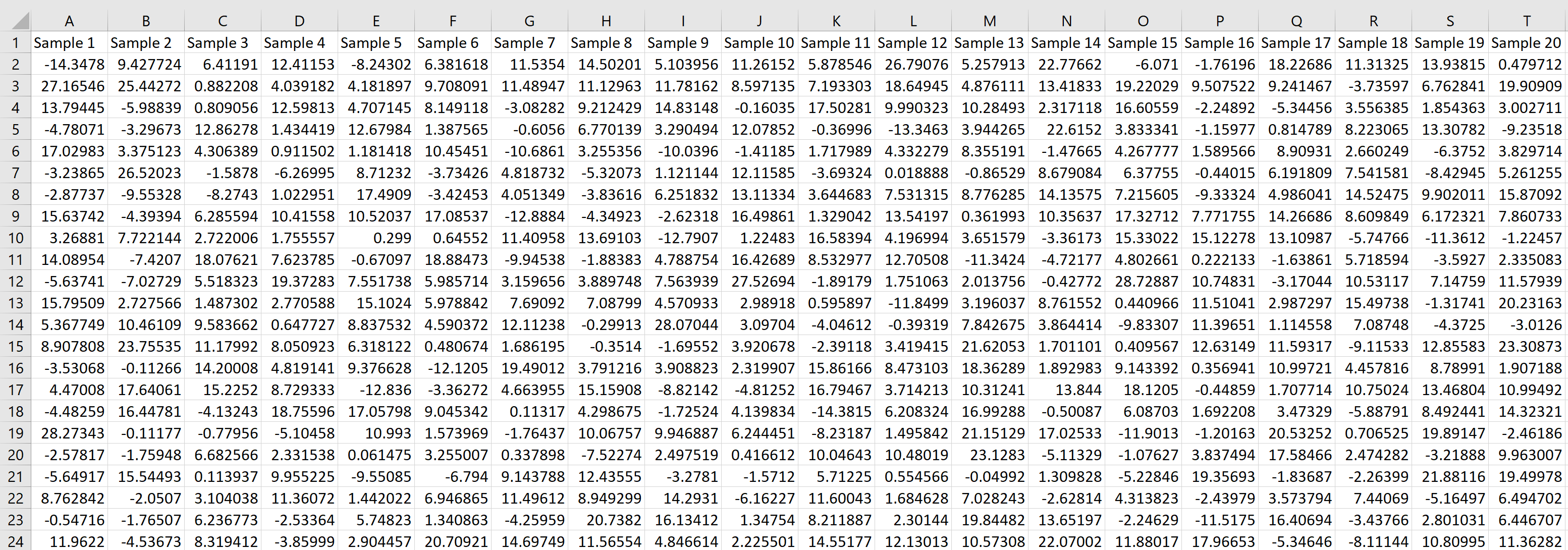
Кожен рядок представляє вибірку розміром 20, у якій кожне значення походить від нормального розподілу із середнім значенням 5,3 і стандартним відхиленням 9.

Знайдіть середнє значення та стандартне відхилення

Щоб знайти середнє значення та стандартне відхилення цього вибіркового розподілу вибіркових середніх, ми можемо спочатку знайти середнє значення кожної вибірки, ввівши таку формулу в комірку U2 нашого аркуша:

 = AVERAGE (A2:T2)

Потім ми можемо навести курсор на нижній правий кут клітинки, доки не з’явиться маленький + , і двічі клацнути цю формулу, щоб скопіювати цю формулу в усі інші клітинки в стовпці U:

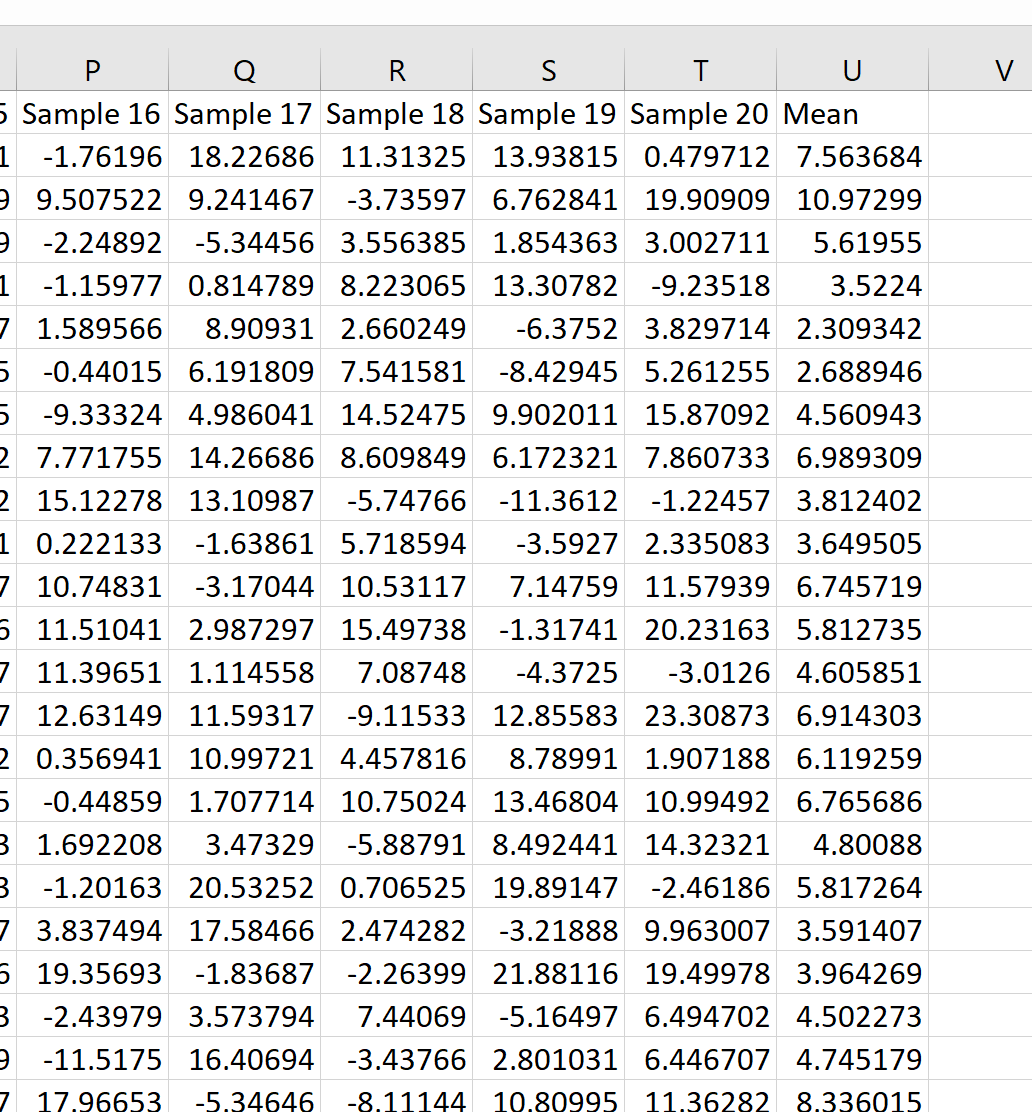
Ми бачимо, що перша вибірка мала середнє значення 7,563684, друга вибірка мала середнє значення 10,97299 і так далі.

Потім ми можемо використати наступні формули для обчислення середнього значення та стандартного відхилення вибіркових середніх:

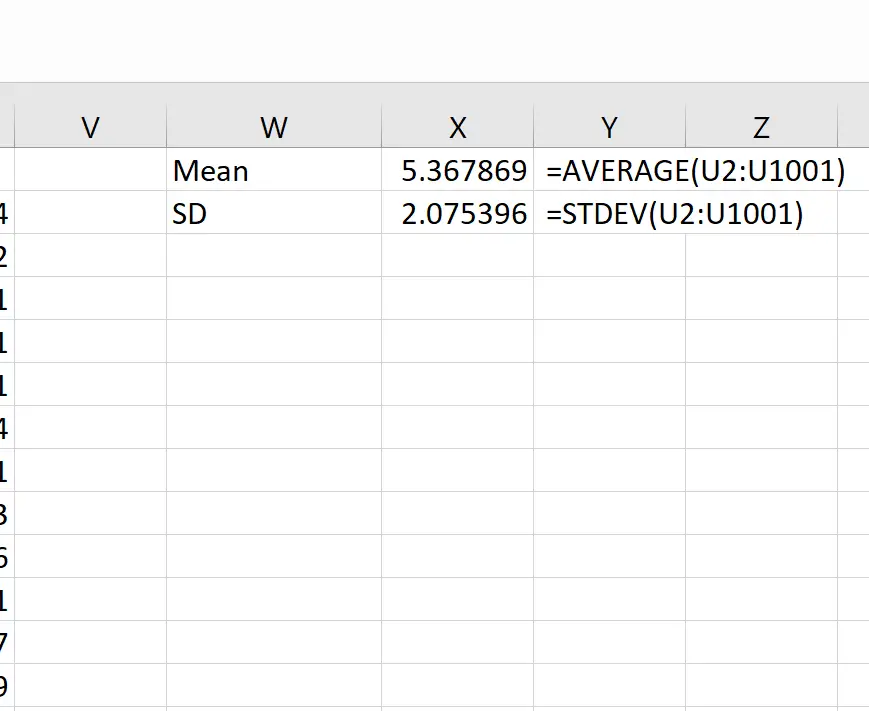
Теоретично, середнє значення вибіркового розподілу повинно бути 5,3. Ми бачимо, що фактичне середнє значення вибірки в цьому прикладі становить 5,367869 , що близько до 5,3.

І теоретично, стандартне відхилення розподілу вибірки має дорівнювати s/√n, що буде 9 / √20 = 2,012. Ми бачимо, що фактичне стандартне відхилення розподілу вибірки становить 2,075396 , що близько до 2,012.

Візуалізуйте розподіл вибірки

Ми також можемо створити просту гістограму для візуалізації розподілу вибіркових середніх значень.

Для цього просто виділіть усі вибіркові середні у стовпці U, клацніть вкладку «Вставити» , а потім клацніть параметр «Гістограма» в розділі «Діаграми» .

Це дає таку гістограму:

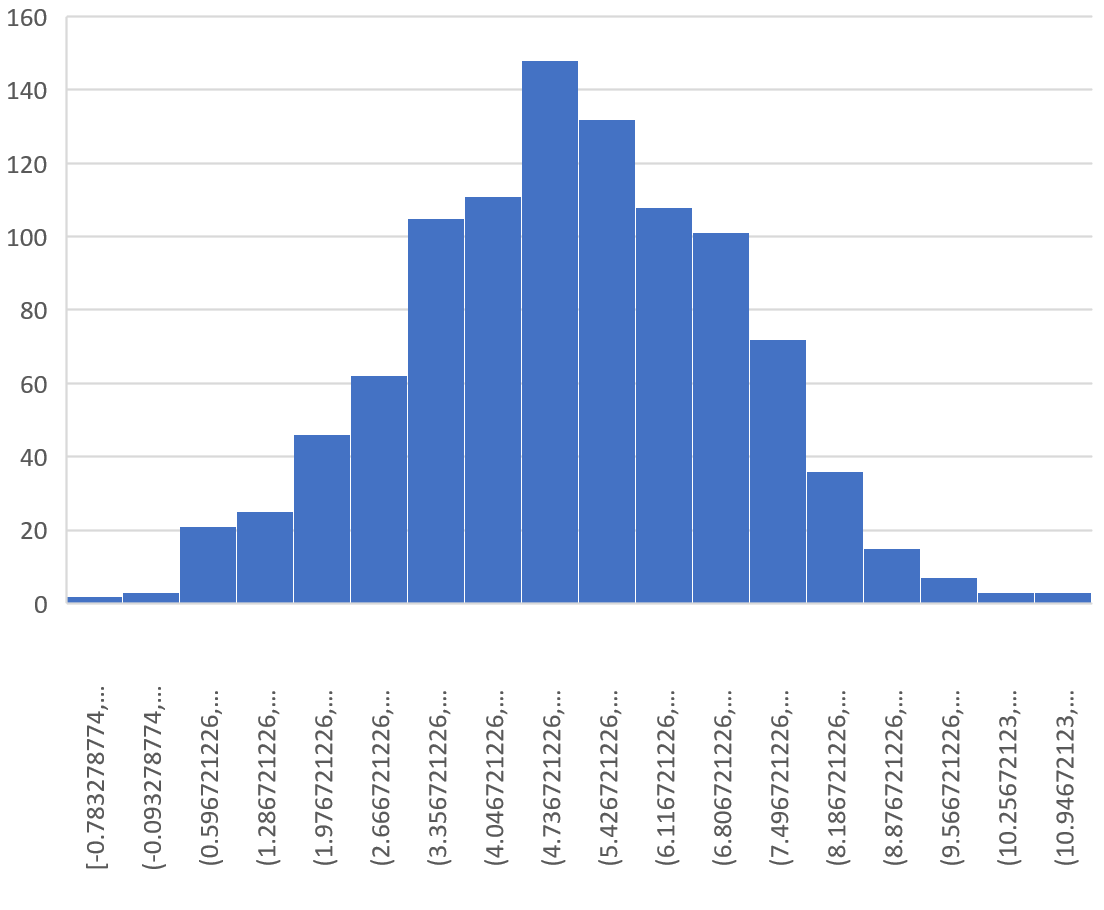
Можна побачити, що розподіл вибірки має дзвоноподібну форму з піком біля значення 5.

Однак із хвостів розподілу ми бачимо, що деякі зразки мали середнє значення більше 10, а інші мали значення менше 0.

Обчислити ймовірності

Ми також можемо обчислити ймовірність отримання певного значення для середнього вибіркового значення на основі середнього значення сукупності, стандартного відхилення сукупності та розміру вибірки.

Наприклад, ми можемо використати наступну формулу, щоб знайти ймовірність того, що середнє значення вибірки менше або дорівнює 6, враховуючи, що середнє значення генеральної сукупності становить 5,3, стандартне відхилення генеральної сукупності становить 9, а розмір вибірки становить:

 = COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)

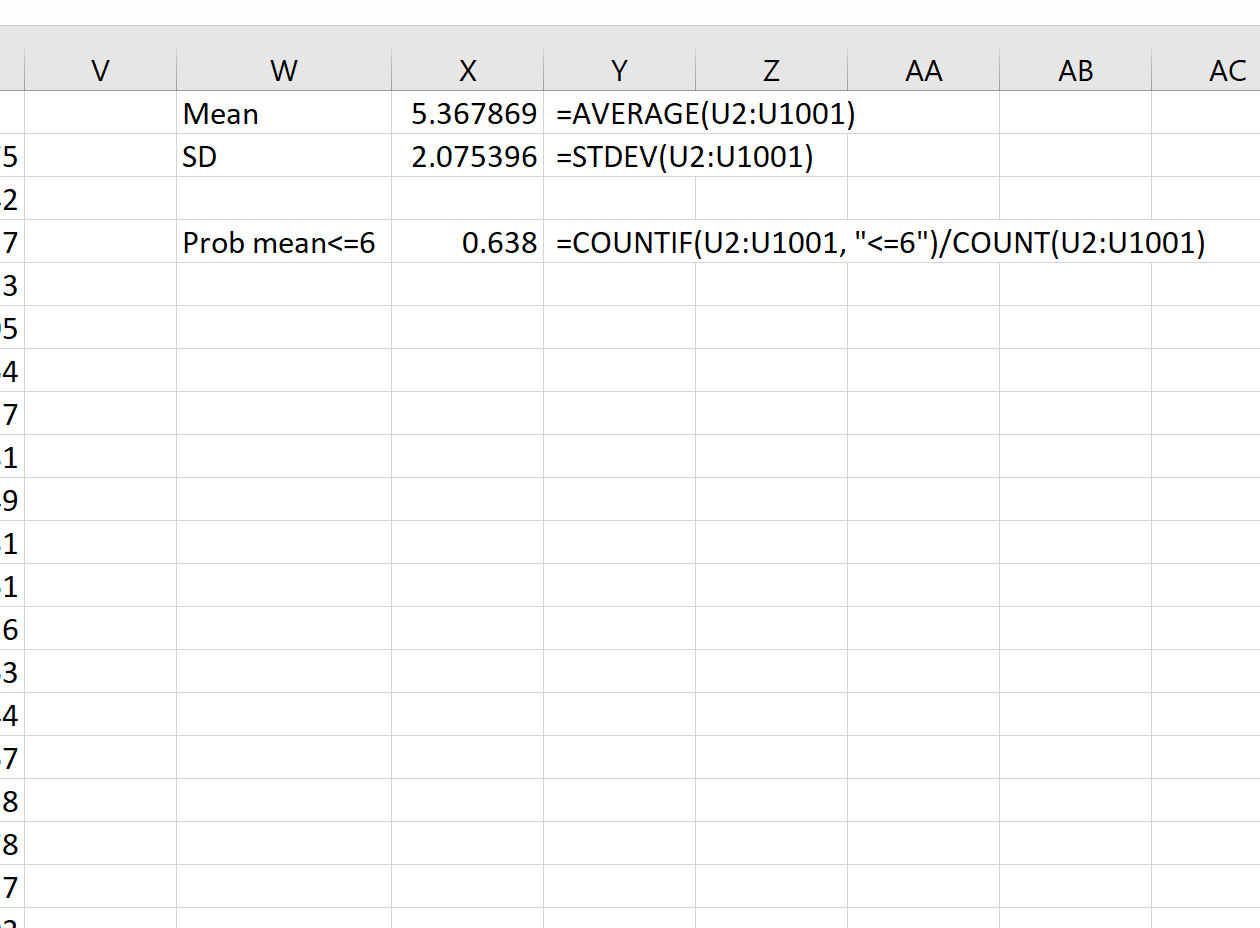
Ми бачимо, що ймовірність того, що вибіркове середнє менше або дорівнює 6, становить 0,638.

Це дуже близько до ймовірності, обчисленої калькулятором розподілу вибірки :

Додаткові ресурси

Вступ до розподілу вибірки
Калькулятор розподілу вибірки
Вступ до центральної граничної теореми