Як обчислити розподіл вибірки в r
Вибірковий розподіл — це розподіл ймовірностей певної статистики на основі багатьох випадкових вибірок з однієї сукупності.
Цей підручник пояснює, як зробити наступне з розподілами вибірки в R:
- Створіть розподіл вибірки.
- Візуалізуйте розподіл вибірки.
- Обчисліть середнє значення та стандартне відхилення розподілу вибірки.
- Обчисліть ймовірності щодо розподілу вибірки.
Створіть розподіл вибірки в R
Наступний код показує, як створити розподіл вибірки в R:
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656
У цьому прикладі ми використали функцію rnorm() , щоб обчислити середнє значення 10 000 вибірок, у яких розмір кожної вибірки становив 20 і був згенерований із нормального розподілу із середнім значенням 5,3 і стандартним відхиленням 9.
Ми бачимо, що перша вибірка мала середнє значення 5,283992, друга вибірка мала середнє значення 6,304845 і так далі.
Візуалізуйте розподіл вибірки
Наступний код показує, як створити просту гістограму для візуалізації розподілу вибірки:
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")
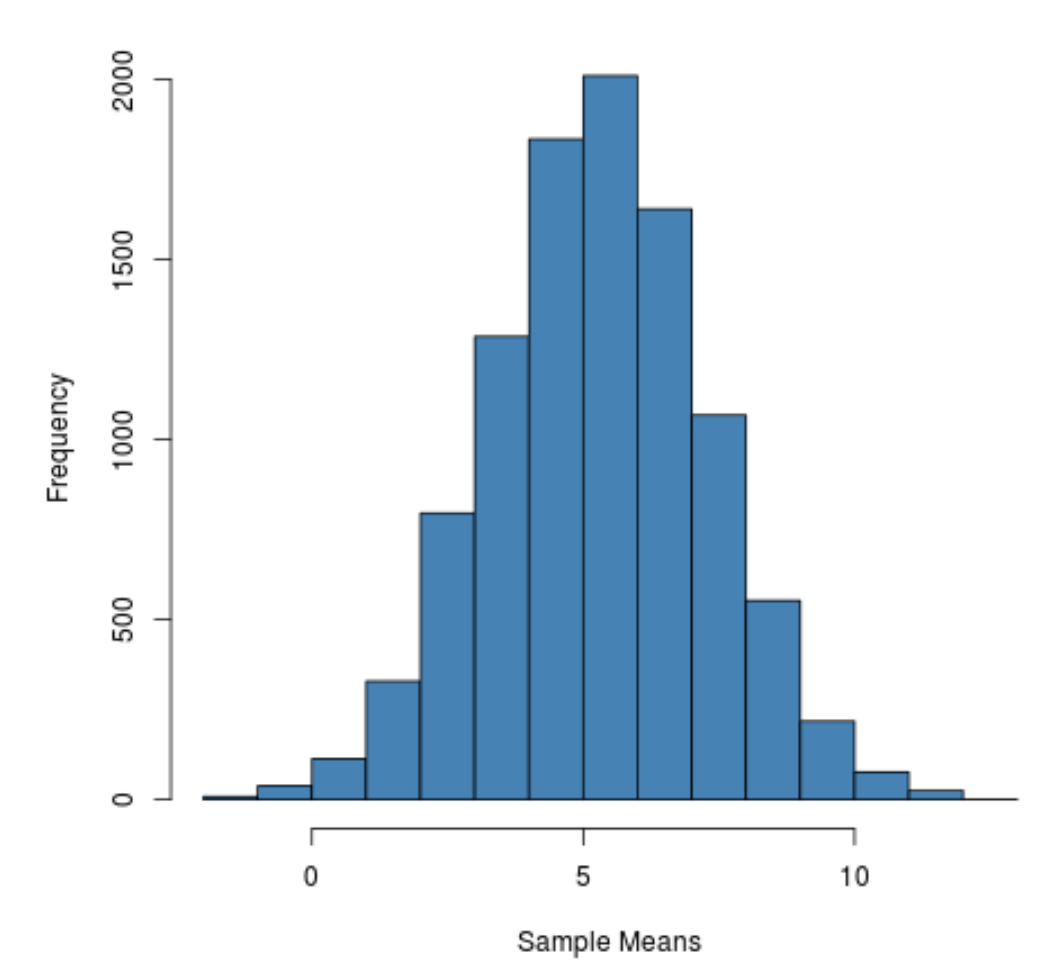
Можна побачити, що розподіл вибірки має дзвоноподібну форму з піком біля значення 5.
Однак із хвостів розподілу ми бачимо, що деякі зразки мали середнє значення більше 10, а інші мали значення менше 0.
Знайдіть середнє значення та стандартне відхилення
У наступному коді показано, як обчислити середнє значення та стандартне відхилення розподілу вибірки:
#mean of sampling distribution
mean(sample_means)
[1] 5.287195
#standard deviation of sampling distribution
sd(sample_means)
[1] 2.00224
Теоретично, середнє значення вибіркового розподілу повинно бути 5,3. Ми бачимо, що фактичне середнє значення вибірки в цьому прикладі становить 5,287195 , що близько до 5,3.
І теоретично, стандартне відхилення розподілу вибірки має дорівнювати s/√n, що буде 9 / √20 = 2,012. Ми бачимо, що фактичне стандартне відхилення розподілу вибірки становить 2,00224 , що близько до 2,012.
Обчислити ймовірності
У наступному коді показано, як обчислити ймовірність отримання певного значення для вибіркового середнього, враховуючи середнє значення сукупності, стандартне відхилення сукупності та розмір вибірки.
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
У цьому конкретному прикладі ми знаходимо ймовірність того, що середнє значення вибірки менше або дорівнює 6, враховуючи, що середнє значення сукупності становить 5,3, стандартне відхилення сукупності становить 9, а розмір вибірки з 20 становить 0,6417 .
Це дуже близько до ймовірності, обчисленої калькулятором розподілу вибірки :

Повний код
Повний код R, використаний у цьому прикладі, наведено нижче:
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")
#mean of sampling distribution
mean(sample_means)
#standard deviation of sampling distribution
sd(sample_means)
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
Додаткові ресурси
Вступ до розподілу вибірки
Калькулятор розподілу вибірки
Вступ до центральної граничної теореми