Вибірковий розподіл частки
У цій статті пояснюється, що таке вибірковий розподіл частки в статистиці. Так само ви знайдете формулу розподілу пропорційної вибірки та, крім того, покрокову вправу.
Який вибірковий розподіл частки?
Вибірковий розподіл пропорцій (або вибірковий розподіл пропорцій ) — це розподіл, який є результатом обчислення частки кожної можливої вибірки із сукупності. Тобто пропорції вибірки всіх можливих вибірок із генеральної сукупності утворюють розподіл вибірки пропорції.
Іншими словами, пропорційний розподіл вибірки виходить шляхом вивчення всіх вибірок, які можна відібрати з генеральної сукупності, і визначення частки вибірки для кожної вибірки. Таким чином, набір обчислених пропорцій вибірки становить вибірковий розподіл пропорції.
Якщо вам цікаво, для чого призначений вибірковий розподіл пропорції, у статистиці він використовується для обчислення ймовірності наближення до значення пропорції генеральної сукупності під час аналізу однієї вибірки.
Формула розподілу пропорційної вибірки
Фактично, коли ми вивчаємо частку вибірки, ми аналізуємо випадки успіху. Таким чином, випадкова змінна в дослідженні відповідає біноміальному розподілу ймовірностей .
Відповідно до центральної граничної теореми, для великих розмірів (n>30) ми можемо наблизити біноміальний розподіл до нормального. Таким чином, вибірковий розподіл частки наближається до нормального розподілу з такими параметрами:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f3408076893f390bb65baecfe38e6eff_l3.png)
золото
![]()
це ймовірність успіху і
![]()
це ймовірність невдачі
![]()
.
Примітка. Біноміальний розподіл можна наблизити до нормального, лише якщо

![]()
І
![]()
.
Отже, оскільки вибірковий розподіл частки можна наблизити до нормального розподілу, формула для розрахунку будь-якої ймовірності, пов’язаної з часткою вибірки, має вигляд:

золото:
-

є пропорцією зразка.
-

це частка населення.
-

ймовірність відмови популяції,

.
-

це розмір вибірки.
-

є змінною, визначеною стандартним нормальним розподілом N(0,1).
Конкретний приклад пропорційного розподілу вибірки
Після того, як ми ознайомилися з визначенням пропорційного вибіркового розподілу та пов’язаними з ним формулами, нижче наведено покроковий приклад вирішення, щоб повністю зрозуміти концепцію.
- Промислова компанія купує партії деталей на заводі, який стверджує, що виробляє деталі лише з 3% бракованих деталей. Щоб перевірити це, компанія вирішує проаналізувати замовлення з 500 деталей. Яка ймовірність виявлення у зразку більше 5% бракованих деталей?
У цьому випадку частка населення, яку ми хочемо вивчити, становить 0,03, тому параметр q еквівалентний 0,97.
![Rendered by QuickLaTeX.com \begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f4354c268853ec7b592bcacd23f3b214_l3.png)
Отже, щоб знайти ймовірність того, що вони запитують нас, ми повинні обчислити відповідну статистику, застосувавши формулу, яку ми бачили в попередньому розділі:
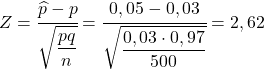
Таким чином, ймовірність отримати більше 5% бракованих деталей еквівалентна такій ймовірності:
![P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”360″ style=”vertical-align: -5px;”></p>
</p>
<p> Нарешті, ми шукаємо ймовірність P[Z≤2,62] у <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-a5e5cff61f2cc97762df561b3e35a7ba_l3.png) таблиці Z-розподілу та обчислюємо ймовірність, яку запитує нас задача:
таблиці Z-розподілу та обчислюємо ймовірність, яку запитує нас задача:
![\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}” title=”Rendered by QuickLaTeX.com” height=”167″ width=”162″ style=”vertical-align: 0px;”></p>
</p>
<p> Підсумовуючи, ймовірність виявлення більше 5% дефектних деталей в аналізованому зразку становить 0,44%.</p>
</div><!-- End Content -->
<!-- Start Author Box -->
<div class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-812f9b97c53e15da88b0cb7149f254c6_l3.png)
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше