Розподіл стьюдента

за 4 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке t-розподіл Стьюдента та для чого він використовується. Додатково показано графік t-розподілу Стьюдента та характеристики цього типу розподілу ймовірностей.

Що таке розподіл Стьюдента?

Розподіл Стьюдента — це розподіл ймовірностей, який широко використовується в статистиці. Зокрема, t-розподіл Стьюдента використовується в t-критерії Стьюдента для визначення різниці між середніми значеннями двох вибірок і встановлення довірчих інтервалів.

Розподіл Стьюдента був розроблений статистиком Вільямом Сілі Госсетом у 1908 році під псевдонімом «Студент».

Розподіл t Стьюдента визначається числом ступенів свободи, отриманим шляхом віднімання однієї одиниці із загальної кількості спостережень. Тому формула для визначення ступенів свободи t-розподілу Стьюдента має вигляд ν=n-1 .

\begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}

Графік розподілу t Стьюдента

Тепер, коли ми знаємо визначення t-розподілу Стьюдента, давайте подивимося, що таке його графік. Отже, нижче ви можете графічно побачити кілька прикладів t-розподілу Стьюдента з різними ступенями свободи.

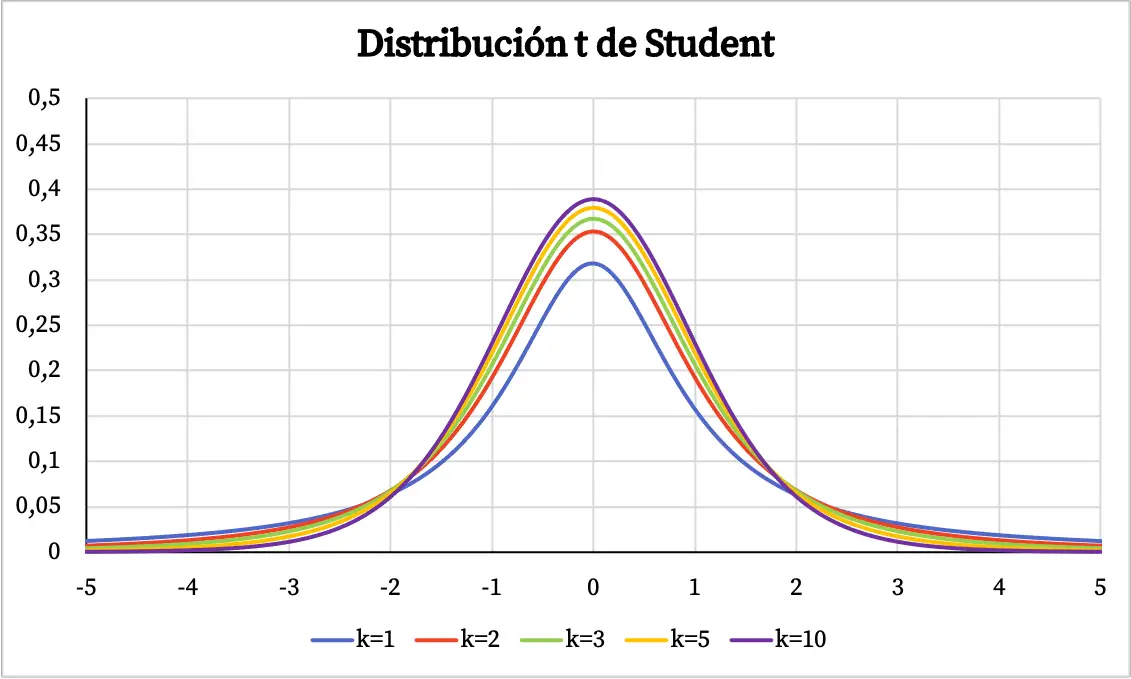
Графік розподілу t Стьюдента

З графіка t-розподілу Стьюдента можна вивести такі властивості:

  • Розподіл Стьюдента t є симетричним з центром у 0 і має форму дзвона.
  • Розподіл t Стьюдента є більш дисперсним, ніж нормальний розподіл, тобто крива розподілу t Стьюдента ширша.
  • Чим більше ступенів свободи має t-розподіл Стьюдента, тим менша його дисперсія.

На графіку вище функція щільності t-розподілу Стьюдента нанесена на графік залежно від його ступенів свободи. Однак нижче ви можете побачити, як змінюється кумулятивна функція ймовірності t-розподілу Стьюдента:

графік кумулятивного t-розподілу Стьюдента

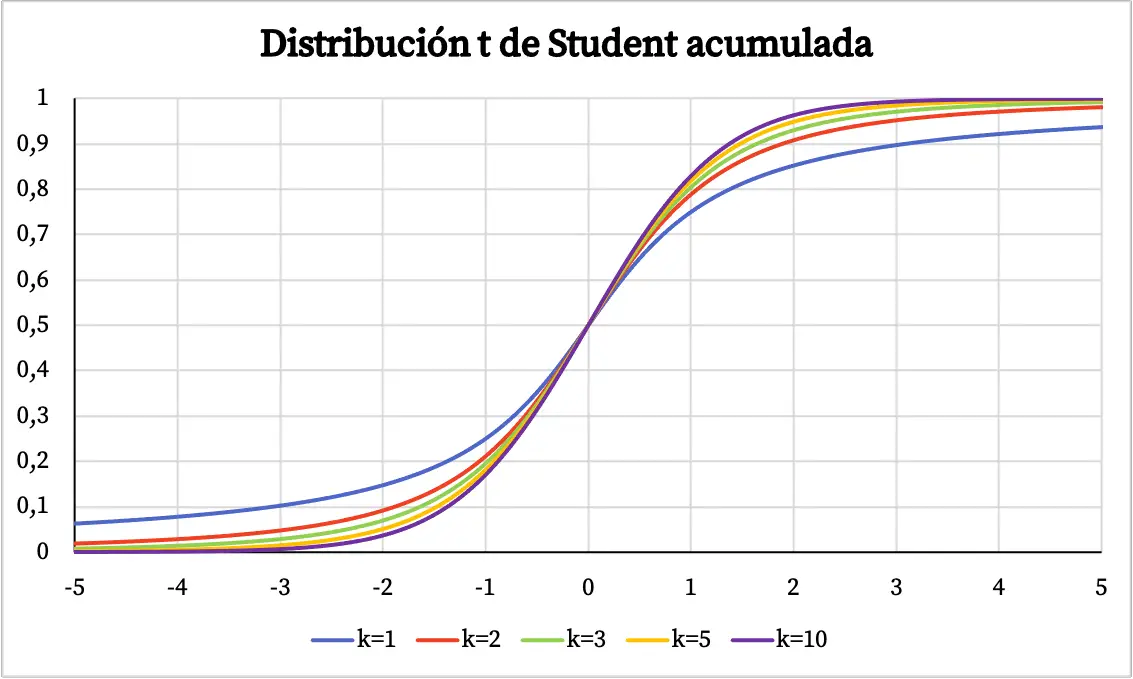
Характеристики t-розподілу Стьюдента

Найважливіші характеристики t-розподілу Стьюдента наведено нижче.

  • Область t-розподілу Стьюдента складається з дійсних чисел.

x\in (-\infty, +\infty)

  • Для t-розподілів Стьюдента з більш ніж одним ступенем свободи середнє значення розподілу дорівнює 0.

\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} ” title=”Rendered by QuickLaTeX.com” height=”55″ width=”190″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Дисперсію t-розподілу Стьюдента можна обчислити за допомогою такого виразу:</li> </ul> <p class=\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”245″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Медіана і мода t розподілу Стьюдента, незалежно від кількості ступенів свободи, завжди дорівнюють 0.</li> </ul> <p class=\begin{array}{c}Me=0\\[2ex]Mo=0\end{array}

  • Функція щільності t-розподілу Стьюдента визначається такою формулою:

\displaystyle P[X=x]=\frac{\Gamma((\nu+1)/2)} {\sqrt{\nu\pi}\,\Gamma(\nu/2)} (1+x^2/\nu)^{-(\nu+1)/2}

  • Кумулятивна функція розподілу ймовірностей t-розподілу Стьюдента визначається наступною формулою:

\displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}

  • Для t-розподілів Стьюдента зі ступенями свободи, більшими за 3, коефіцієнт асиметрії дорівнює нулю, оскільки це симетричний розподіл.

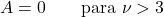
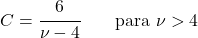\displaystyle A=0\qquad \text{para }\nu>3″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”164″ style=”vertical-align: -4px;”></p> </p> <ul> <li> Якщо ступені свободи t-розподілу Стьюдента більші за чотири, ексцес можна обчислити, поділивши шість на ступені свободи мінус чотири. </li> </ul> <p class=\displaystyle C=\cfrac{6}{\nu-4}\qquad \text{para }\nu>4″ title=”Rendered by QuickLaTeX.com” height=”38″ width=”198″ style=”vertical-align: -12px;”></p> </p> <h2 class= Застосування t-розподілу Стьюдента

Розподіл Стьюдента — це розподіл ймовірностей, який широко використовується в статистиці. Насправді існує навіть t-критерій Стьюдента, який використовується для перевірки гіпотез і довірчих інтервалів.

Таким чином, t-розподіл Стьюдента дозволяє нам проаналізувати різницю між середніми значеннями двох вибірок, точніше, він використовується для визначення того, чи дві вибірки мають суттєво різні середні значення. Подібним чином критерій Стьюдента використовується, щоб дізнатися, чи має лінія, отримана в результаті аналізу лінійної регресії, нахил чи ні.

Коротше кажучи, застосування t-розподілу Стьюдента покладається на аналіз наборів даних, які теоретично відповідають нормальному розподілу, але загальна кількість спостережень надто мала, щоб використовувати цей тип розподілу.

Про автора

Доктор Бенджамін Андерсон
Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Додати коментар

Ваша e-mail адреса не оприлюднюватиметься. Обов’язкові поля позначені *