Snedecor f розповсюдження
У цій статті пояснюється, що таке дистрибутив Snedecor F і для чого він використовується. Крім того, ви зможете побачити графік розподілу Snedecor F і його статистичні властивості.
Що таке розподіл Snedecor F?
F-розподіл Снедекора , також званий F-розподілом Фішера–Снедекора або просто F-розподілом , є безперервним розподілом ймовірностей, який використовується в статистичному висновку, зокрема в дисперсійному аналізі.
Однією з властивостей F-розподілу Снедекора є те, що він визначається значенням двох дійсних параметрів, m і n , які вказують їхні ступені свободи. Таким чином, символом для розподілу Снедекора F є F m,n , де m і n є параметрами, які визначають розподіл.

![Rendered by QuickLaTeX.com \left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d407869e61ca4357ffbcb40df3bd83ab_l3.png)
Розподіл Фішера-Снедекора F отримав свою назву на честь англійського статистика Рональда Фішера та американського статистика Джорджа Снедекора.
У статистиці F-розподіл Фішера-Снедекора має різні застосування. Наприклад, F-розподіл Фішера-Снедекора використовується для порівняння різних моделей лінійної регресії, а цей розподіл ймовірностей використовується в дисперсійному аналізі (ANOVA).
Діаграма розподілу Snedecor F
Після того, як ми побачили визначення F-розподілу Снедекора, нижче наведено графік його функції щільності та графік його кумулятивної ймовірності.
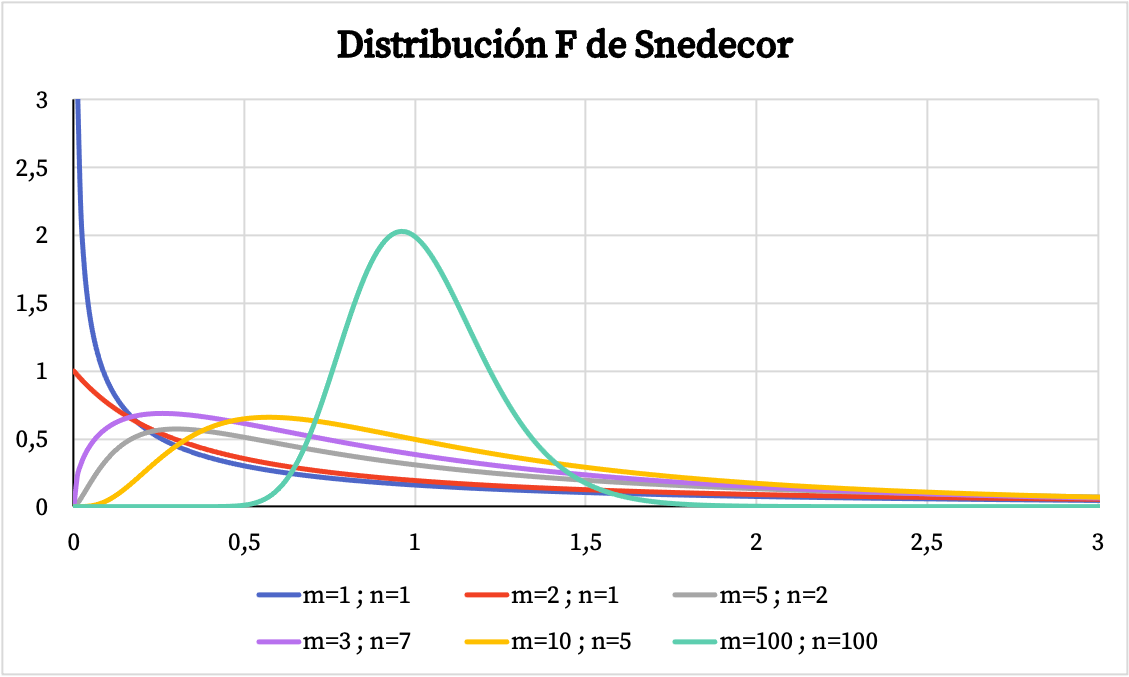
На графіку нижче ви можете побачити кілька прикладів розподілів Snedecor F з різними ступенями свободи.
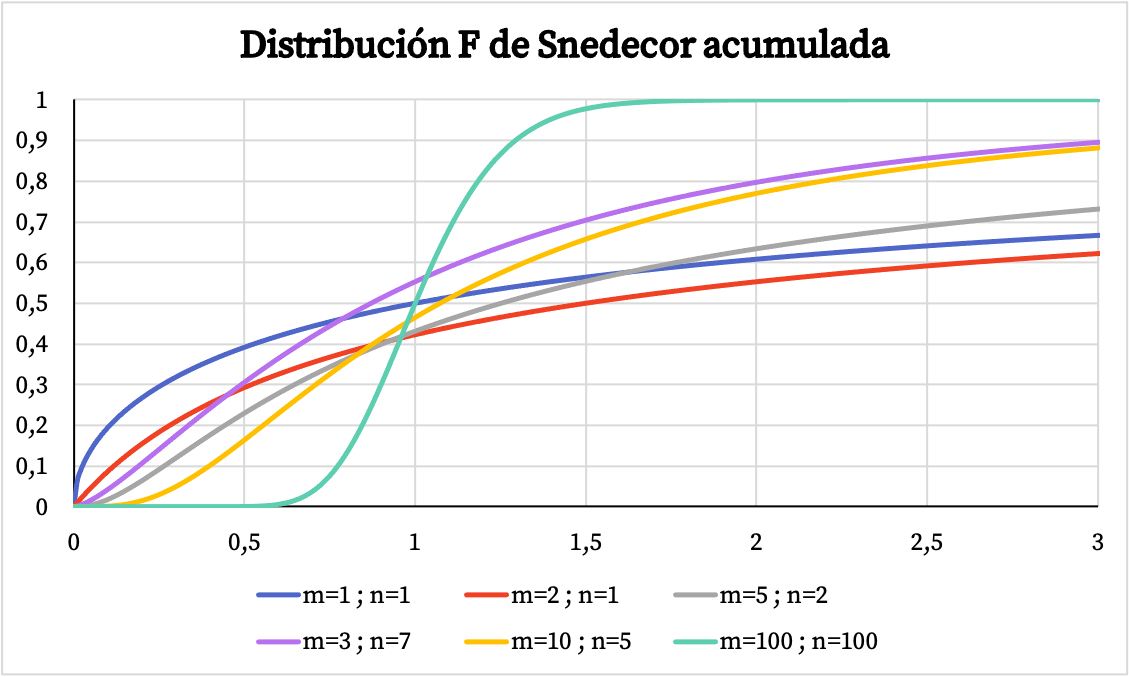
З іншого боку, на графіку нижче ви можете побачити, як змінюється графік кумулятивної функції ймовірності розподілу Snedecor F в залежності від його характерних значень.
Характеристики розподілу Snedecor F
Нарешті, у цьому розділі представлено найважливіші характеристики розподілу Snedecor F.
- Ступені свободи F-розподілу Снедекора, m і n , є двома параметрами, які визначають форму розподілу. Ці характерні значення розподілу Snedecor F є натуральними числами.
![\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Область розподілу Снедекора F складається з усіх дійсних чисел, більших або рівних нулю.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-043df156b055e7088fa83fe733825632_l3.png)
![]()
- Для значень n більше 2 середнє значення розподілу F Снедекора дорівнює n після віднімання n мінус 2.
![\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Коли параметр <em>n</em> більше 2, дисперсію розподілу Снедекора F можна розрахувати за такою формулою:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5861b8fbc6e7aef8cac0eb21cad00c9f_l3.png)
![\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Якщо параметр <em>m</em> більше 2, моду розподілу Снедекора F можна обчислити за таким виразом:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-9a284413da889eec7ac2e9a95e255169_l3.png)
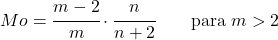
![Rendered by QuickLaTeX.com \displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-06871a7baaf462b75f545a02eac7dd11_l3.png)
- Якщо змінна відповідає F-розподілу Снедекора зі ступенями свободи m і n , то обернена змінна відповідає F-розподілу Снедекора з тими самими ступенями свободи, але змінює порядок своїх значень.
![]()
- Розподіл Стьюдента має такий зв’язок із розподілом Snedecor F:
![]()