Розподіл частоти

за Редакція 4 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке частотні розподіли та як вони досягаються. Ви також знайдете покрокові приклади розподілу частот і, крім того, зможете потренуватися з розв’язаними вправами.

Що таке частотний розподіл?

У статистиці розподіл частот – це таблиця, в якій різні значення вибірки згруповані в рядки, а в кожному стовпці відображається тип частоти кожного значення. Тому розподіл частот використовується для відображення всіх типів частот у наборі даних.

Більш конкретно, розподіл частот включає абсолютну частоту, кумулятивну абсолютну частоту, відносну частоту та кумулятивну відносну частоту.

Однією з характеристик частотних розподілів є те, що вони дуже корисні для узагальнення статистичної вибірки кількісної змінної та якісної змінної.

Як зробити частотний розподіл

Щоб виконати частотний розподіл, необхідно виконати наступні кроки:

Упорядкуйте дані за різними категоріями та створіть таблицю, у якій кожен рядок відповідає категорії.
Обчисліть абсолютну частоту кожної категорії у другому стовпчику таблиці.
Обчисліть кумулятивну абсолютну частоту кожної категорії в третьому стовпчику таблиці.
Обчисліть відносну частоту кожної категорії в четвертому стовпчику таблиці.
Обчисліть кумулятивну відносну частоту кожної категорії в п’ятому стовпці таблиці.
За бажанням можна додати два стовпці, у яких відносна частота та кумулятивна відносна частота обчислюються у відсотках, для цього потрібно просто помножити обидва стовпці на 100.

Приклад розподілу частот

Після того, як ми ознайомилися з визначенням частотного розподілу та теорією його побудови, у цьому розділі крок за кроком розв’язується приклад.

Оцінки, отримані з предмету статистика у класі, який налічує 30 учнів, такі. Побудуйте частотний розподіл набору даних.

$5\ 4\ 7\ 9\ 10\ 6\ 7\ 4\ 8\ 3$

$6\ 9\ 8\ 5\ 6\ 4\ 6\ 2\ 4\ 7$

$8\ 9\ 10\ 5\ 4\ 3\ 6\ 8\ 7\ 5$

Оскільки всі числа можуть бути лише цілими, це дискретна змінна. Тому немає необхідності групувати дані в інтервали.

Отже, щоб зробити розподіл частот, нам потрібно побудувати таблицю, у якій кожне значення буде рядком, а потім нам потрібно знайти абсолютну частоту кожного значення:

➤ Дивіться: як знайти абсолютну частоту

Зверніть увагу, що сума всіх абсолютних частот дорівнює загальній кількості даних. Якщо це правило не дотримується, це означає, що ви забули надати певну інформацію.

Тепер, коли ми знаємо абсолютну частоту, нам потрібно обчислити сукупну абсолютну частоту. Для цього розрахунку у нас є два варіанти: або ми додаємо абсолютну частоту значення плюс усі абсолютні частоти найменших значень, або, навпаки, ми додаємо абсолютну частоту значення плюс кумулятивну абсолютну частоту попереднього значення.

Кумулятивна абсолютна частота останнього значення завжди відповідає загальній кількості даних, ви можете скористатися цим трюком, щоб перевірити правильність обчислень.

Далі нам потрібно визначити відносну частоту, яка обчислюється діленням абсолютної частоти на загальну кількість точок даних (30):

➤ Дивіться: як обчислюється відносна частота

Майте на увазі, що сума всіх відносних частот завжди дорівнює 1, інакше це означає, що певний розрахунок розподілу частот є неправильним.

Нарешті, нам просто потрібно витягти кумулятивну відносну частоту. Щоб зробити це, ви повинні додати відносну частоту відповідного значення плюс усі попередні відносні частоти або, що дорівнює тому ж самому, попередню накопичену відносну частоту:

Коротше кажучи, розподіл частот для всіх частот проблемних даних виглядає наступним чином:

Частотний розподіл для згрупованих даних

Щоб зробити частотний розподіл для даних, згрупованих в інтервали , єдина відмінність полягає в тому, що набір даних спочатку потрібно згрупувати в різні інтервали, але решта обчислень виконується так само, як у частотному розподілі без групування даних.

Як приклад, нижче вирішується задача побудови частотного розподілу для згрупованих даних.

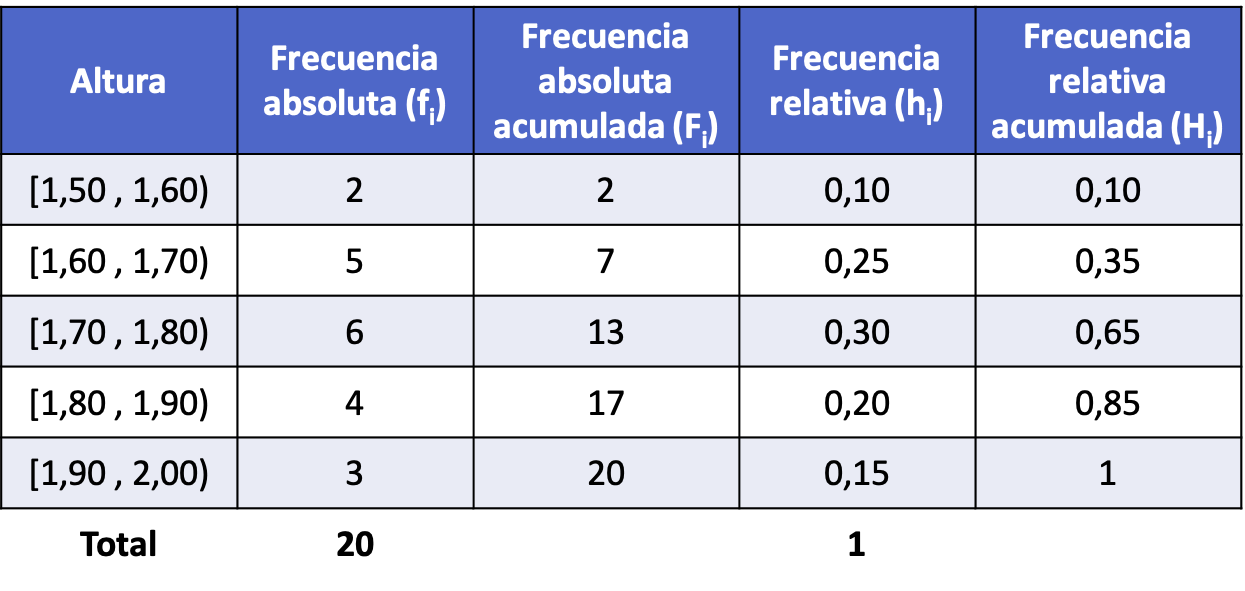
Було виміряно зріст 20 людей і отримано результати, зазначені нижче. Створіть частотний розподіл, розділивши дані на інтервали.

$1,84\ 1,71\ 1,75\ 1,92\ 1,57\ 1,67\ 1,94\ 1,83\ 1,79\ 1,68$

$1,54\ 1,61\ 1,78\ 1,62\ 1,89\ 1,80\ 1,99\ 1,77\ 1,70\ 1,63$

Дані в цій вибірці мають неперервний розподіл, оскільки числа можуть бути десятковими і, отже, приймати будь-які значення. Тому ми зробимо частотний розподіл, групуючи дані в інтервали.

Хоча існує кілька математичних правил створення інтервалів вибірки, у цьому випадку ми просто створимо інтервали шириною 10 десятих.

Отже, після обчислення всіх типів частоти для кожного інтервалу (процедура така ж, як у прикладі вище), розподіл частот із даними, згрупованими в інтервали, виглядає наступним чином:

частотний розподіл для згрупованих даних

Вирішені вправи на розподіл частот

Вправа 1

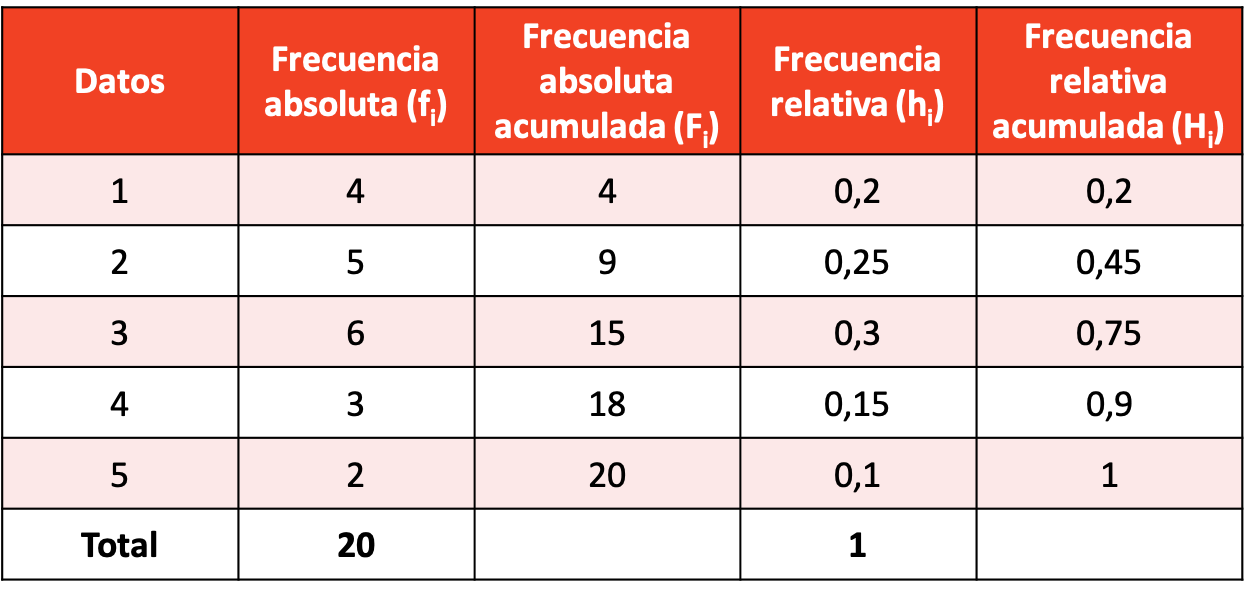
Ми запитали 20 людей, скільки разів вони ходять у кінотеатр на місяць, і ось результати:

$1\ 3\ 4\ 5\ 2\ 3\ 4\ 1\ 2\ 2$

$3\ 1\ 5\ 4\ 3\ 2\ 2\ 3\ 1\ 3$

Зробіть частотний розподіл з отриманою вибіркою даних.

Подивіться рішення

Розподіл частот з розрахунками всіх типів частот такий:

Вправа 2

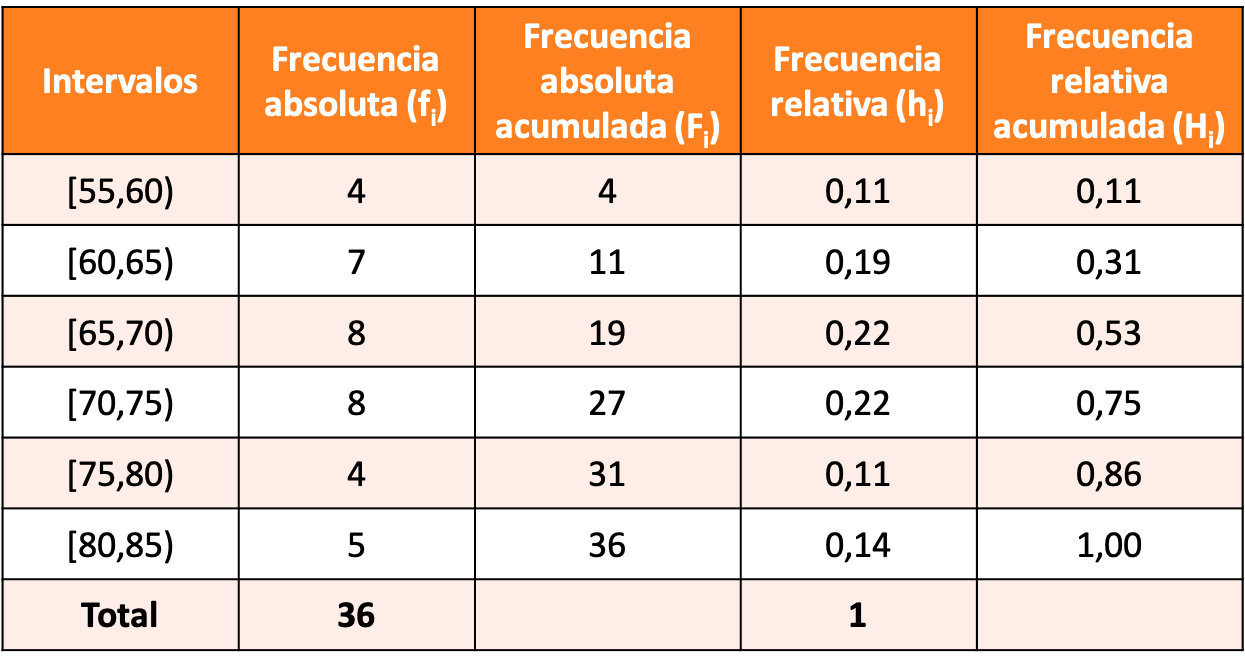
Ви хотіли б провести статистичне дослідження ваги працівників у компанії з 36 працівниками. Ось вага робітників у кілограмах:

$70,8\quad 82,3\quad 65,1\quad 59,4\quad 56,7\quad 63,1$

$83,9\quad 70,0\quad 79,4\quad 80,0\quad 65,4\quad 61,8$

$65,9\quad 74,7\quad 58,1\quad 63,5\quad 69,9\quad 67,2$

$72,1\quad 64,5\quad 81,8\quad 76,4\quad 71,5\quad 67,5$

$61,8\quad 71,3\quad 82,4\quad 62,8\quad 66,5\quad 71,8$

$77,9\quad 75,0\quad 65,6\quad 72,9\quad 63,0\quad 58,1$

Побудуйте частотний розподіл із згрупованими даними, зробивши інтервали по 5 одиниць і нехай перший інтервал буде [55,60].

Подивіться рішення

Розв’язком вправи є такий розподіл частот:

Розв’язана вправа на частотну таблицю для даних, згрупованих в інтервали

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше