Як інтерпретувати графік масштабу та розташування: із прикладами

Масштабована діаграма розташування — це тип діаграми, який відображає підібрані значення регресійної моделі вздовж осі х і квадратний корінь із стандартизованих залишків уздовж осі у.

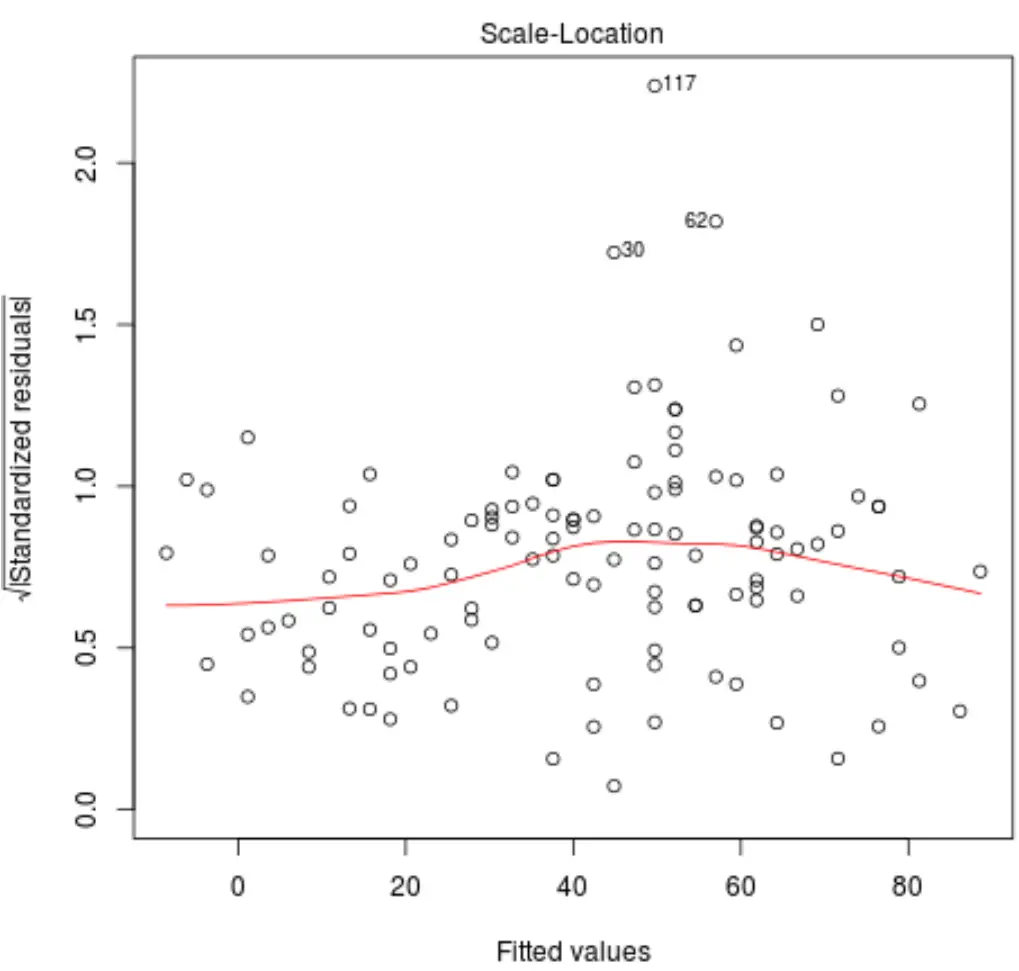
Дивлячись на цей графік, ми перевіряємо дві речі:

1. Переконайтеся, що червона лінія розташована приблизно горизонтально на графіку. Якщо це так, то припущення про гомоскедастичність , ймовірно, задовольняється для даної моделі регресії. Тобто розподіл залишків приблизно однаковий для всіх підігнаних значень.

2. Перевірте, чи немає чіткої тенденції серед залишків. Іншими словами, залишки повинні бути випадковим чином розкидані навколо червоної лінії з приблизно однаковою мінливістю для всіх підігнаних значень.

Побудова графіка масштабу та розташування в R

Ми можемо використати наступний код, щоб підібрати просту модель лінійної регресії в R і побудувати графік масштабу та розташування для отриманої моделі:

 #fit simple linear regression model
model <- lm(Ozone ~ Temp, data = airquality)

#produce scale-location plot
plot(model)

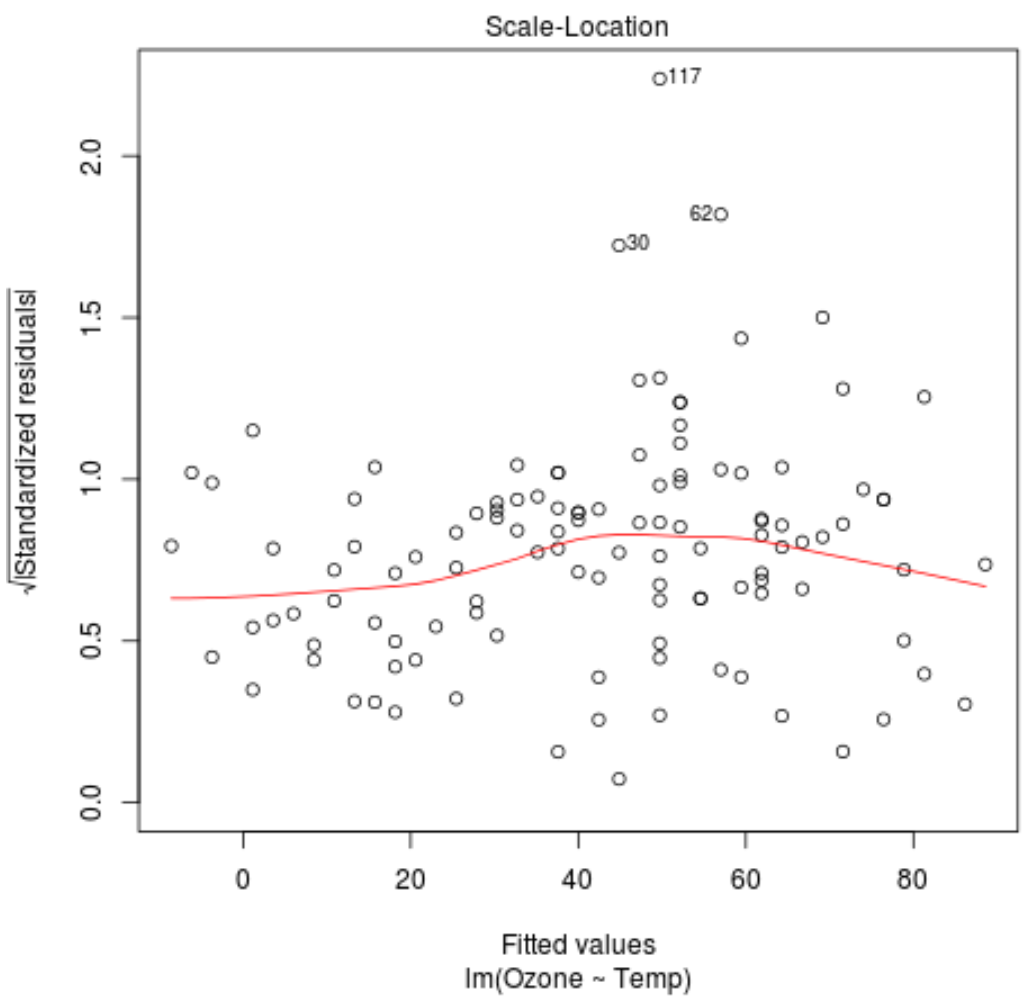
Ми можемо спостерігати наступні дві речі на графіку масштабу-розташування цієї регресійної моделі.

1. Червона лінія проходить приблизно горизонтально на ділянці. Якщо це так, то припущення про гомоскедастичність задовольняється для даної моделі регресії. Тобто розподіл залишків приблизно однаковий для всіх підігнаних значень.

2. Перевірте, чи немає чіткої тенденції серед залишків. Іншими словами, залишки повинні бути випадковим чином розкидані навколо червоної лінії з приблизно однаковою мінливістю для всіх підігнаних значень.

Технічні примітки

Три спостереження з набору даних із найвищими стандартизованими залишками позначені на графіку.

Ми бачимо, що спостереження в рядках 30, 62 і 117 мають найвищі стандартизовані залишки.

Це не обов’язково означає, що ці спостереження викидаються, але ви можете переглянути вихідні дані, щоб уважніше вивчити ці спостереження.

Хоча ми бачимо, що червона лінія розташована приблизно горизонтально на графіку розташування масштабу, це лише візуальний спосіб побачити, чи виконується припущення про гомоскедастичність.

Формальним статистичним тестом, який ми можемо використовувати, щоб побачити, чи виконується припущення про гомоскедастичність, є тест Брейша-Пейгана .

Тест Брейша-Пагана в Р

У наступному коді показано, як використовувати функцію bptest() пакета lmtest для виконання тесту Брейша-Пагана в R:

 #load lmtest package
library(lmtest)

#perform Breusch-Pagan Test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 1.4798, df = 1, p-value = 0.2238

Тест Брейша-Пейгана використовує такі нульові та альтернативні гіпотези:

• Нульова гіпотеза (H ₀ ): залишки гомоскедастичні (тобто рівномірно розподілені)
• Альтернативна гіпотеза ( _HA ): залишки гетероскедастичні (тобто нерівномірно розподілені)

З результату ми бачимо, що p-значення тесту становить 0,2238 . Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу. У нас немає достатніх доказів, щоб стверджувати, що гетероскедастичність присутня в регресійній моделі.

Цей результат відповідає нашому візуальному огляду червоної лінії на графіку розташування масштабу.

Додаткові ресурси

Розуміння гетероскедастичності в регресійному аналізі
Як створити ділянку залишків у R
Як виконати тест Брейша-Пейгана в R