Вступ до рівномірного розподілу

Рівномірний розподіл — це розподіл ймовірностей, у якому кожне значення між інтервалом від a до b має однакову ймовірність появи.

Якщо випадкова величина X має рівномірний розподіл, то ймовірність того, що X приймає значення від x ₁ до x ₂ , можна знайти за такою формулою:

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – a)

золото:

• x ₁ : нижча процентна вартість
• x ₂ : верхнє значення інтересу
• a: мінімально можливе значення
• b: максимально можливе значення

Наприклад, припустимо, що вага дельфінів рівномірно розподілена між 100 і 150 фунтами.

Якщо ми вибираємо дельфіна навмання, ми можемо використати наведену вище формулу, щоб визначити ймовірність того, що вибраний дельфін важить від 120 до 130 фунтів:

• P(120 < X < 130) = (130 – 120) / (150 – 100)
• P(120 < X < 130) = 10/50
• P(120 < X < 130) = 0,2

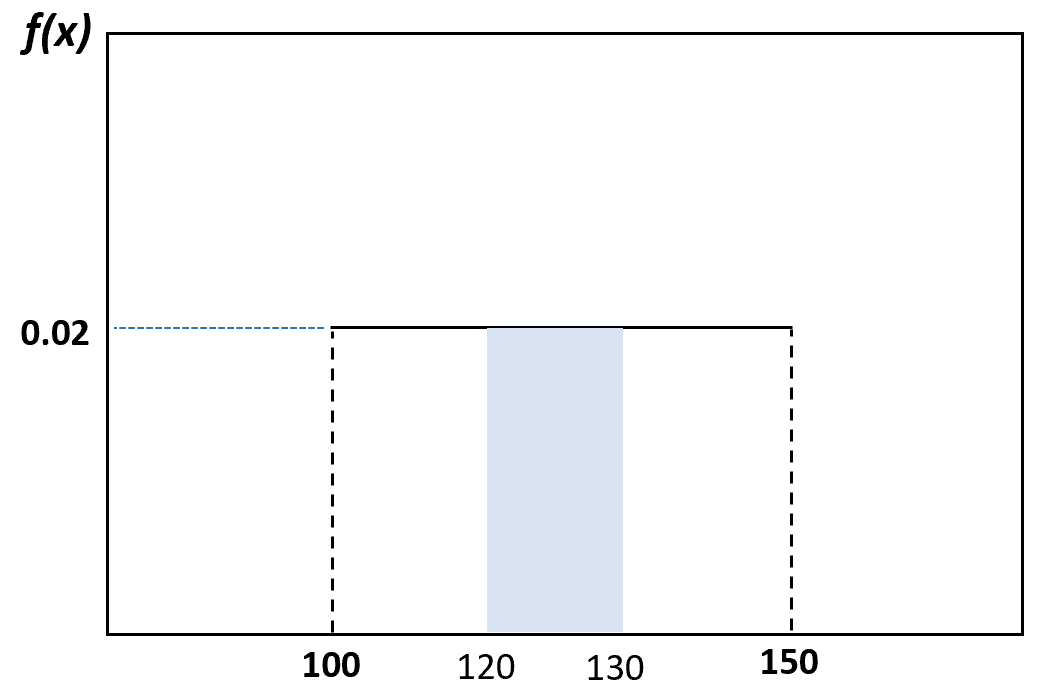
Імовірність того, що обраний дельфін важить від 120 до 130 фунтів, дорівнює 0,2 .

Візуалізуйте рівномірний розподіл

Якщо ми створимо графік щільності для візуалізації рівномірного розподілу, він виглядатиме так:

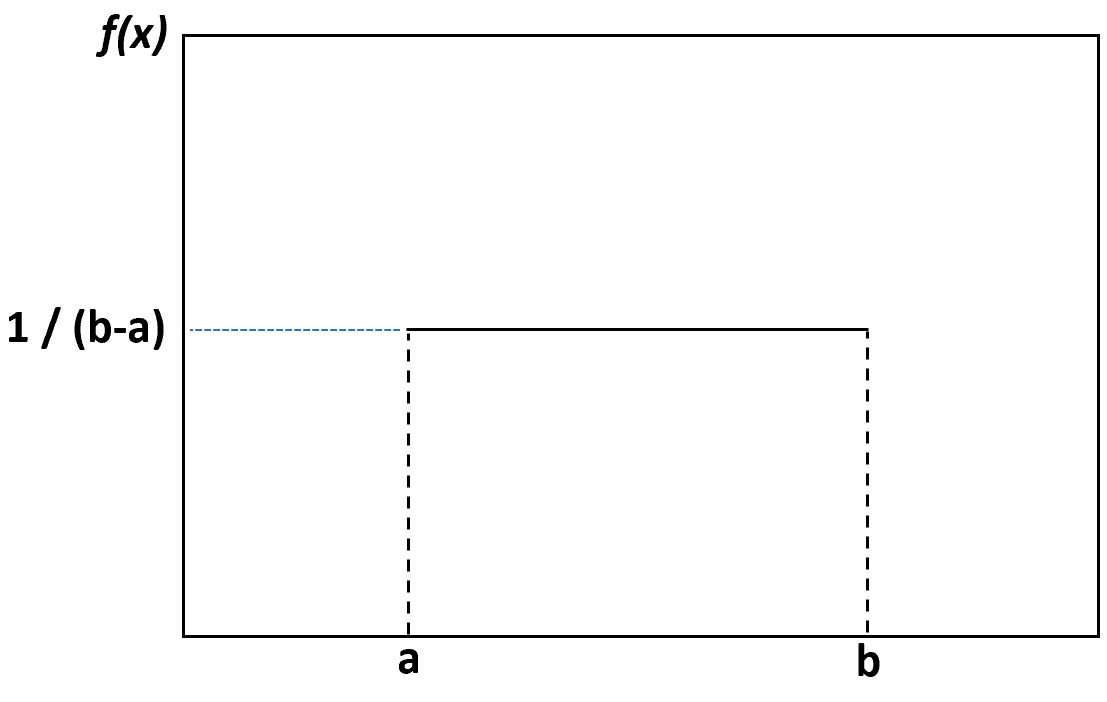
Кожне значення між нижньою межею a та верхньою межею b має однакову ймовірність виникнення, а будь-яке значення поза цими межами має нульову ймовірність.

Наприклад, у попередньому прикладі ми сказали, що вага дельфінів рівномірно розподілена між 100 і 150 фунтами. Ось як візуалізувати цей розподіл:

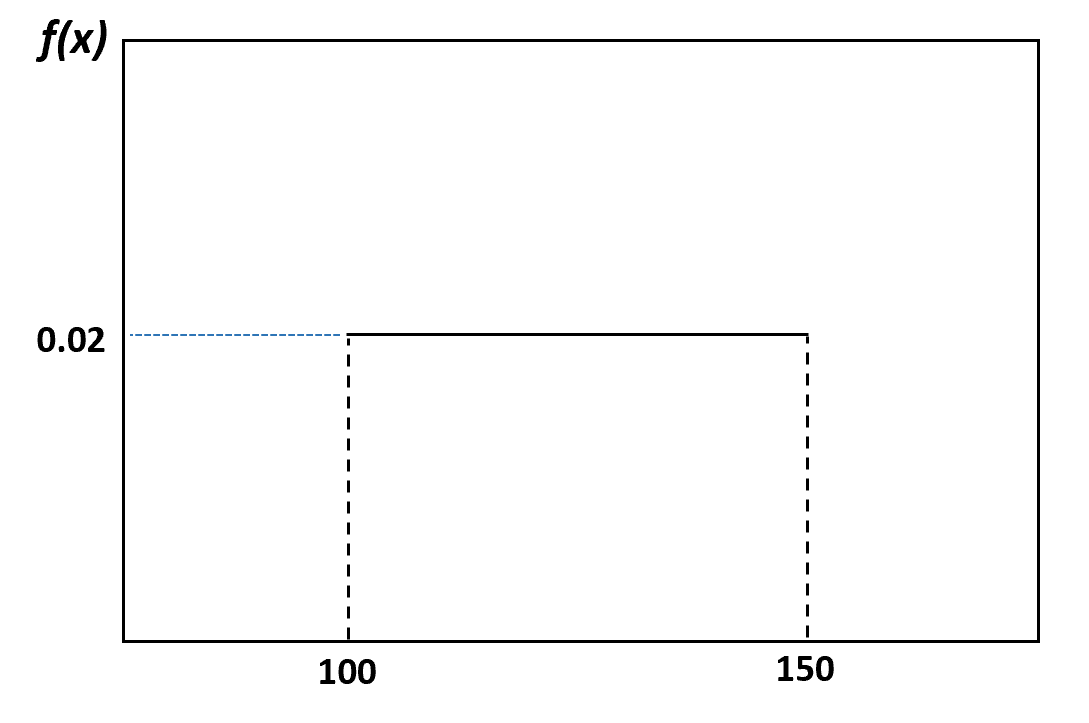
А ймовірність того, що навмання обраний дельфін важить від 120 до 130 фунтів, можна візуалізувати таким чином:

Властивості рівномірного розподілу

Рівномірний розподіл має такі властивості:

• Середнє: (a + b) / 2
• Медіана: (a + b) / 2
• Стандартне відхилення: √ (b – a) ² / 12
• Різниця: (б – а) ² / 12

Наприклад, припустимо, що вага дельфінів рівномірно розподілена між 100 і 150 фунтами.

Ми могли б обчислити такі властивості для цього розподілу:

• Середня вага: (a + b) / 2 = (150 + 100) / 2 = 125
• Середня вага: (a + b) / 2 = (150 + 100) / 2 = 125
• Стандартне відхилення ваги: √ (150 – 100) ² / 12 = 14,43
• Варіація ваги: (150 – 100) ² / 12 = 208,33

Проблеми з єдиною практикою розподілу

Використовуйте наведені нижче практичні завдання, щоб перевірити свої знання про рівномірний розподіл.

Питання 1: Автобус приїжджає на зупинку кожні 20 хвилин. Якщо ви приїдете на зупинку, яка ймовірність того, що автобус прибуде через 8 хвилин або менше?

Рішення 1: мінімальний час очікування становить 0 хвилин, а максимальний – 20 хвилин. Нижнє відсоткове значення становить 0 хвилин, а верхнє відсоткове значення – 8 хвилин.

Отже, ми розрахуємо ймовірність наступним чином:

P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0,4 .

Запитання 2: Тривалість гри НБА рівномірно розподіляється між 120 і 170 хвилинами. Яка ймовірність того, що навмання вибрана гра NBA триватиме більше 155 хвилин?

Рішення 2: мінімальна тривалість – 120 хвилин, а максимальна – 170 хвилин. Нижнє відсоткове значення становить 155 хвилин, а верхнє відсоткове значення – 170 хвилин.

Отже, ми розрахуємо ймовірність наступним чином:

P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0,3 .

Запитання 3: Вага певного виду жаби рівномірно розподілена між 15 і 25 грамами. Якщо ви навмання виберете жабу, яка ймовірність того, що вона важить від 17 до 19 грамів?

Рішення 3: мінімальна вага становить 15 грамів, а максимальна вага — 25 грамів. Нижнє відсоткове значення становить 17 грамів, а верхнє відсоткове значення – 19 грамів.

Отже, ми розрахуємо ймовірність наступним чином:

P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0,2 .

Примітка: ми можемо використовувати калькулятор рівномірного розподілу, щоб перевірити наші відповіді на кожну з цих задач.