Секторні діаграми

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке кругові діаграми, як побудувати кругову діаграму, і, крім того, ви зможете побачити покрокову вправу цього типу статистичного графіка.

Що таке кругова діаграма?

Кругова діаграма або кругова діаграма — це тип статистичної діаграми, у якій дані представлені колом, поділеним на сектори, таким чином, що кут кожного сектора пропорційний його відповідній частоті.

Іншими словами, чим вища частота значення, тим більший відповідний йому сектор на діаграмі.

Тому секторні діаграми використовуються для візуального аналізу частоти кожного значення. У статистиці ці типи графіків в основному використовуються для представлення якісних змінних.

Як зробити кругову діаграму

Щоб створити секторну діаграму, виконайте наведені нижче дії.

Зберіть статистичні дані з вибірки, яку ви хочете проаналізувати, і створіть частотну таблицю.
Обчисліть кут кожного сектора діаграми . Для цього необхідно скористатися такою формулою:

$\alpha_i= f_i \cdot \cfrac{360^o}{N}$

золото

$\alpha_i$

– кут сектора i ,

$f_i$

його абсолютна частота і

$N$

загальна кількість даних.

За обчисленими кутами зобразіть сектори на круговому графіку за допомогою кутоміра.
Обчисліть відсоток кожного сектора на діаграмі за такою формулою:

$\%_i= f_i \cdot \cfrac{100}{N}$

золото

$\%_i$

є відсотком сектора i ,

$f_i$

його абсолютна частота і

$N$

загальна кількість даних.

Вкажіть на схемі відсоток кожного сектора.

Приклад кругової діаграми

Щоб ви могли точно побачити, як створити секторну діаграму, нижче наведено покроковий приклад:

50 людей запитали про їх улюблене місто, і дані були зібрані в наступній таблиці. Представте ці статистичні дані у вигляді кругової діаграми.

Перш за все, ми повинні обчислити кут, який відповідає кожному сектору, тому ми використовуємо таку формулу для кожного значення:

$\alpha_i = f_i \cdot \cfrac{360^o}{N}$

золото

$\alpha_i$

кут кожного сектора,

$f_i$

його частота і

$N$

загальна кількість спостережень.

Наприклад, розрахунок кута сектора, який відповідає першому значенню:

$\alpha_{Londres}=16 \cdot \cfrac{360^o}{50} = 115,2^o$

А потім малюємо в колі сектор, відповідний куту, обчисленому за допомогою кутоміру:

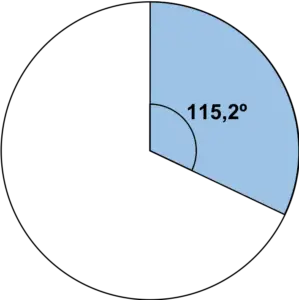
Повторюємо ту саму процедуру для всіх значень:

$\alpha_{Paris}=12 \cdot \cfrac{360^o}{50}=86,4^o$

$\alpha_{Nueva \ York}=9\cdot \cfrac{360^o}{50}=64,8^o$

$\alpha_{Roma}= 7 \cdot \cfrac{360^o}{50} = 50,4^o$

$\alpha_{Otras}=6 \cdot \cfrac{360^o}{50} = 43,2^o$

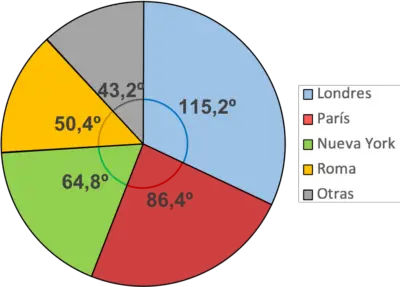
Рекомендується пофарбувати кожен сектор іншим кольором, щоб їх було легше розрізняти. Так само слід додати легенду, щоб вказати значення кожного кольору.

Коли всі сектори представлені, необхідно обчислити відсоток, який відповідає кожному. Для цього застосовуємо таку формулу:

$\%_i = f_i \cdot \cfrac{100}{N}$

золото

$\%_i$

це відсоток кожного сектора,

$f_i$

його частота і

$N$

загальна кількість даних у статистичному дослідженні.

Отже, відсоток кожного сектора становить:

$\%_{Londres} \cdot \cfrac{100}{N}=16\cdot \cfrac{100}{50}=32\%$

$\%_{Paris}=12 \cdot \cfrac{100}{50}=24\%$

$\%_{Nueva \ York}}=9\cdot\cfrac{100}{50}=18\%$

$\%_{Roma}}=7\cdot\cfrac{100}{50}=14\%$

$\%_{Otras}=6\cdot\cfrac{100}{50}=12\%$

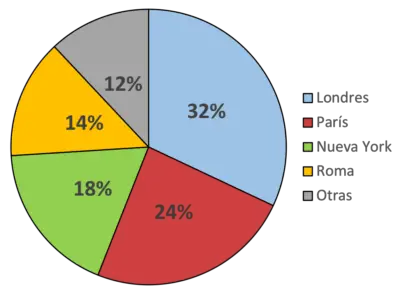
За допомогою цієї діаграми ми вказуємо, що, наприклад, блакитний колір представляє місто Лондон, яке подобається більшості людей (32% людей). Так само зелений колір представляє Нью-Йорк, який є улюбленим містом 18% респондентів.

Переваги та недоліки секторної діаграми

Завдяки своїм характеристикам кругові діаграми мають такі переваги та недоліки:

Перевага:

Це дуже наочний статистичний графік, який дозволяє швидко аналізувати та робити висновки.
Це дуже корисно для графіків якісних даних.
Якщо це зробити за допомогою комп’ютера, наприклад, за допомогою Excel, це зробити дуже швидко.

Недоліки:

Коли на діаграмі багато різних секторів, читання діаграми може стати складнішим. У цьому випадку рекомендується згрупувати маленькі сектори в один сектор під назвою «Інші».
Існують інші типи статистичних діаграм, які більше підходять для представлення кількісних змінних або часових рядів.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке кругова діаграма?

Як зробити кругову діаграму

Приклад кругової діаграми

Переваги та недоліки секторної діаграми

Про автора

Редакція

Додати коментар