Як обчислити середню квадратичну помилку (rmse) в excel

У статистиці регресійний аналіз — це техніка, яку ми використовуємо для розуміння зв’язку між змінною предиктора x і змінною відповіді y.

Коли ми виконуємо регресійний аналіз, ми отримуємо модель, яка повідомляє нам прогнозоване значення змінної відповіді на основі значення змінної предиктора.

Один із способів оцінити, наскільки добре наша модель відповідає даному набору даних, — обчислити середню квадратичну помилку , яка є показником, який повідомляє нам, наскільки наші прогнозовані значення в середньому далекі від спостережуваних значень.

Формула для визначення середньої квадратичної помилки, більш відомої як RMSE , є:

RMSE = √[ Σ(P _i – O _i ) ² / n ]

золото:

• Σ – химерний символ, який означає «сума»
• P _i – прогнозоване значення для ^i-го спостереження в наборі даних
• O _i — спостережене значення для ^i-го спостереження в наборі даних
• n – розмір вибірки

Технічні примітки :

• Середню квадратичну похибку можна обчислити для будь-якого типу моделі, яка виробляє прогнозовані значення, які потім можна порівняти зі спостережуваними значеннями набору даних.
• Середньоквадратичну похибку також іноді називають середнім квадратичним відхиленням, яке часто називають RMSD.

Далі розглянемо приклад того, як обчислити середню квадратичну помилку в Excel.

Як обчислити середню квадратичну помилку в Excel

В Excel немає вбудованої функції для обчислення RMSE, але ми можемо досить легко обчислити це за допомогою однієї формули. Ми покажемо, як розрахувати RMSE для двох різних сценаріїв.

Сценарій 1

У сценарії ви можете мати один стовпець, що містить прогнозовані значення з вашої моделі, і інший стовпець, що містить спостережувані значення. На зображенні нижче показано приклад цього сценарію:

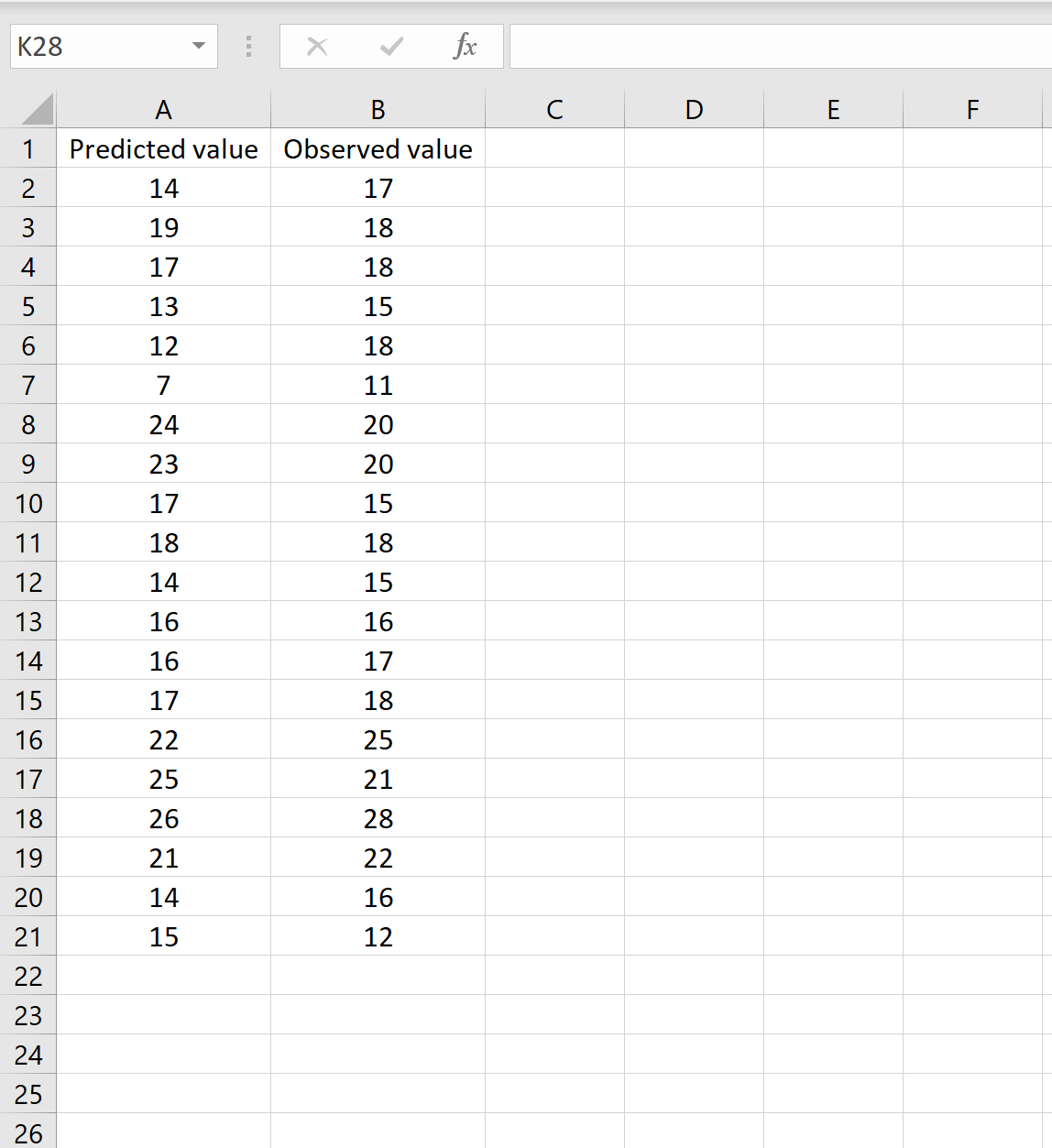
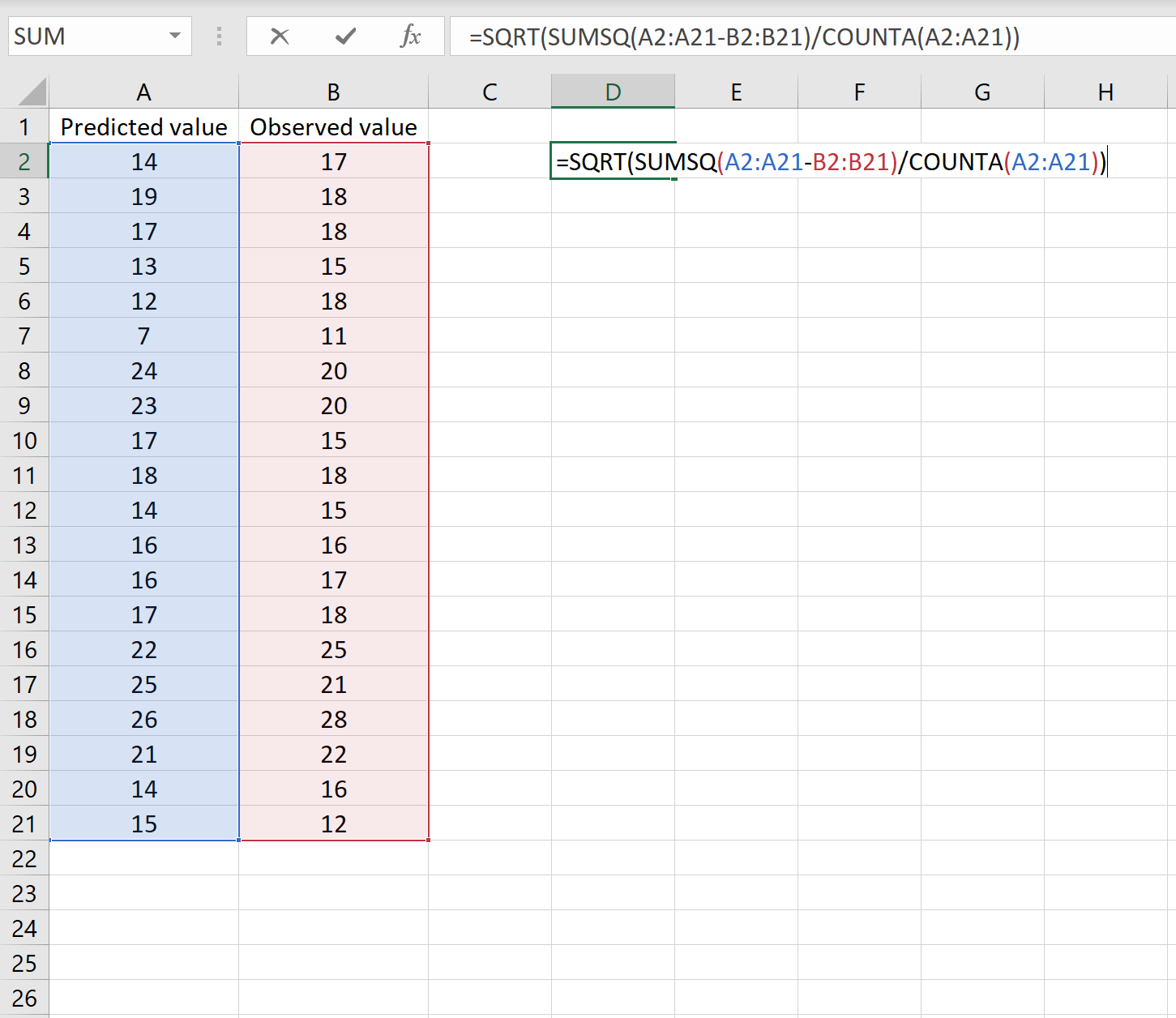
Якщо так, ви можете обчислити RMSE, ввівши таку формулу в будь-яку комірку та натиснувши CTRL+SHIFT+ENTER:

=SQRT(SUMSQ(A2:A21-B2:B21) / КІЛЬКІСТЬ(A2:A21))

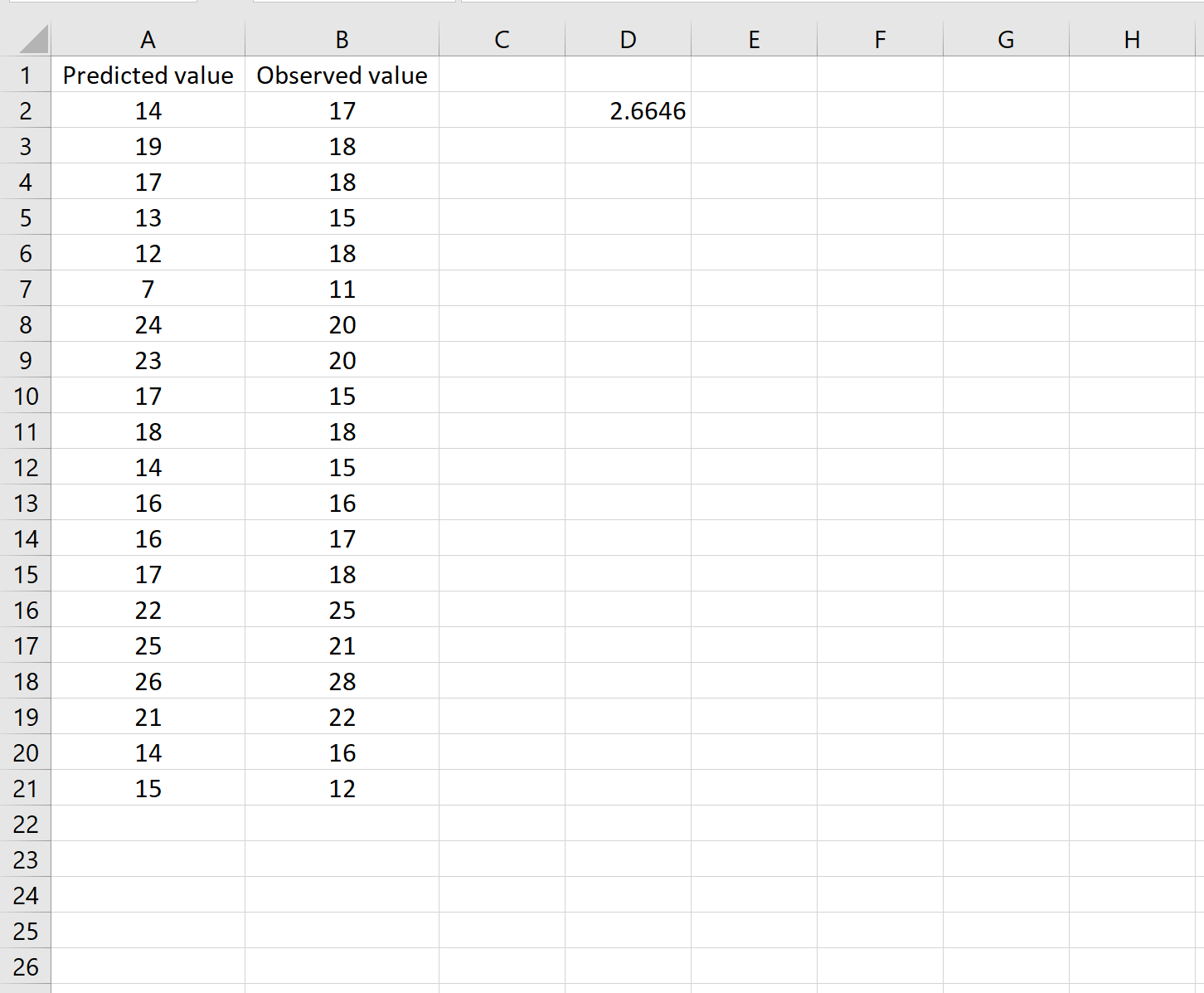
Це говорить нам, що середня квадратична помилка становить 2,6646 .

Формула може здатися трохи складною, але вона має сенс, коли ви її розберете:

= SQRT( SUMSQ(A2:A21-B2:B21) / КІЛЬКІСТЬ(A2:A21) )

• Спочатку ми обчислюємо суму квадратів різниць між прогнозованими та спостережуваними значеннями за допомогою функції SUMSQ() .
• Далі ми ділимо на розмір вибірки набору даних за допомогою функції COUNTA() , яка підраховує кількість клітинок у діапазоні, які не є порожніми.
• Нарешті, ми беремо квадратний корінь із усього обчислення за допомогою функції SQRT() .

Сценарій 2

В іншому випадку ви, можливо, вже обчислили різницю між прогнозованими та спостережуваними значеннями. У цьому випадку у вас буде лише одна колонка, яка показуватиме відмінності.

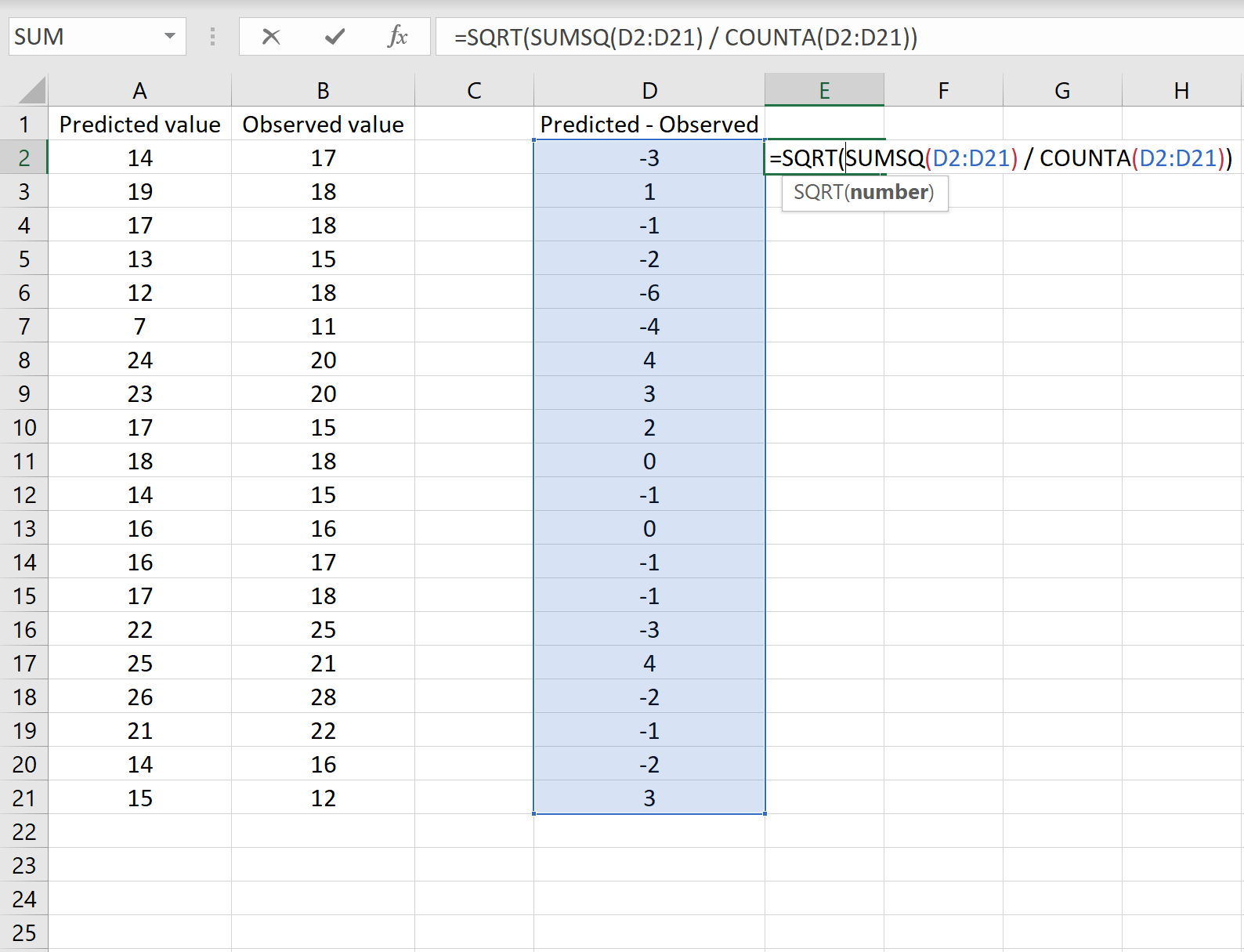
На зображенні нижче показано приклад цього сценарію. Прогнозовані значення показані в стовпці A, спостережувані значення в стовпці B, а різниця між прогнозованими і спостережуваними значеннями в стовпці D:

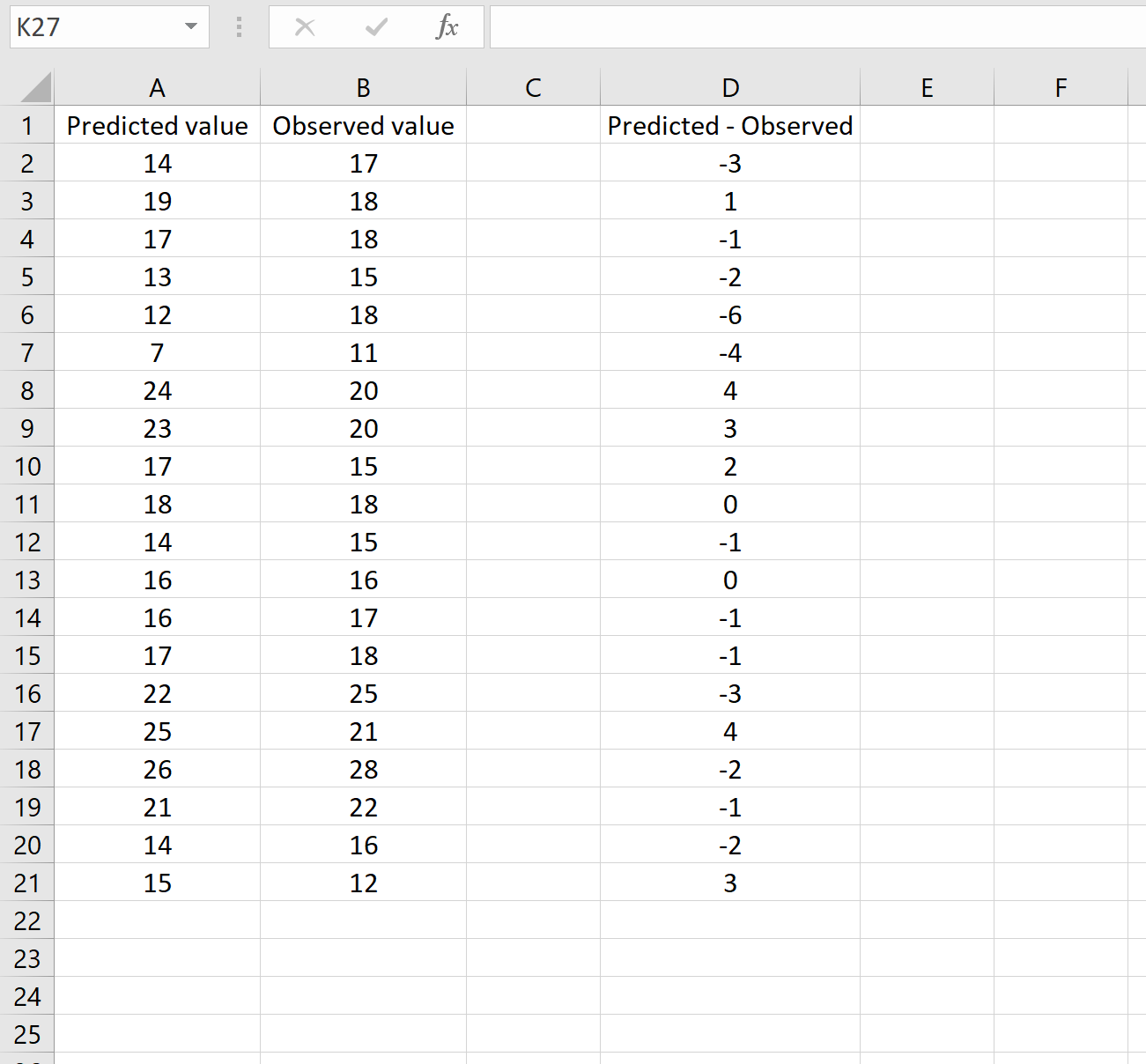
Якщо так, ви можете обчислити RMSE, ввівши таку формулу в будь-яку комірку та натиснувши CTRL+SHIFT+ENTER:

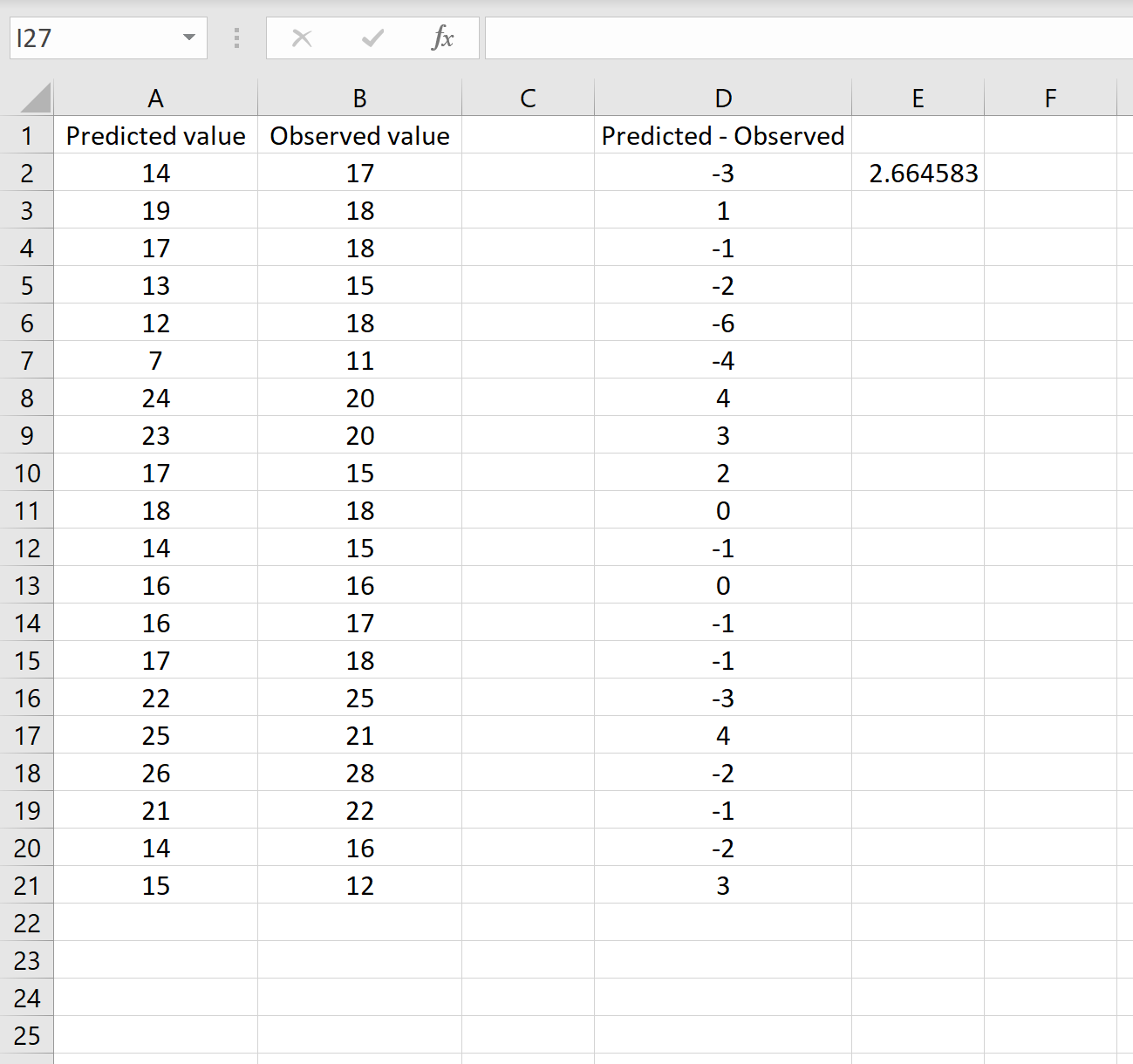
=SQRT(SUMSQ(D2:D21) / КІЛЬКІСТЬ(D2:D21))

Це говорить нам, що середня квадратична помилка становить 2,6646 , що відповідає результату, отриманому в першому сценарії. Це підтверджує, що ці два підходи до розрахунку RMSE еквівалентні.

Формула, яку ми використовували в цьому сценарії, лише трохи відрізняється від тієї, яку ми використовували в попередньому сценарії:

= SQRT( SUMSQ(D2:D21) / COUNT(D2:D21) )

• Оскільки ми вже розрахували різницю між прогнозованими та спостережуваними значеннями в стовпці D, ми можемо обчислити суму квадратів різниць за допомогою функції SUMSQ().   функція тільки зі значеннями зі стовпця D.
• Далі ми ділимо на розмір вибірки набору даних за допомогою функції COUNTA() , яка підраховує кількість клітинок у діапазоні, які не є порожніми.
• Нарешті, ми беремо квадратний корінь із усього обчислення за допомогою функції SQRT() .

Як інтерпретувати RMSE

Як згадувалося раніше, RMSE є корисним способом побачити, наскільки добре регресійна модель (або будь-яка модель, що виробляє прогнозовані значення) здатна «відповідати» набору даних.

Чим більше RMSE, тим більша різниця між прогнозованими та спостережуваними значеннями, тобто тим гірше модель регресії відповідає даним. Навпаки, чим менший RMSE, тим краще модель може відповідати даним.

Особливо корисним може бути порівняння RMSE двох різних моделей, щоб побачити, яка модель найкраще відповідає даним.

Щоб отримати додаткові посібники з Excel, обов’язково ознайомтеся з нашою сторінкою посібників Excel , на якій перераховано всі посібники Excel зі статистики.