Симетричний розподіл

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті ви дізнаєтесь, що таке симетричні розподіли, приклади симетричних розподілів і як визначити, чи є розподіл симетричним чи асиметричним.

Що таке симетричний розподіл?

У статистиці симетричним розподілом є такий, який має однакову кількість значень ліворуч від середнього, як і праворуч від середнього. Іншими словами, у симетричному розподілі середнє є віссю симетрії.

Наприклад, нормальний розподіл є симетричним розподілом.

У всіх симетричних розподілах середнє дорівнює медіані. Але якщо розподіл також унімодальний (статистична мода є одним значенням), середнє, медіана та мода еквівалентні.

Логічно, щоб повністю зрозуміти, що таке симетричний розподіл, вам потрібно чітко знати, що таке середнє, медіана та мода. Ви можете переглянути значення цих статистичних концепцій тут:

➤ Дивіться: Що таке середнє, медіана та мода?

Приклади симетричних розподілів

Розглядаючи визначення симетричного розподілу, приклад цього типу розподілу показано нижче:

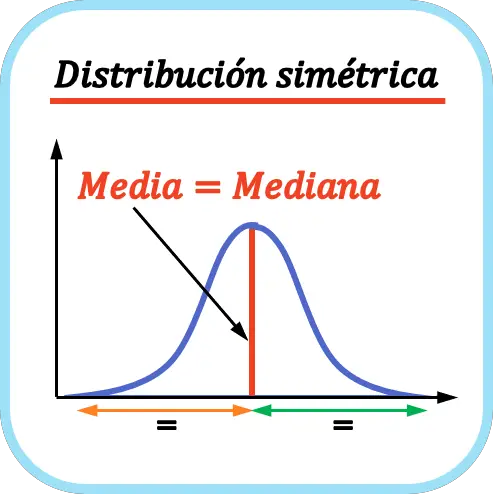
Як показано на графіку, розподіл є симетричним, оскільки середнє значення лежить прямо посередині всіх даних, тобто хвіст ліворуч кривої такий самий, як і хвіст праворуч. У цьому випадку середнє значення, медіана та мода однакові, оскільки мода унімодальна.

Двома яскравими прикладами двох різних типів симетричних розподілів ймовірностей є нормальний розподіл і рівномірний розподіл, оскільки вони мають однакову кількість значень ліворуч і праворуч від середнього.

З іншого боку, розподіл також може бути симетричним і бімодальним, тобто мати два режими. Подивіться на наступний приклад:

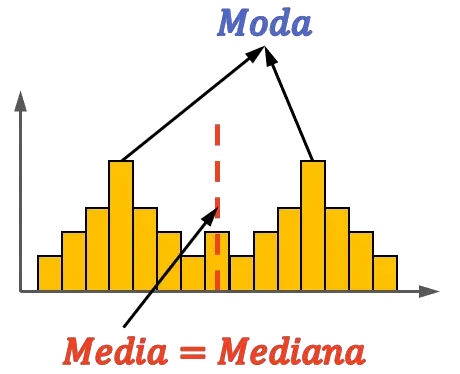
Як ви можете бачити в цьому іншому прикладі, бімодальний розподіл також може бути симетричним, оскільки він може мати середнє та медіану в центрі незалежно від інших значень. Однак у цьому випадку мода не обов’язково повинна дорівнювати середньому і моді.

Інші типи розподілів за їх симетричністю

Крім симетричних розподілів, існує ще два види асиметричних розподілів.

Симетричний розподіл : розподіл має однакову кількість значень ліворуч і праворуч від середнього.
Позитивно викривлений розподіл : розподіл має більше різних значень праворуч від середнього, ніж ліворуч.
Негативно викривлений розподіл : розподіл має більше різних значень ліворуч від середнього, ніж праворуч.

Як визначити, чи є розподіл симетричним

Щоб визначити, чи є розподіл симетричним чи ні, ми повинні обчислити коефіцієнт асиметрії Пірсона, формула якого:

$A_p=\cfrac{\mu-Mo}{\sigma}$

золото

$A_p$

– коефіцієнт Пірсона,

$\mu$

середнє арифметичне,

$Mo$

режим (статистика) і

$\sigma$

стандартне відхилення.

Таким чином, залежно від знака коефіцієнта асиметрії Пірсона розподіл буде симетричним або асиметричним:

Якщо коефіцієнт асиметрії Пірсона додатний, це означає, що розподіл має позитивну асимметрию.
Якщо коефіцієнт асиметрії Пірсона негативний, це означає, що розподіл має негативну асиметрію.
Якщо коефіцієнт асиметрії Пірсона дорівнює нулю, це означає, що розподіл є симетричним.

Однак коефіцієнт Пірсона можна розрахувати лише за унімодального розподілу, інакше необхідно використовувати коефіцієнт асиметрії Фішера, формула якого має наступний вигляд:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\mu\right)^3}{N\cdot \sigma ^3}$

золото

$\mu$

середнє арифметичне,

$\sigma$

стандартне відхилення і

$N$

загальна кількість даних.

Інтерпретація коефіцієнта асиметрії Фішера ідентична коефіцієнту Пірсона: якщо він додатний, це означає, що розподіл є позитивно асиметричним, якщо він від’ємний, то розподіл є негативно асиметричним, а якщо він дорівнює нулю, це означає, що розподіл є симетричним.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше