Як виконати сплайн-регресію в r (з прикладом)

Сплайн-регресія – це тип регресії, який використовується, коли є точки або «вузли», де шаблон у даних різко змінюється, а лінійна регресія та поліноміальна регресія недостатньо гнучкі, щоб узгодити дані.

Наступний покроковий приклад показує, як виконати сплайнову регресію в R.

Крок 1: Створіть дані

Спочатку давайте створимо набір даних у R із двома змінними та створимо діаграму розсіювання, щоб візуалізувати зв’язок між змінними:

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

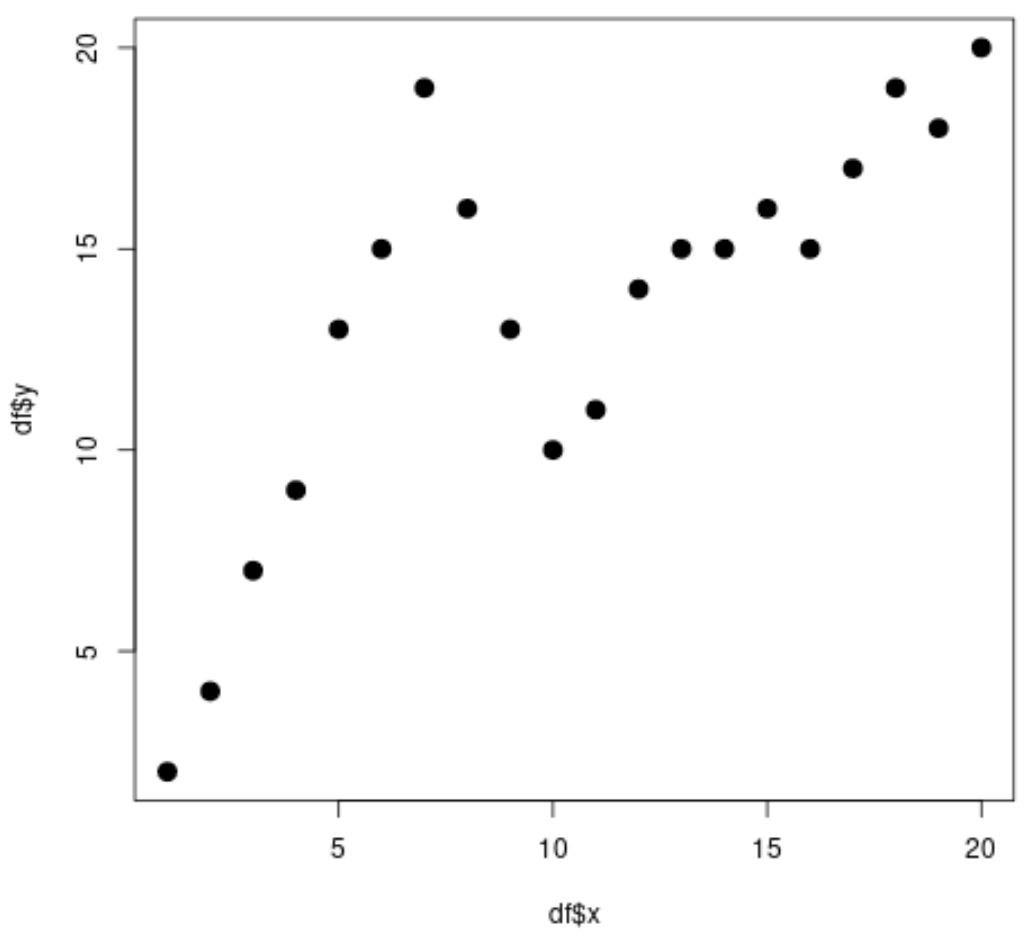
Очевидно, що зв’язок між x і y є нелінійним, і здається, що є дві точки або «вузли», де шаблон у даних раптово змінюється при x=7 і x=10.

Крок 2. Підберіть просту модель лінійної регресії

Давайте скористаємося функцією lm() , щоб підібрати просту модель лінійної регресії до цього набору даних і побудувати лінію регресії на діаграмі розсіювання:

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

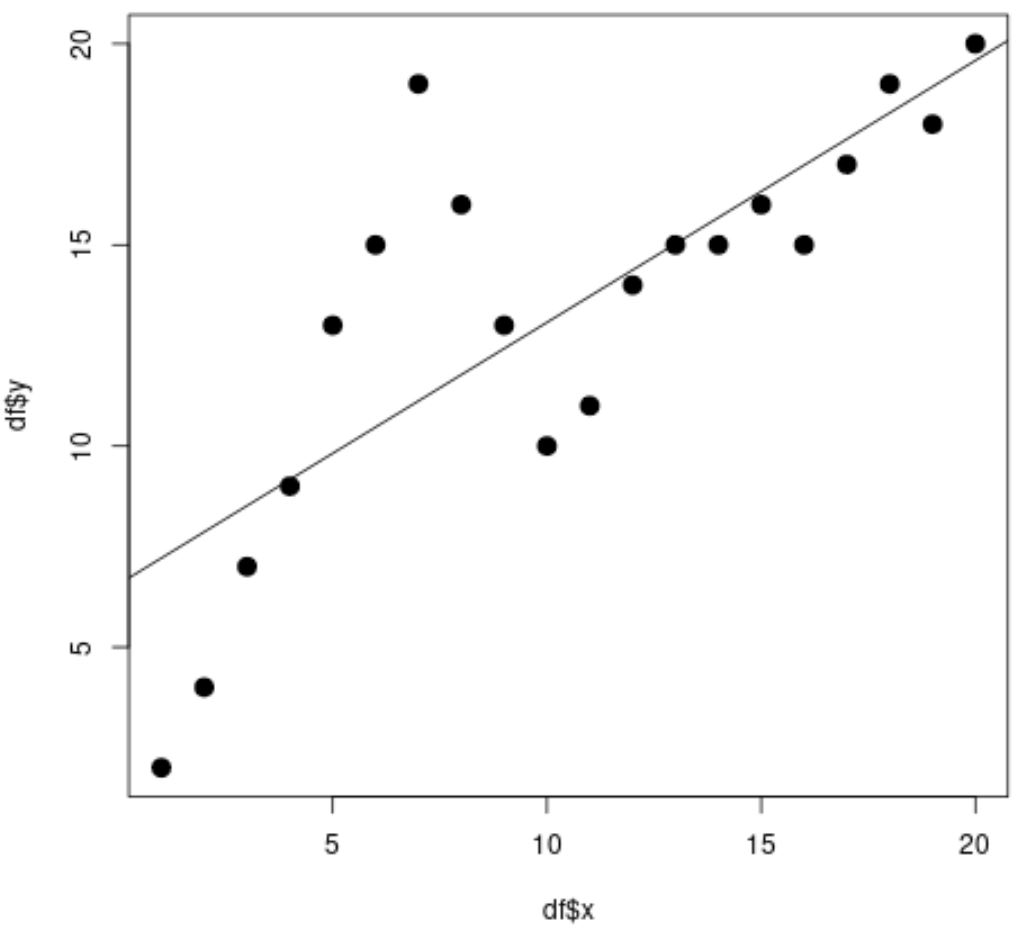
З діаграми розсіювання ми бачимо, що лінія простої лінійної регресії погано відповідає даним.

З результатів моделі ми також бачимо, що скориговане значення R-квадрат становить 0,5903 .

Ми порівняємо це зі скоригованим значенням R-квадрат сплайн-моделі.

Крок 3. Підберіть модель сплайн-регресії

Далі скористаємося функцією bs() із пакета сплайнів , щоб підібрати сплайн-регресійну модель із двома вузлами, а потім побудуємо підібрану модель на діаграмі розсіювання:

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

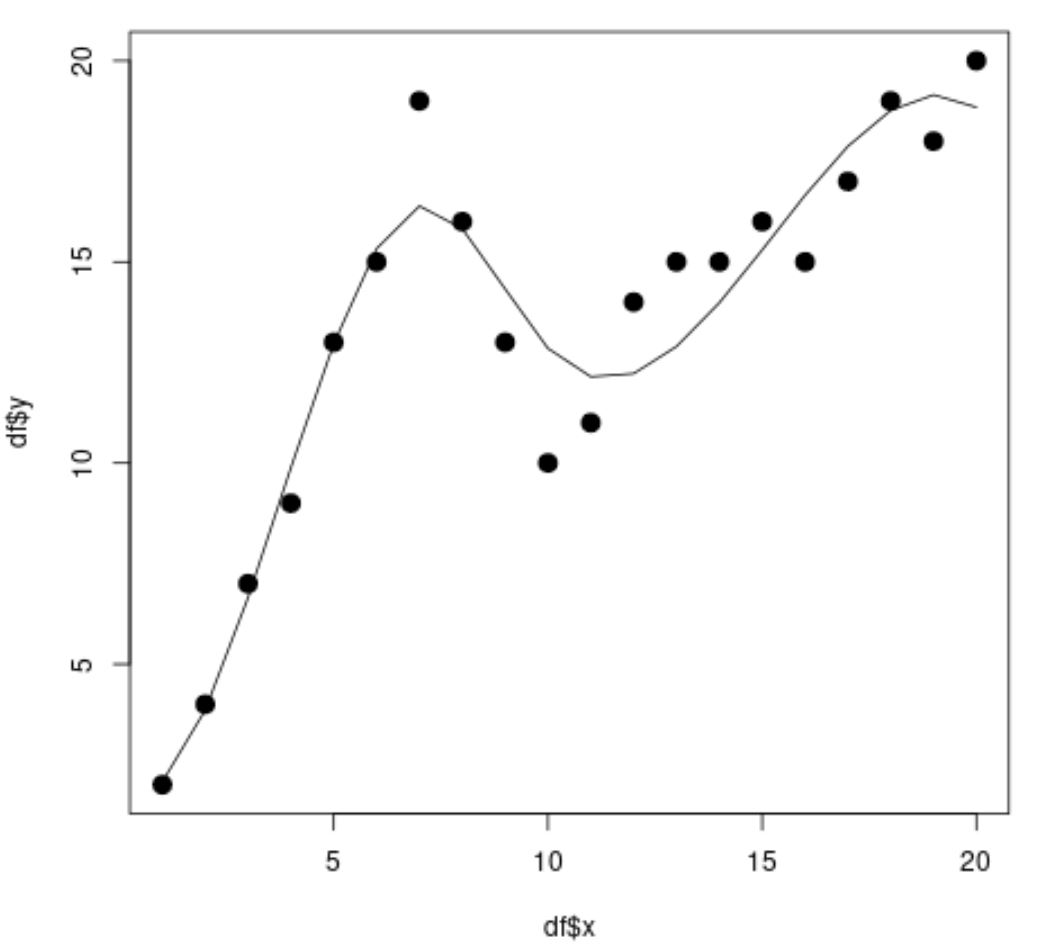
З діаграми розсіювання ми бачимо, що модель сплайн-регресії здатна досить добре підганяти дані.

З результатів моделі ми також бачимо, що скориговане значення R-квадрат становить 0,8987 .

Скориговане значення R-квадрат для цієї моделі набагато вище, ніж для моделі простої лінійної регресії, що говорить нам, що модель сплайн-регресії здатна краще підганяти дані.

Зауважте, що для цього прикладу ми вибрали, щоб вузли були розташовані на x=7 і x=10.

На практиці вам доведеться самостійно вибирати розташування вузлів на основі того, де шаблони даних змінюються, і на основі вашого досвіду домену.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в R:

Як виконати множинну лінійну регресію в R
Як виконати експоненціальну регресію в R
Як виконати зважену регресію найменших квадратів у R