Як створити та інтерпретувати криву roc у stata

Логістична регресія – це статистичний метод, який ми використовуємо для підгонки регресійної моделі, коли змінна відповіді є двійковою. Щоб оцінити, наскільки модель логістичної регресії відповідає набору даних, ми можемо розглянути такі два показники:

• Чутливість: ймовірність того, що модель передбачає позитивний результат для спостереження, коли результат насправді позитивний.
• Специфічність: ймовірність того, що модель передбачає негативний результат для спостереження, коли результат насправді негативний.

Простим способом візуалізації цих двох показників є створення кривої ROC , яка є графіком, що відображає чутливість і специфічність моделі логістичної регресії.

Цей посібник пояснює, як створити та інтерпретувати криву ROC у Stata.

Приклад: крива ROC у Stata

Для цього прикладу ми використаємо набір даних під назвою lbw , який містить такі змінні для 189 матерів:

• низька – незалежно від того, чи має дитина низьку вагу при народженні. 1 = так, 0 = ні.
• вік – вік матері.
• палити – чи курила мати під час вагітності. 1 = так, 0 = ні.

Ми підберемо модель логістичної регресії до даних, використовуючи вік і куріння як пояснювальні змінні та низьку вагу при народженні як змінну відповіді. Далі ми створимо криву ROC, щоб проаналізувати, наскільки модель відповідає даним.

Крок 1: Завантажте та відобразіть дані.

Завантажте дані за допомогою такої команди:

використовуйте https://www.stata-press.com/data/r13/lbw

Отримайте швидке розуміння набору даних за допомогою такої команди:

узагальнити

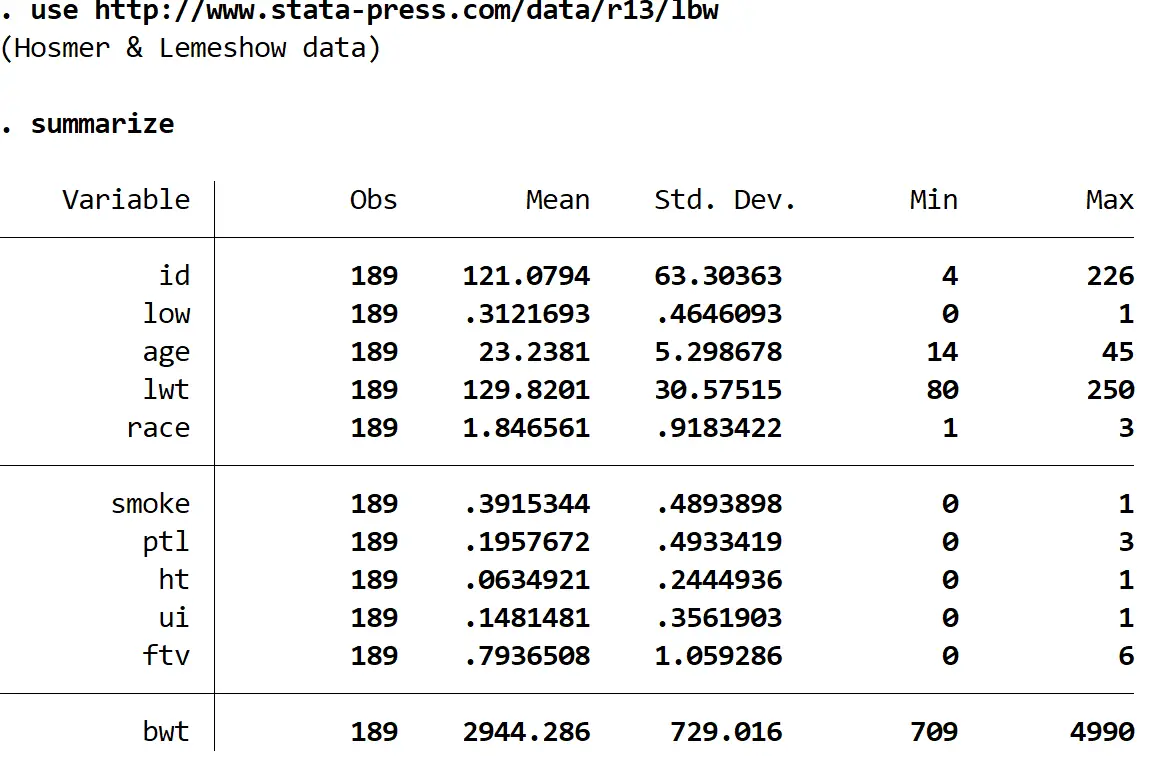
У наборі даних є 11 різних змінних, але нас цікавлять лише три – низький рівень, вік і куріння.

Крок 2. Підберіть модель логістичної регресії.

Використовуйте наступну команду, щоб підібрати модель логістичної регресії:

низький вік диму logit

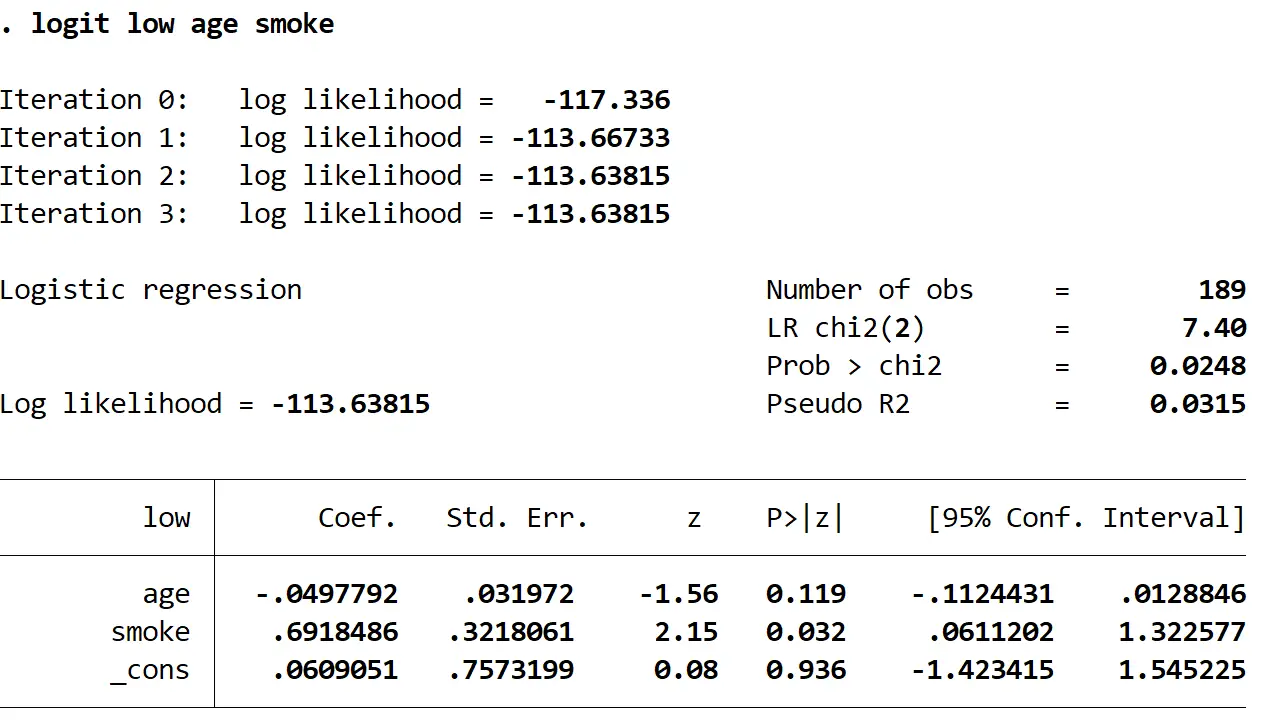
Крок 3: Створіть криву ROC.

Ми можемо створити криву ROC для моделі за допомогою такої команди:

lroc

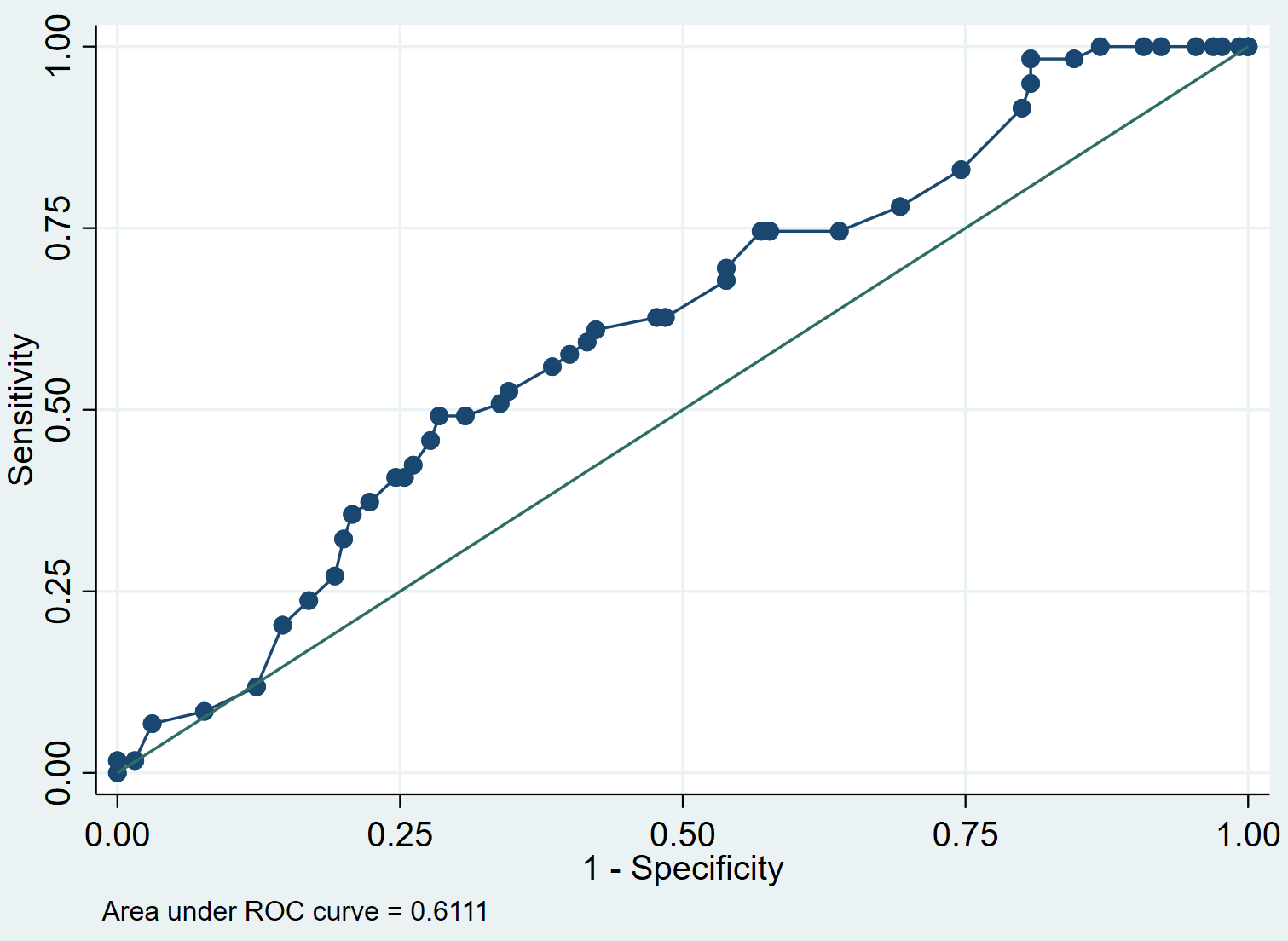
Крок 4: Інтерпретація кривої ROC.

Коли ми підганяємо модель логістичної регресії, її можна використовувати для розрахунку ймовірності того, що дане спостереження матиме позитивний результат, на основі значень змінних-прогнозів.

Щоб визначити, чи слід класифікувати спостереження як позитивне, ми можемо вибрати поріг таким чином, що спостереження зі скоригованою ймовірністю вище порогу класифікуються як позитивні, а всі спостереження зі скоригованою ймовірністю нижче порогу класифікуються як негативні. .

Наприклад, припустімо, що ми вибираємо поріг 0,5. Це означає, що будь-яке спостереження зі скоригованою ймовірністю більше 0,5 матиме позитивний результат, тоді як будь-яке спостереження зі скоригованою ймовірністю менше або дорівнює 0,5 матиме негативний результат.

Крива ROC показує нам значення чутливості проти специфічності 1, коли порогове значення змінюється від 0 до 1. Модель з високою чутливістю та специфічністю матиме криву ROC, яка обіймає верхній лівий кут графіка. Модель з низькою чутливістю та низькою специфічністю матиме криву, близьку до діагоналі 45 градусів.

AUC (площа під кривою) дає нам уявлення про здатність моделі розрізняти позитивні та негативні результати. AUC може коливатися від 0 до 1. Що вищий AUC, то краще модель правильно класифікує результати. У нашому прикладі ми бачимо, що AUC становить 0,6111 .

Ми можемо використовувати AUC для порівняння продуктивності двох або більше моделей. Модель з найвищим AUC працює найкраще.

Додаткові ресурси

Як виконати логістичну регресію в Stata
Як інтерпретувати криву ROC і AUC моделі логістичної регресії