Стандартизація чи нормалізація: в чому різниця?

Стандартизація та нормалізація — це два способи зміни розміру даних.

Нормалізація масштабує набір даних, щоб мати середнє значення 0 і стандартне відхилення 1. Для цього використовується така формула:

x _новий = (x _i – x ) / с

золото:

• x _i : ^i-те значення набору даних
• x : вибірка означає
• s : стандартне відхилення вибірки

Нормалізація змінює розмір набору даних таким чином, щоб кожне значення було між 0 і 1. Це робиться за допомогою такої формули:

x _новий = (x _i – x _min ) / (x _max – x _min )

золото:

• x _i : ^i-те значення набору даних
• x _min : мінімальне значення в наборі даних
• x _max : максимальне значення в наборі даних

Наступні приклади показують, як стандартизувати та нормалізувати набір даних на практиці.

Приклад: як стандартизувати дані

Припустимо, що ми маємо наступний набір даних:

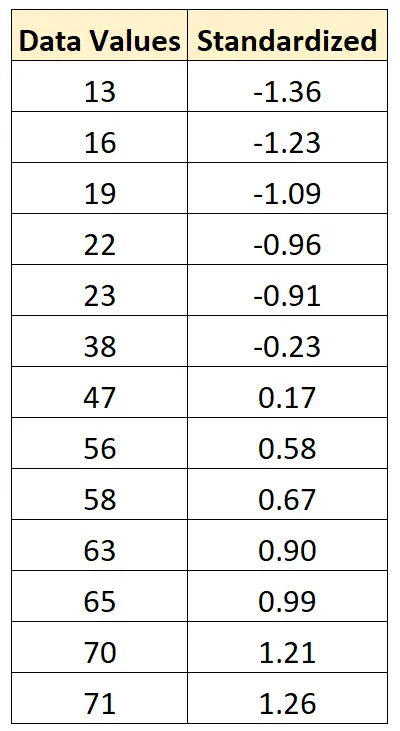
Середнє значення в наборі даних становить 43,15, а стандартне відхилення – 22,13.

Щоб нормалізувати перше значення 13 , ми б застосували формулу, наведену раніше:

• x _новий = (x _i – x ) / s = (13 – 43,15) / 22,13 = -1,36

Щоб нормалізувати друге значення 16 , ми використаємо ту саму формулу:

• x _новий = (x _i – x ) / s = (16 – 43,15) / 22,13 = -1,23

Щоб нормалізувати третє значення 19 , ми використаємо ту саму формулу:

• x _новий = (x _i – x ) / s = (19 – 43,15) / 22,13 = -1,09

Ми можемо використати ту саму формулу для стандартизації кожного значення у вихідному наборі даних:

Приклад: як нормалізувати дані

Знову припустімо, що ми маємо наступний набір даних:

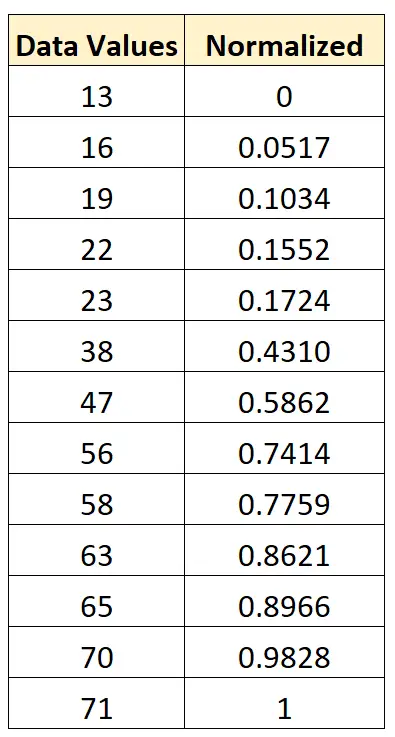
Мінімальне значення в наборі даних – 13, а максимальне – 71.

Щоб нормалізувати перше значення 13 , ми б застосували формулу, наведену раніше:

• x _новий = (x _i – x _min ) / (x _max – x _min ) = (13 – 13) / (71 – 13) = 0

Щоб нормалізувати друге значення 16 , ми використаємо ту саму формулу:

• x _новий = (x _i – x _min ) / (x _max – x _min ) = (16 – 13) / (71 – 13) = 0,0517

Щоб нормалізувати третє значення 19 , ми використаємо ту саму формулу:

• x _новий = (x _i – x _min ) / (x _max – x _min ) = (19 – 13) / (71 – 13) = 0,1034

Ми можемо використати ту саму формулу, щоб нормалізувати кожне значення у вихідному наборі даних між 0 і 1:

Стандартизація чи нормалізація: коли їх використовувати?

Як правило, ми нормалізуємо дані, коли робимо якийсь тип аналізу, у якому ми маємо кілька змінних, виміряних у різних масштабах, і ми хочемо, щоб кожна зі змінних мала однаковий діапазон.

Це запобігає надмірному впливу однієї змінної, особливо якщо вона вимірюється в різних одиницях (тобто якщо одна змінна вимірюється в дюймах, а інша – у ярдах).

З іншого боку, ми зазвичай нормалізуємо дані, коли хочемо знати, скільки стандартних відхилень має кожне значення в наборі даних від середнього.

Наприклад, у нас може бути список екзаменаційних балів для 500 учнів певної школи, і ми хотіли б знати, на скільки стандартних відхилень кожен екзаменаційний бал від середнього балу.

У цьому випадку ми могли б нормалізувати необроблені дані, щоб отримати цю інформацію. Тоді стандартизований бал 1,26 скаже нам, що іспитовий бал цього конкретного студента на 1,26 стандартного відхилення перевищує середній іспитовий бал.

Якщо ви вирішите нормалізувати або стандартизувати свої дані, майте на увазі наступне:

• Нормалізований набір даних завжди матиме значення від 0 до 1.
• Стандартизований набір даних матиме середнє значення 0 і стандартне відхилення 1, але немає конкретної верхньої чи нижньої межі для максимальних і мінімальних значень.

Залежно від конкретного сценарію, може бути доцільніше нормалізувати або стандартизувати дані.

Додаткові ресурси

У наступних посібниках пояснюється, як стандартизувати та нормалізувати дані в різних статистичних програмах:

Як нормалізувати дані в R
Як нормалізувати дані в Excel
Як нормалізувати дані в Python
Як стандартизувати дані в R