Що таке стандартизовані залишки?

Залишок — це різниця між спостережуваним значенням і прогнозованим значенням у регресійній моделі .

Він розраховується таким чином:

Залишок = спостережуване значення – прогнозоване значення

Якщо ми побудуємо спостережувані значення та накладемо підібрану лінію регресії, залишки для кожного спостереження будуть вертикальною відстанню між спостереженням і лінією регресії:

Один тип залишку, який ми часто використовуємо для визначення викидів у регресійній моделі, називається стандартизованим залишком .

Він розраховується таким чином:

r _i = e _i / s(e _i ) = e _i / RSE√ 1-h _ii

золото:

• e _i : i- ^й залишок
• RSE: залишкова стандартна помилка моделі
• h _ii : Зростання ^i-го спостереження

На практиці ми часто розглядаємо будь-який стандартизований залишок, абсолютне значення якого перевищує 3, як викид.

Це не обов’язково означає, що ми видалимо ці спостереження з моделі, але ми повинні принаймні вивчити їх далі, щоб переконатися, що вони не є результатом помилки введення даних або якоїсь іншої дивної події.

Примітка. Іноді стандартизовані залишки також називають «залишками, дослідженими всередині підприємства».

Приклад: як розрахувати стандартизовані залишки

Припустімо, що ми маємо наступний набір даних із загалом 12 спостереженнями:

Якщо ми використовуємо статистичне програмне забезпечення (наприклад, R , Excel , Python , Stata тощо), щоб підібрати лінію лінійної регресії до цього набору даних, ми побачимо, що лінія найкращого підходу виявляється:

y = 29,63 + 0,7553x

Використовуючи цей рядок, ми можемо обчислити прогнозоване значення для кожного значення Y на основі значення X. Наприклад, прогнозоване значення першого спостереження буде таким:

y = 29,63 + 0,7553*(8) = 35,67

Тоді ми можемо обчислити нев’язку для цього спостереження наступним чином:

Залишок = спостережуване значення – прогнозоване значення = 41 – 35,67 = 5,33

Ми можемо повторити цей процес, щоб знайти нев’язку для кожного спостереження:

Ми також можемо використати статистичне програмне забезпечення, щоб визначити, що залишкова стандартна помилка моделі становить 4,44 .

І хоча це виходить за рамки цього підручника, ми можемо використовувати програмне забезпечення, щоб знайти статистику кредитного плеча (h _ii ) для кожного спостереження:

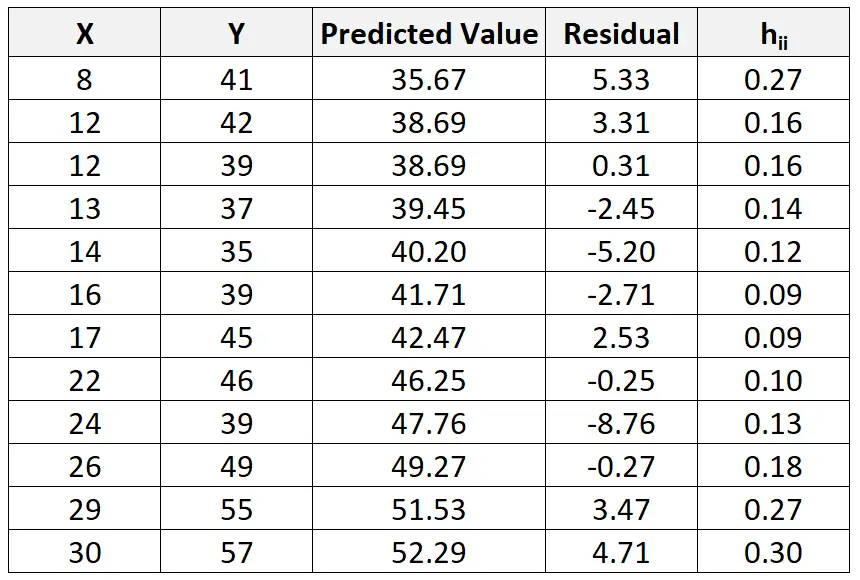
Тоді ми можемо використати наступну формулу для розрахунку стандартизованої нев’язки для кожного спостереження:

r _i = e _i / RSE√ 1-h _ii

Наприклад, стандартизований залишок для першого спостереження обчислюється наступним чином:

r _i = 5,33 / 4,44√ 1-0,27 = 1,404

Ми можемо повторити цей процес, щоб знайти стандартизований залишок для кожного спостереження:

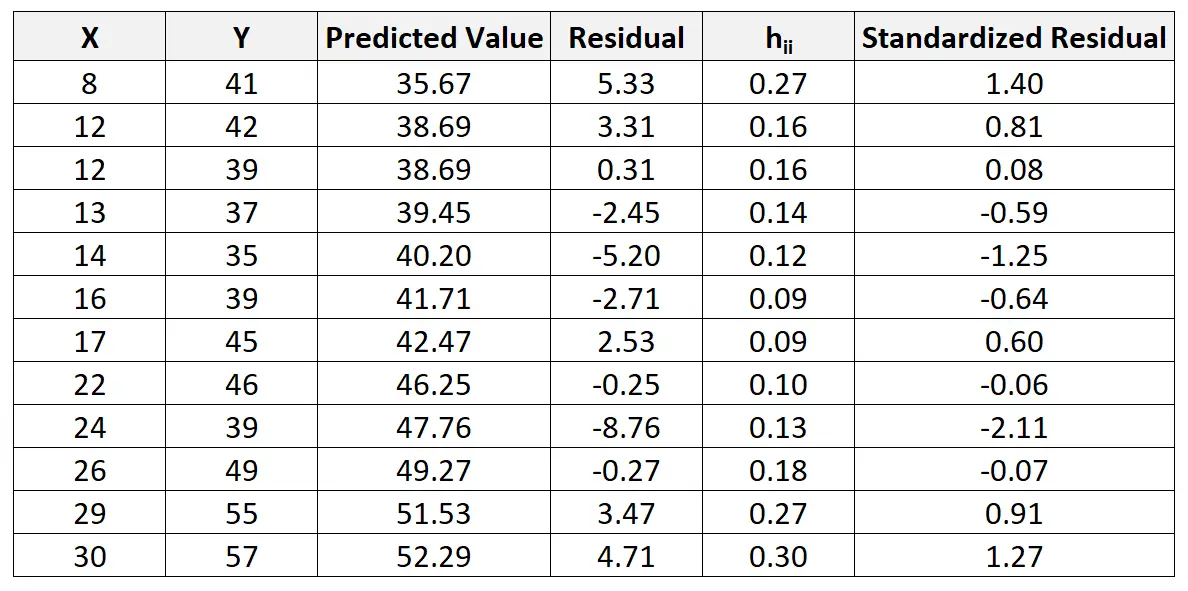
Потім ми можемо створити швидку діаграму розсіювання прогнозованих значень проти стандартизованих залишків, щоб візуально побачити, чи будь-який із стандартизованих залишків перевищує абсолютний поріг значення 3:

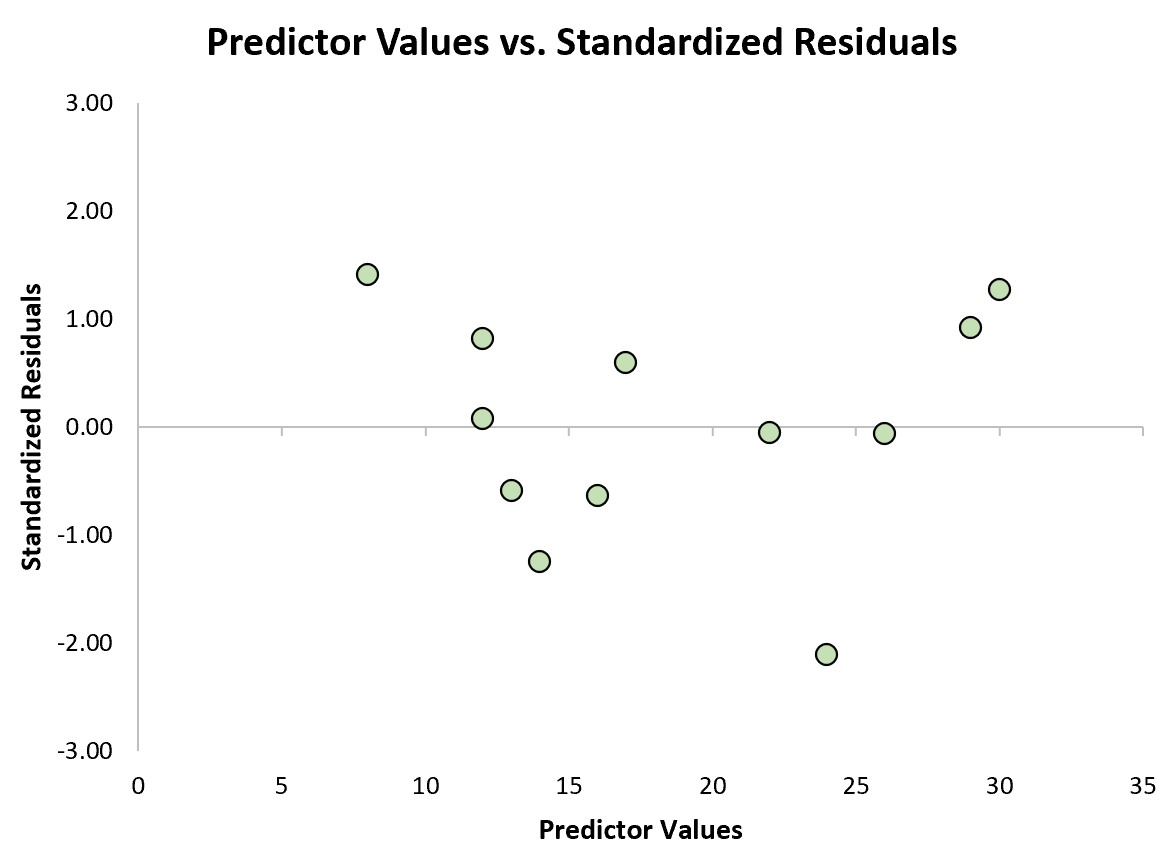
З графіка ми бачимо, що жоден із стандартизованих залишків не перевищує абсолютного значення 3. Таким чином, жодне зі спостережень не виглядає викидом.

Слід зазначити, що в деяких випадках дослідники вважають спостереження, стандартизовані залишки яких перевищують абсолютне значення 2, викидами.

Залежно від сфери, в якій ви працюєте, і конкретної проблеми, над якою ви працюєте, ви вирішуєте, чи бажаєте ви використовувати абсолютне значення 2 чи 3 як порогове значення для викидів.

Додаткові ресурси

Наступні посібники надають додаткову інформацію про стандартизовані залишки:

Що таке залишки в статистиці?
Як розрахувати стандартизовані залишки в Excel
Як обчислити стандартизовані залишки в R
Як обчислити стандартизовані залишки в Python