Розуміння стандартної похибки нахилу регресії

Стандартна помилка нахилу регресії — це спосіб вимірювання «невизначеності» в оцінці нахилу регресії.

Він розраховується таким чином:

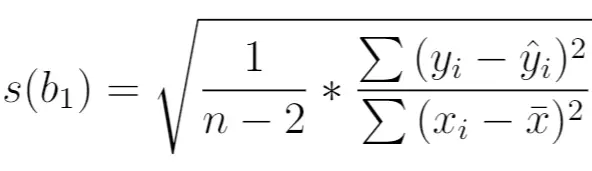
золото:

• n : загальний розмір вибірки
• y _i : реальне значення змінної відповіді
• ŷ _i : прогнозоване значення змінної відповіді
• x _i : реальне значення прогнозної змінної
• x̄ : середнє значення прогнозної змінної

Чим менша стандартна помилка, тим менша мінливість навколо оцінки коефіцієнта для нахилу регресії.

Стандартна помилка нахилу регресії відображатиметься у стовпці «стандартна помилка» у вихідних даних регресії більшості статистичних програм:

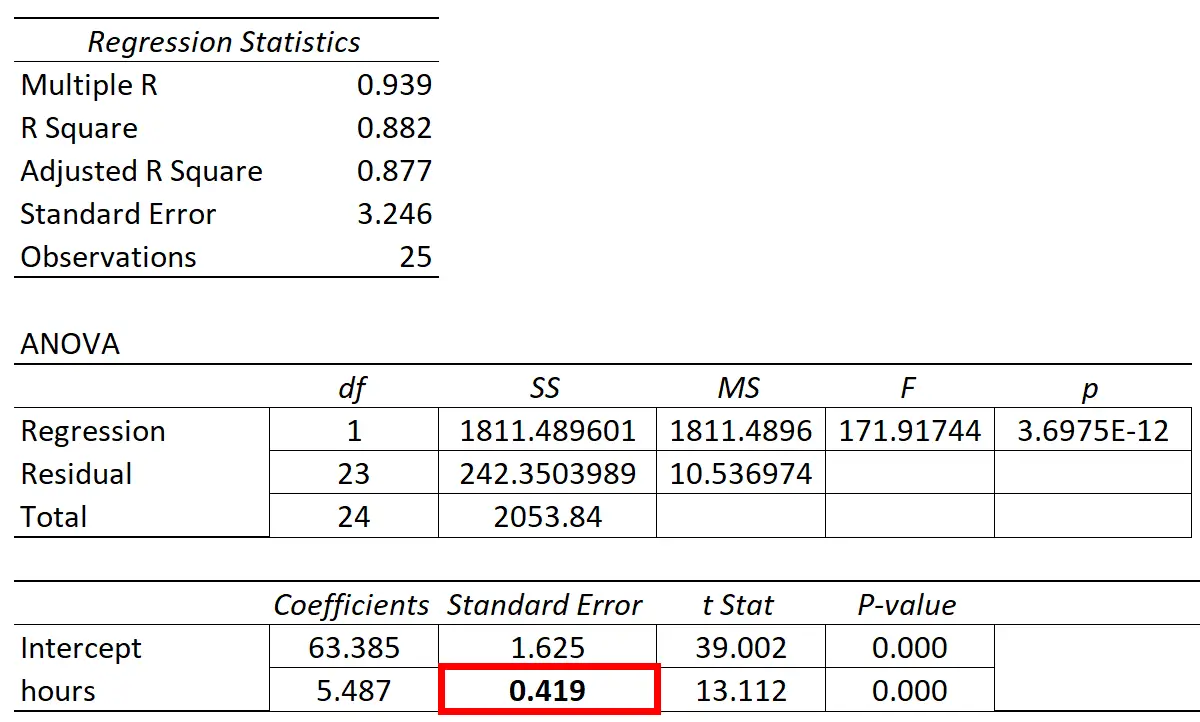
У наведених нижче прикладах показано, як інтерпретувати стандартну помилку нахилу регресії в двох різних сценаріях.

Приклад 1: Інтерпретація малої стандартної похибки нахилу регресії

Припустімо, професор хоче зрозуміти залежність між кількістю вивчених годин і підсумковою іспитовою оцінкою студентів його класу.

Він збирає дані для 25 студентів і створює таку діаграму розсіювання:

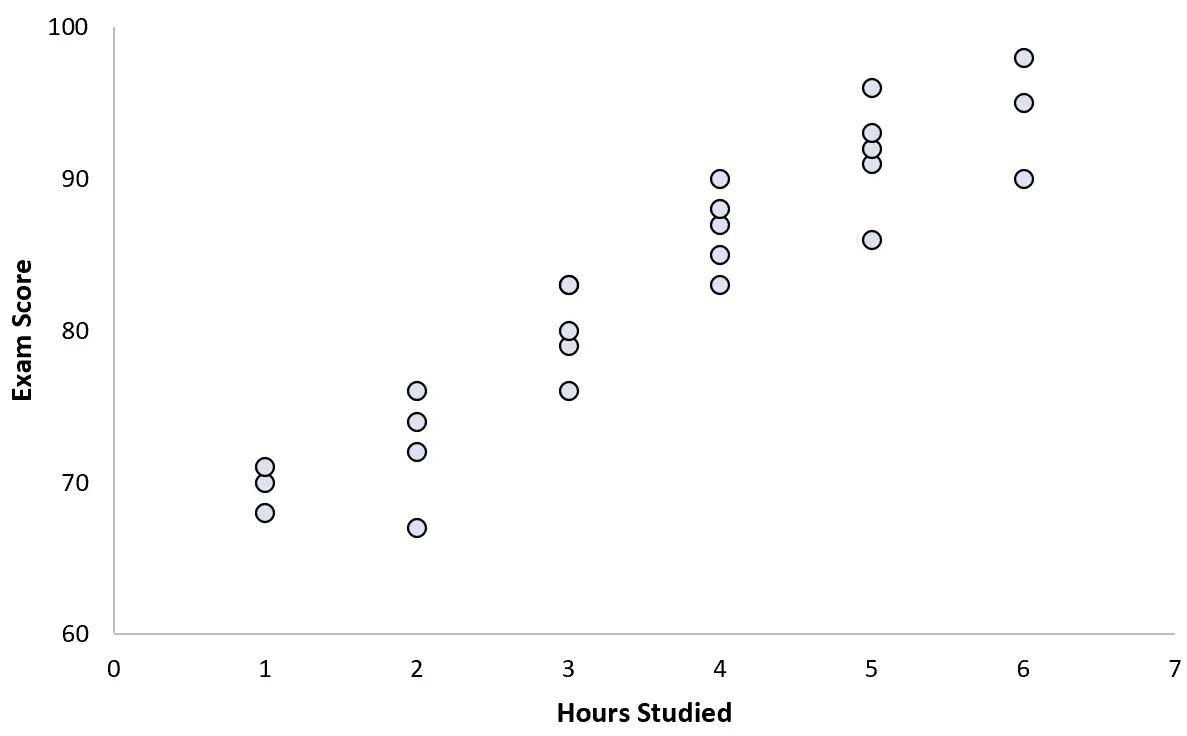
Існує явно позитивний зв’язок між двома змінними. Зі збільшенням кількості годин, які вивчаються, оцінка за іспит зростає досить передбачуваною швидкістю.

Потім він склав просту модель лінійної регресії, використовуючи вивчені години як прогностичну змінну та оцінку підсумкового іспиту як змінну відповіді.

У наступній таблиці показано результати регресії:

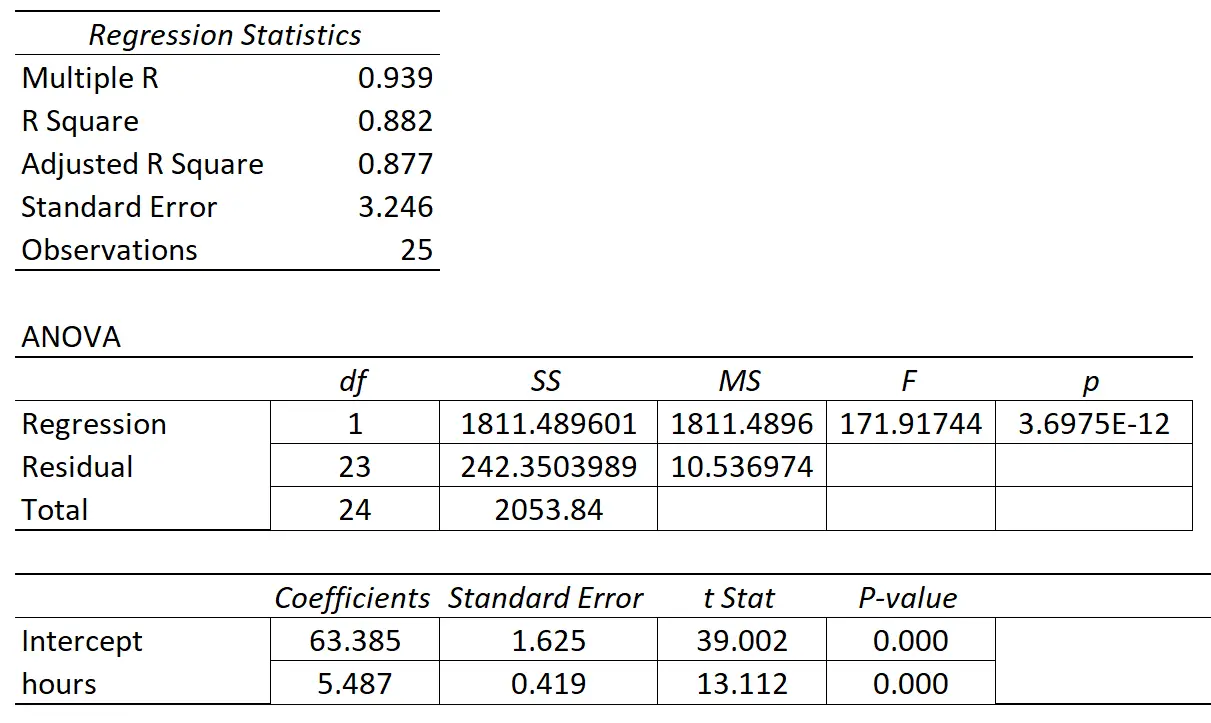
Коефіцієнт предикторної змінної «годин навчання» становить 5,487. Це говорить нам про те, що кожна додаткова вивчена година пов’язана із середнім підвищенням оцінки за іспит на 5487 .

Стандартна помилка становить 0,419 , що являє собою міру мінливості навколо цієї оцінки для нахилу регресії.

Ми можемо використати це значення для розрахунку t-статистики для змінної предиктора «годин навчання»:

• t статистика = оцінка коефіцієнта / стандартна помилка
• t-статистика = 5,487 / 0,419
• t-статистика = 13,112

P-значення, яке відповідає цій тестовій статистиці, становить 0,000, що вказує на те, що «вивчені години» мають статистично значущий зв’язок із підсумковою оцінкою іспиту.

Оскільки стандартна помилка нахилу регресії була малою порівняно з оцінкою коефіцієнта нахилу регресії, змінна предиктора була статистично значущою.

Приклад 2: Інтерпретація великої стандартної похибки нахилу регресії

Припустімо, що інший професор хоче зрозуміти зв’язок між кількістю вивчених годин і підсумковою іспитовою оцінкою студентів його класу.

Вона збирає дані для 25 студентів і створює таку діаграму розсіювання:

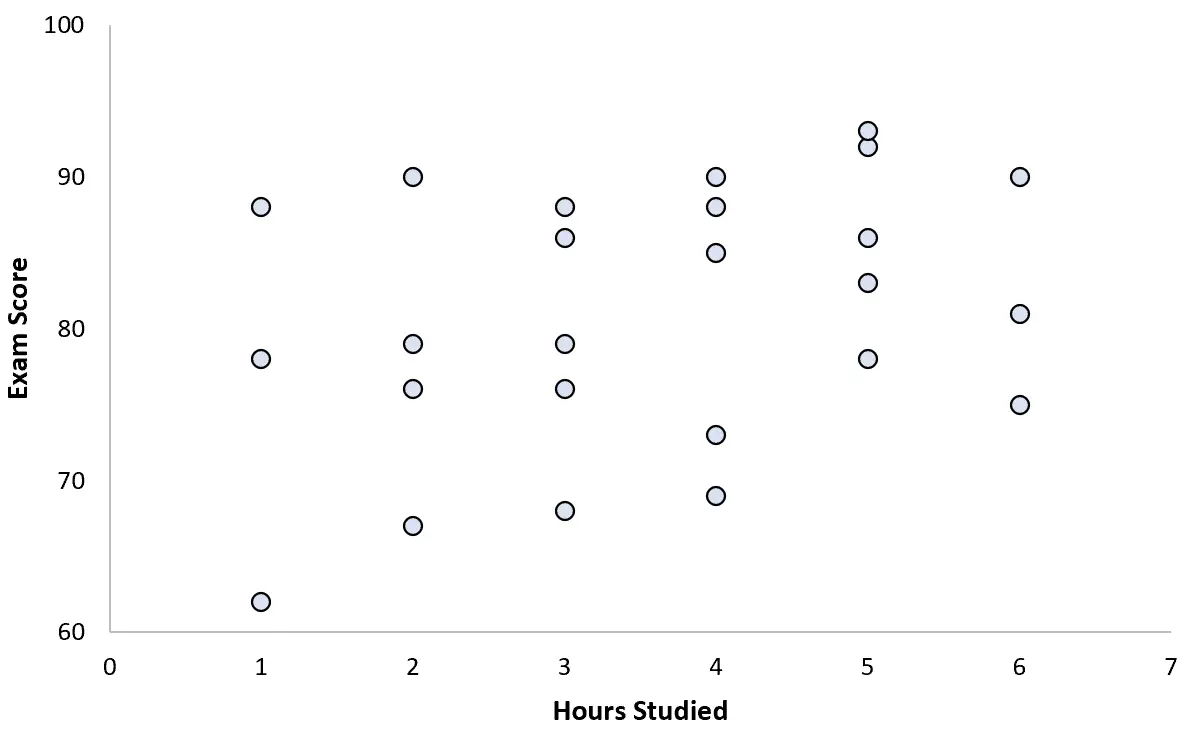
Здається, між двома змінними існує невеликий позитивний зв’язок. Зі збільшенням кількості годин навчання оцінка за іспит зазвичай зростає, але не передбачуваною швидкістю.

Припустімо, що потім професор укладає просту модель лінійної регресії, використовуючи вивчені години як змінну прогностичну величину та оцінку підсумкового іспиту як змінну відповіді.

У наступній таблиці показано результати регресії:

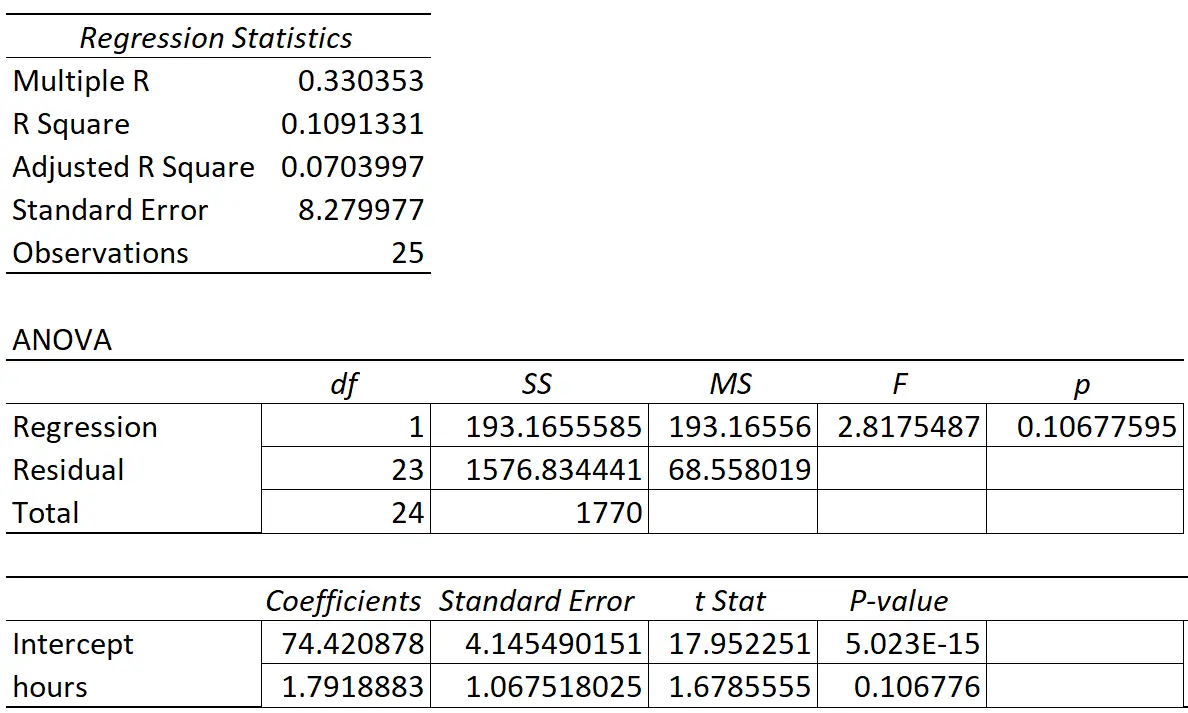
Коефіцієнт предикторної змінної «годин навчання» становить 1,7919. Це говорить нам про те, що кожна додаткова вивчена година пов’язана із середнім збільшенням оцінки іспиту на 1,7919 .

Стандартна помилка становить 1,0675 , що є мірою мінливості навколо цієї оцінки для нахилу регресії.

Ми можемо використати це значення для розрахунку t-статистики для змінної предиктора «годин навчання»:

• t статистика = оцінка коефіцієнта / стандартна помилка
• t-статистика = 1,7919 / 1,0675
• t-статистика = 1,678

P-значення, яке відповідає цій тестовій статистиці, становить 0,107. Оскільки це p-значення не менше 0,05, це вказує на те, що «вивчені години» не мають статистично значущого зв’язку з оцінкою підсумкового іспиту.

Оскільки стандартна помилка нахилу регресії була великою відносно оцінки коефіцієнта нахилу регресії, змінна предиктора не була статистично значущою.

Додаткові ресурси

Вступ до простої лінійної регресії
Вступ до множинної лінійної регресії
Як читати та інтерпретувати таблицю регресії