Як оцінити стандартне відхилення будь-якої гістограми

Гістограма надає корисний спосіб візуалізації розподілу значень у наборі даних.

Вісь абсцис гістограми відображає групи значень даних, а вісь у говорить нам, скільки спостережень у наборі даних міститься в кожній групі.

Оскільки гістограма розміщує спостереження в біни, неможливо обчислити точне стандартне відхилення набору даних, представленого гістограмою, але можна оцінити стандартне відхилення.

У наступному прикладі показано, як це зробити.

Пов’язане: Як оцінити середнє та медіану будь-якої гістограми

Як оцінити стандартне відхилення гістограми

Щоб оцінити стандартне відхилення гістограми, ви повинні спочатку оцінити середнє значення.

Ми можемо використати наступну формулу для оцінки середнього:

Середнє значення: Σm _i n _i / N

золото:

• m _i : середина i- ^го бункера
• n _i : частота i ^-го діапазону
• N: Загальний розмір вибірки

Наприклад, припустимо, що ми маємо наступну гістограму:

Ось як оцінити середнє значення цієї гістограми:

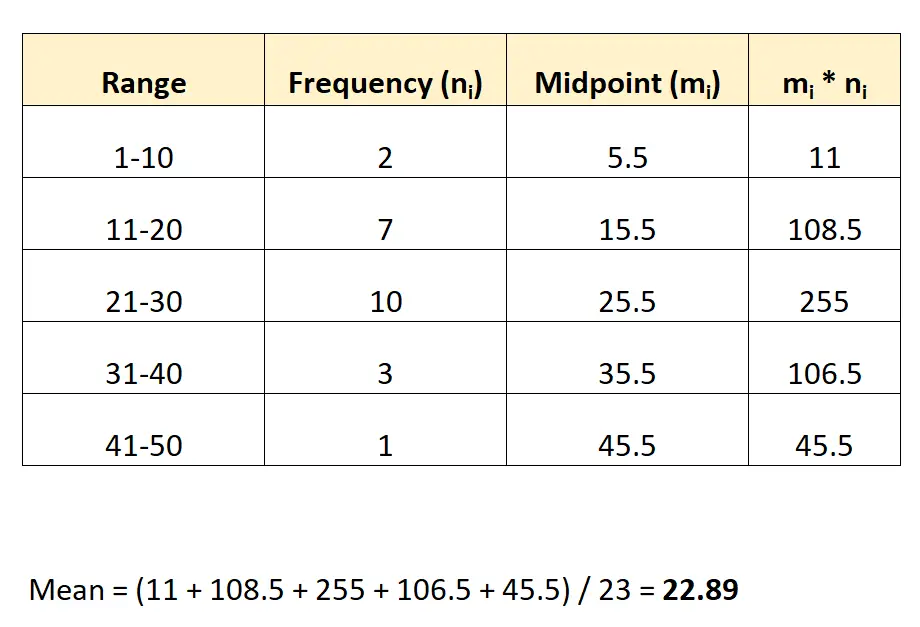
Ми оцінюємо середній показник у 22,89 .

Примітка. Середню точку кожної групи можна знайти, взявши середнє значення нижнього та верхнього значень діапазону. Наприклад, середня точка першої групи обчислюється так: (1+10) / 2 = 5,5.

Тепер, коли ми маємо оцінку середнього значення, ми можемо використати таку формулу для оцінки стандартного відхилення:

Стандартне відхилення: √ Σn _i (m _i -μ) ² / (N-1)

золото:

• n _i : частота i ^-го діапазону
• m _i : середина i- ^го бункера
• μ : середнє значення
• N: Загальний розмір вибірки

Ось як ми можемо застосувати цю формулу до нашого набору даних:

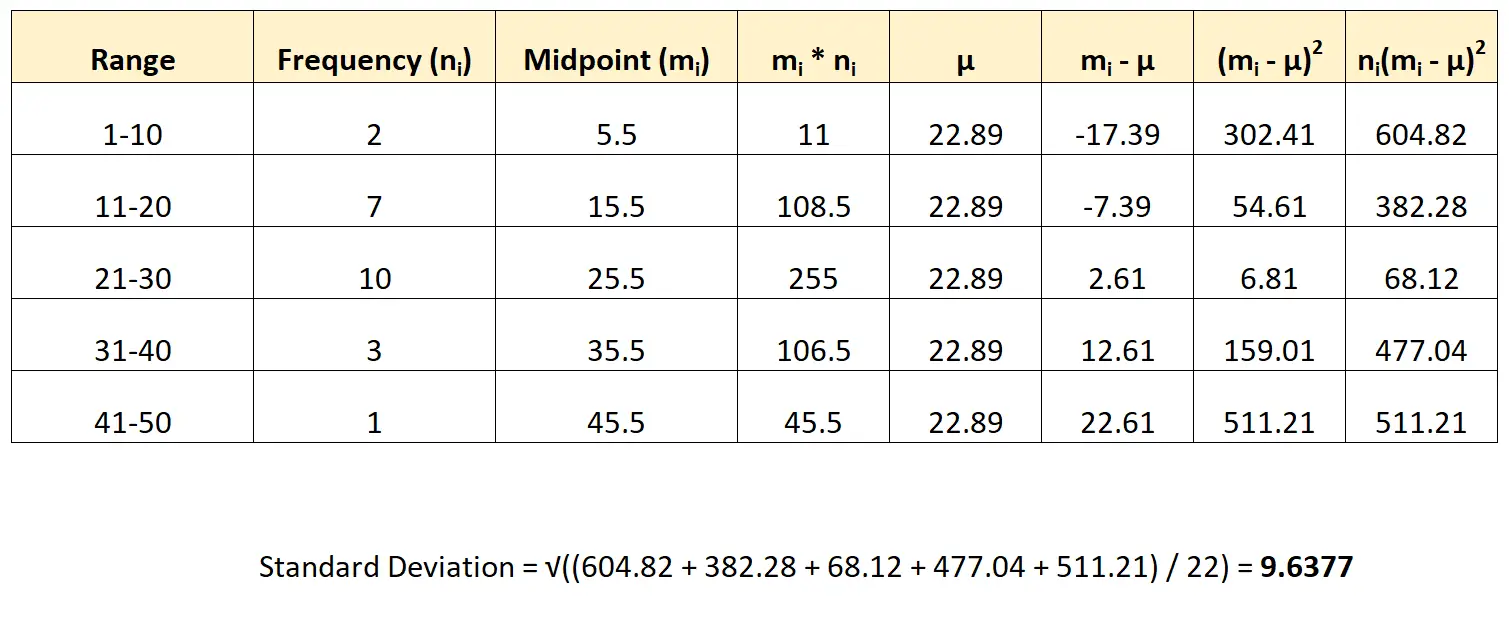Ми оцінюємо стандартне відхилення набору даних у 9,6377 .

Хоча не гарантовано, що він точно відповідає стандартному відхиленню набору даних (оскільки ми не знаємовихідних значень даних у наборі даних), він представляє нашу найкращу оцінку стандартного відхилення.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання, пов’язані з даними, згрупованими в групи:

Як знайти дисперсію згрупованих даних
Як знайти медіану згрупованих даних
Як знайти режим згрупованих даних