Як інтерпретувати стандартне відхилення нуля

У статистиці стандартне відхилення використовується для вимірювання розподілу значень у вибірці.

Ми можемо використати таку формулу, щоб обчислити стандартне відхилення заданої вибірки:

√ Σ(x _i – x _bar ) ² / (n-1)

золото:

• Σ: символ, що означає «сума»
• x _i : ^i-те значення вибірки
• x _бар : Зразок означає
• n: розмір вибірки

Чим вище значення стандартного відхилення, тим більше розсіяні значення у вибірці .

Чим нижче значення стандартного відхилення, тим тісніше згруповані значення.

Якщо стандартне відхилення вибірки дорівнює нулю, це означає, що всі значення у вибірці абсолютно однакові.

Іншими словами, між значеннями немає розриву.

У наступному прикладі показано, як інтерпретувати стандартне відхилення нуля на практиці.

Приклад: як інтерпретувати стандартне відхилення нуля

Припустимо, ми збираємо просту випадкову вибірку з 10 ящірок і вимірюємо їхню довжину (у дюймах):

Довжина : 7, 7, 7, 7, 7, 7, 7, 7, 7, 7

Середня довжина ящірок у зразку становить 7 дюймів.

Знаючи це, ми можемо обчислити вибіркове стандартне відхилення для цього набору даних:

• s = √ Σ(x _i – x _bar ) ² / (n-1)
• s = √ ((7 – 7) ² + (7 – 7) ² + (7 – 7) ² + … + (7 – 7) ² / (10-1)
• s = √ 0 ² + 0 ² + 0 ² + … + 0 ² / 9
• s = 0

Вибіркове стандартне відхилення виявляється рівним 0 .

Оскільки кожна ящірка має однакову довжину, розподіл значень у наборі даних точно дорівнює нулю.

Чи дорівнюватиме колись стандартне відхилення нулю в реальному світі?

Цілком можливо, що стандартне відхилення реального набору даних дорівнює нулю, але це рідко.

Найвірогіднішим сценарієм, коли ви можете зіткнутися зі стандартним відхиленням нуль, буде збір невеликих вибірок для рідкісних подій.

Наприклад, припустімо, що ви збираєте дані про кількість дорожньо-транспортних пригод за один тиждень у певному місті.

Цілком можливо, що ви збираєте такі дані:

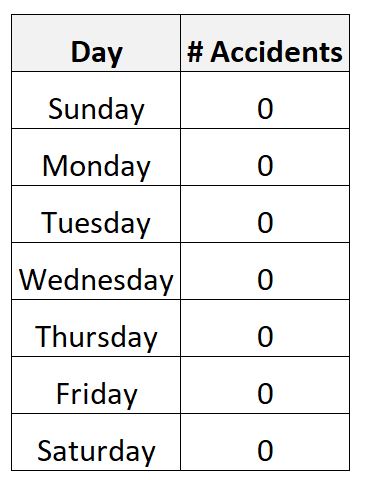
У цьому сценарії середня кількість щоденних аварій буде дорівнювати нулю, і стандартне відхилення також дорівнюватиме нулю.

Або, можливо, ви збираєте такі дані про кількість місячних продажів дорогого продукту для бізнесу за 6-місячний період:

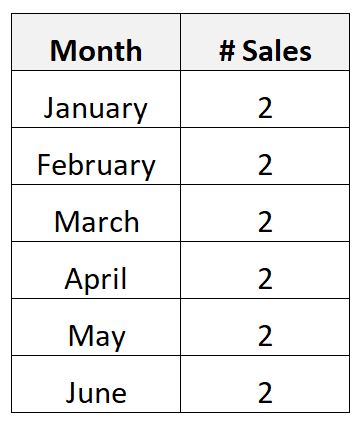
Оскільки продукт дуже дорогий, виявляється, що компанія продає лише два на місяць.

У цьому сценарії середня кількість проданих продуктів за місяць дорівнює двом, а стандартне відхилення проданих продуктів за місяць дорівнює нулю.

Щоразу, коли ви стикаєтеся зі стандартним відхиленням нуля в реальному наборі даних, просто знайте, що це означає, що кожне значення в наборі даних абсолютно однакове.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про стандартне відхилення в статистиці:

Чому стандартне відхилення важливе?
Стандартне відхилення та стандартна помилка: у чому різниця?
Стандартне відхилення та інтерквартильний діапазон: у чому різниця?