Socs: корисна абревіатура для опису дистрибутивів

У статистиці ми часто хочемо зрозуміти, як розподіляється набір даних. Зокрема, є чотири речі, які корисно знати про розподіл:

1 . Форма

• Розподіл симетричний чи зміщений в одну сторону?
• Розподіл унімодальний (один пік) чи бімодальний (два піки)?

2. Викиди

• Чи є в розподілі викиди?

3. Центр

• Що таке середнє, медіана та спосіб розподілу?

4. Поширення

• Що таке діапазон, інтерквартильний діапазон, стандартне відхилення та дисперсія розподілу?

SOCS — це корисна абревіатура, яку ми можемо використовувати, щоб запам’ятати ці чотири речі. Це означає «форма, викиди, центр, поширення».

Давайте розглянемо простий приклад того, як використовувати SOCS для опису розподілу.

Приклад: як використовувати SOCS для опису розподілу

Скажімо, у нас є наступний набір даних, який показує висоту зразка з 20 різних рослин.

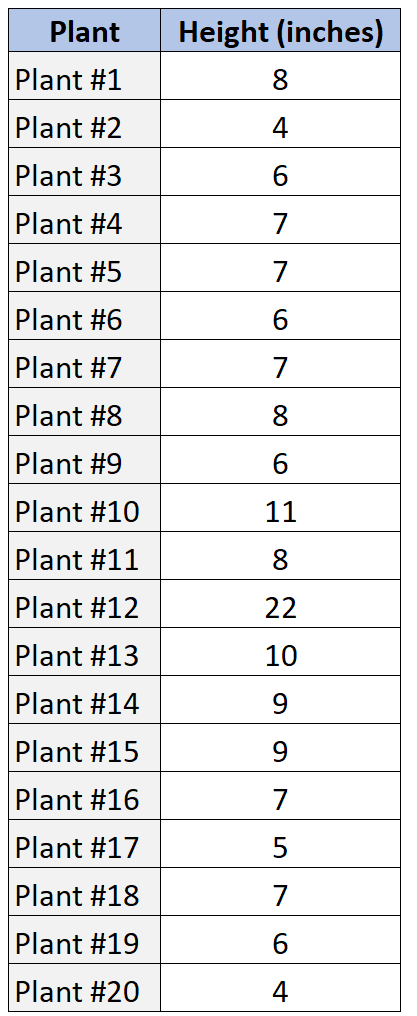
Ось як ми можемо використовувати SOCS для опису цього розподілу значень даних.

Форма

Спочатку ми хочемо описати форму розподілу.

Корисним способом візуалізації форми розподілу є створення гістограми, яка відображає частоти кожного значення в наборі даних:

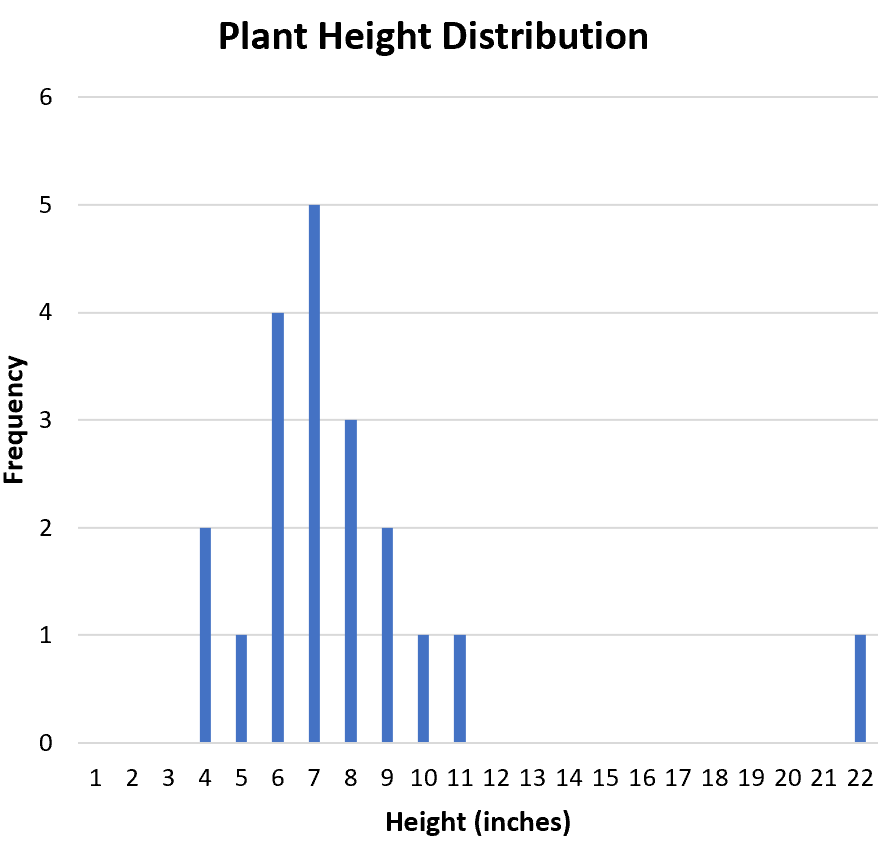
Розподіл симетричний чи зміщений в одну сторону?   З гістограми видно, що розподіл приблизно симетричний. Іншими словами, значення не є упередженими в ту чи іншу сторону.

Розподіл унімодальний (один пік) чи бімодальний (два піки)? Розподіл унімодальний. Він має пік при значенні «7».

Викиди

Далі ми хочемо визначити, чи є в наборі даних викиди. З гістограми ми можемо візуально перевірити розподіл і побачити, що 22 потенційно є викидом:

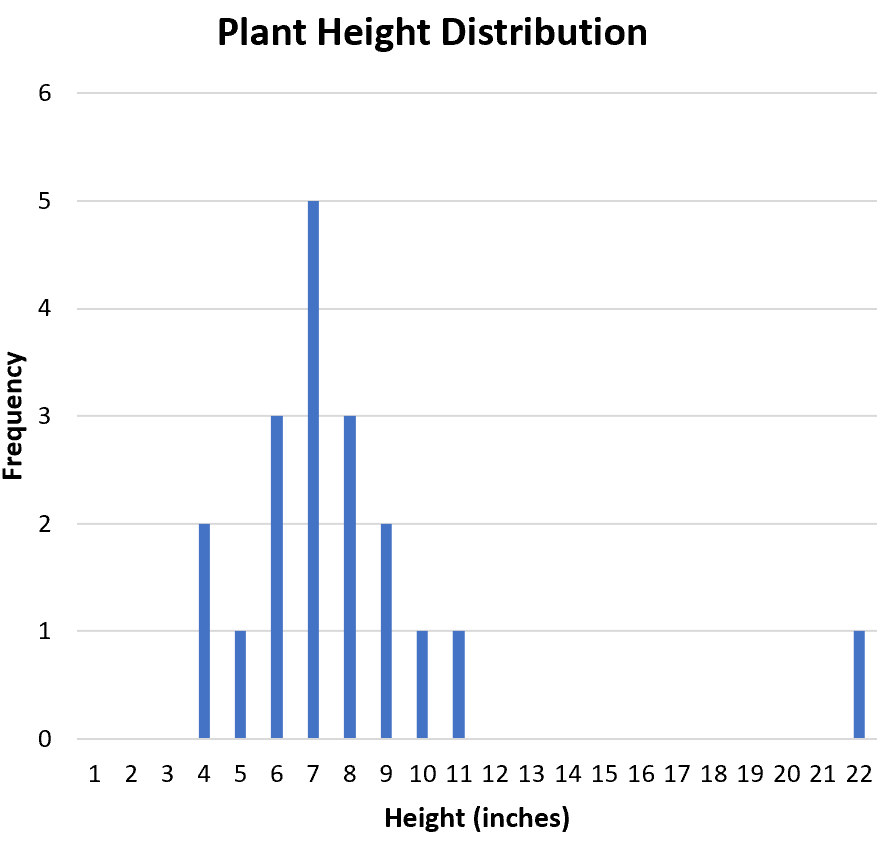
Поширеним способом формального визначення викиду є будь-яке значення, яке в 1,5 рази перевищує інтерквартильний діапазон вище третього квартиля або нижче першого квартиля.

Використовуючи калькулятор міжквартильного діапазону, ми можемо ввести 20 значень необроблених даних і побачити, що третій квартиль дорівнює 9 , інтерквартильний діапазон дорівнює 3 , і тому будь-яке значення, яке перевищує 9 + (1,5*3) = 13,5 , є викидом, за визначенням .

Оскільки 22 більше за 13,5, ми можемо оголосити 22 викидом.

центр

Потім ми хочемо описати, де знаходиться центр розподілу. Три загальні міри центральної тенденції , які ми можемо використовувати, це середнє, медіана та мода.

Середнє значення: це середнє значення розподілу. Ми знаходимо це шляхом додавання всіх окремих значень, а потім розділення на загальну кількість значень:

Середнє = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7,85

Медіана: це «середнє» значення розподілу. Ми знаходимо це, впорядковуючи всі значення від найменшого до найбільшого, а потім визначаючи середнє значення. Виходить 7 .

4, 4, 5, 6, 6, 6, 6, 7, 7, 7, 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22

Режим: це значення, яке з’являється найчастіше. Виходить 7 .

Поширення

Далі ми хочемо описати розподіл значень у розподілі. Чотири загальні міри дисперсії, які ми можемо використовувати, це діапазон, інтеркварільний діапазон, стандартне відхилення та дисперсія.

Діапазон: це різниця між найбільшим і найменшим значенням у наборі даних. Це виходить 22 – 4 = 18 .

Міжквартильний діапазон: вимірює ширину середніх 50% значень даних. Ввівши 20 необроблених значень даних у калькулятор інтерквартильного діапазону, ми побачимо, що це дорівнює 3 .

Стандартне відхилення: це показник середнього розподілу значень даних. Ввівши 20 необроблених значень даних у калькулятор дисперсії та стандартного відхилення, ми побачимо, що стандартне відхилення дорівнює 3,69 .

Дисперсія: це просто стандартне відхилення в квадраті. Це дорівнює 3,69 ² = 13,63 .

Висновок

Використовуючи SOCS як орієнтир, ми змогли описати розподіл рослин по висоті таким чином:

• Розподіл був унімодальним і симетричним, тобто мав лише один пік і не був перекошеним в одну чи іншу сторону.
• Розподіл мав один викид: 22.
• Розподіл мав середнє значення 7,85, медіану 7 і моду 7.
• Розподіл мав діапазон 18, інтерквартильний діапазон 3, стандартне відхилення 3,69 і дисперсію 13,63.

Зверніть увагу, що ми можемо використовувати SOCS для опису будь-якого розподілу, що є корисним способом для нас, щоб повністю зрозуміти форму розподілу, чи є в ньому викиди, де приблизно знаходиться центр і як розподілити значення даних. є.