Рейтинг (статистика)

У цій статті ми пояснюємо, що таке діапазон у статистиці та як він обчислюється. Ви знайдете розв’язану вправу щодо обсягу набору даних і, нарешті, ми покажемо вам, для чого він призначений і коли його слід використовувати.

Що таке діапазон у статистиці?

У статистиці діапазон — це міра дисперсії, яка вказує різницю між максимальним значенням і мінімальним значенням даних вибірки. Таким чином, щоб обчислити обсяг генеральної сукупності або статистичної вибірки, максимальне значення необхідно відняти від мінімального значення.

Наприклад, якщо максимальне значення набору даних дорівнює 9, а мінімальне значення – 2, діапазон цієї статистичної вибірки дорівнює 7 (9-2=7).

Статистичний діапазон також називають екстентом або діапазоном вимірювання.

Отже, діапазон — це міра дисперсії з дисперсією, стандартним відхиленням (або стандартним відхиленням), середнім відхиленням і коефіцієнтом варіації.

Як розрахувати діапазон у статистиці

Діапазон вибірки обчислюється шляхом віднімання екстремальних значень даних статистичної вибірки, тобто діапазон вибірки дорівнює максимальному значенню всіх даних мінус мінімальне значення .

Таким чином, формула для обчислення статистичного діапазону набору даних виглядає так:

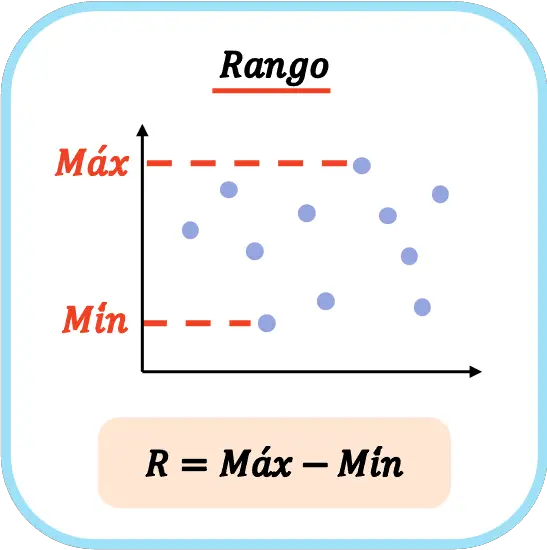
У статистиці символ великої літери R часто використовується для позначення обсягу ряду даних.

Тому розрахувати діапазон набору даних досить просто, оскільки вам просто потрібно визначити різницю між крайніми значеннями. Єдине, на що вам потрібно звернути увагу, це правильно визначити максимальні та мінімальні дані та не забувати жодних цифр.

Приклад діапазону (статистика)

Ознайомившись із визначенням діапазону в статистиці, нижче наведено робочий приклад, щоб ви могли побачити, як отримується діапазон набору даних.

• Компанія хоче статистично проаналізувати продажі свого флагманського продукту за останні двадцять років. Для цього вони просять обчислити кілька статистичних показників, у тому числі рейтинг. Якщо продажі продукту такі, як показано в наступній таблиці, який діапазон цього набору даних?

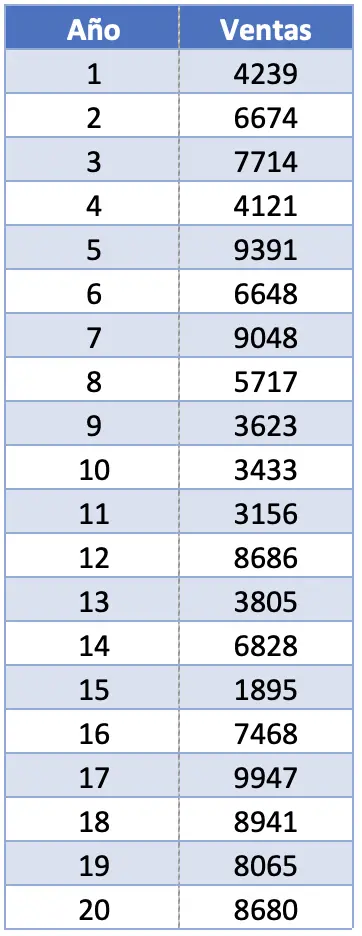
У цій вправі ми маємо 20 спостережень. Насправді загальна кількість спостережень не впливає на обчислення обсягу вибірки, оскільки нас цікавить лише найбільше та найменше значення.

Тому ми повинні використати наведену вище формулу, щоб знайти обсяг цієї статистичної вибірки.

Максимальне значення інтервалу становить 9947 проданих одиниць, а мінімальне значення – 1895. Тому нам потрібно відняти ці два значення, щоб знайти діапазон набору даних:

Це означає, що максимальна зміна продажів за останні кілька років становить 8052 одиниці. Нижче ви можете графічно побачити всі дані вправи разом із статистичним діапазоном, графік, ймовірно, допоможе вам зрозуміти значення діапазону.

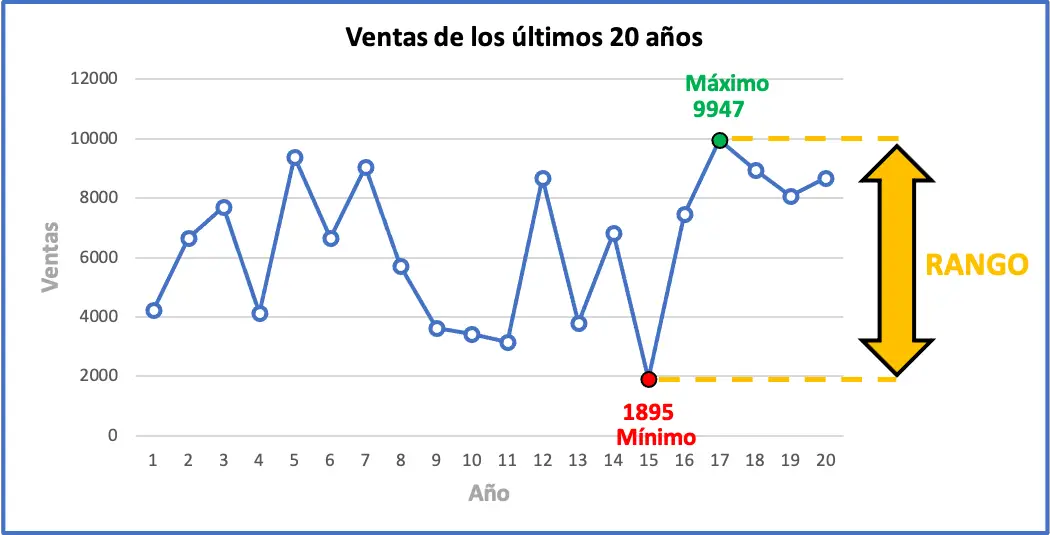
Для чого використовується статистичний діапазон?

Щоб завершити розуміння поняття екстент у статистиці, ми побачимо, для чого воно використовується та як інтерпретувати цю міру дисперсії.

У статистиці діапазон показує різницю між максимальним і мінімальним значенням набору даних. Таким чином, діапазон – це міра, яка використовується для вказівки загальної дисперсії набору даних .

Коли ви знаєте значення діапазону набору даних, ви знаєте максимальну різницю між будь-якими двома спостереженнями в цьому наборі, тому ви можете отримати уявлення про те, чи є дані розкиданими чи близькими. Загалом бажано, щоб діапазон був якомога меншим, оскільки це означає, що дисперсія незначна, а отже, розрахунки будуть більш точними.

Наприклад, діапазон може бути вимірюванням, яке дозволяє порівнювати два різні зразки, оскільки це дозволяє отримати уявлення про дисперсію зразків.

Однак слід бути обережним при інтерпретації статистичного діапазону, оскільки він може ввести в оману. Може бути так, що набір даних насправді має дуже низьку дисперсію, але якщо в межах вибірки є викид , діапазон буде дуже широким і, отже, не відображатиме належним чином дисперсію вибірки.

Крім того, для зразка, значення якого порядку десятків, мати ранг 5 не однаково, як для зразка, значення якого порядку тисяч, мати той самий ранг. Логічно, що навіть якщо обидва діапазони мають однакову кількість, перша вибірка є набагато більш розсіяною, ніж друга.

Підсумовуючи, діапазон є корисним статистичним показником для аналізу дисперсії набору даних, але для правильної інтерпретації даних необхідно також розрахувати інші показники.